数据结构（14）线性表之C++实现一元多项式相乘

最新推荐文章于 2022-11-02 18:58:22 发布
最新推荐文章于 2022-11-02 18:58:22 发布
阅读量4.6k 收藏 30
点赞数 6
分类专栏： 数据结构 文章标签： 数据结构 一元多项式 相乘 源码实现 C++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/YuYunTan/article/details/50916175
版权

导言

两个一元多项式相乘的算法，可以利用两个一元多项式相加的算法来实现，因为乘法可以分解为一系列的加法运算。

源码实现

#define   OK                    1
#define   ERROR                 0
#define   OVERFLOW             -2
#define   TRUE                  1
#define   FALSE                 0
typedef   int   Status;//为了方便算法可用性，算法的Status可以通过这里可改
#include <iostream>
#include <cstdlib>
using namespace std;
typedef struct{//项的表示，多项式的项作为LinkList的数据元素
    float coef;//系数
    int expn;//指数
}term, ElemType;//两个类型：term用于本ADT，ElemType为LinkList的数据对象名
typedef struct LNode{//节点类型
    ElemType  data;//这里表示了每一项，其指数和系数
    struct LNode *next;
}*Link, *Position;
typedef struct{//链表类型
    Link head, tail;//分别指向线性链表中的头结点和最后一个结点
    int len;//指示线性链表中数据元素的个数
}LinkList;//每一项组成一个列表
typedef LinkList polynomial;

Status InitList(LinkList *L)
{ /* 构造一个空的线性链表 */
    Link p;
    p = (Link)malloc(sizeof(LNode)); /* 生成头结点 */
    if (p)
    {
        p->next = NULL;
        (*L).head = (*L).tail = p;
        (*L).len = 0;
        return OK;
    }
    else
        return ERROR;//内存分配不够
}
Status ClearList(LinkList *L)
{ /* 将线性链表L重置为空表，并释放原链表的结点空间 */
    Link p, q;
    if ((*L).head != (*L).tail)/* 不是空表 */
    {
        p = q = (*L).head->next;
        (*L).head->next = NULL;
        while (p != (*L).tail)
        {
            p = q->next;
            free(q);
            q = p;
        }
        free(q);
        (*L).tail = (*L).head;
        (*L).len = 0;
    }
    return OK;
}
void FreeNode(Link *p)
{ /* 释放p所指结点 */
    free(*p);
    *p = NULL;
}
Status DestroyPolyn(LinkList *L)
{ /* 销毁线性链表L，L不再存在 */
    ClearList(L); /* 清空链表 */
    FreeNode(&(*L).head);
    (*L).tail = NULL;
    (*L).len = 0;
    return OK;
}
Status MakeNode(Link *p, ElemType e)
{ /* 分配由p指向的值为e的结点，并返回OK；若分配失败。则返回ERROR */
    *p = (Link)malloc(sizeof(LNode));
    if (!*p)
        return ERROR;
    (*p)->data = e;
    return OK;
}
Status InsFirst(LinkList *L, Link h, Link s) /* 形参增加L,因为需修改L */
{ /* h指向L的一个结点，把h当做头结点，将s所指结点插入在第一个结点之前 */
    s->next = h->next;
    h->next = s;
    if (h == (*L).tail) /* h指向尾结点 */
        (*L).tail = h->next; /* 修改尾指针 */
    (*L).len++;
    return OK;
}
Position GetHead(LinkList L)
{ /* 返回线性链表L中头结点的位置 */
    return L.head;
}
Status SetCurElem(Link p, ElemType e)
{ /* 已知p指向线性链表中的一个结点，用e更新p所指结点中数据元素的值 */
    p->data = e;
    return OK;
}
Status LocateElemP(LinkList L, ElemType e, Position *q, int(*compare)(ElemType, ElemType))
{ /* 若升序链表L中存在与e满足判定函数compare()取值为0的元素，则q指示L中 */
    /* 第一个值为e的结点的位置，并返回TRUE；否则q指示第一个与e满足判定函数 */
    /* compare()取值>0的元素的前驱的位置。并返回FALSE。（用于一元多项式） */
    Link p = L.head, pp;
    do
    {
        pp = p;
        p = p->next;
    } while (p && (compare(p->data, e)<0)); /* 没到表尾且p->data.expn<e.expn */
    if (!p || compare(p->data, e)>0) /* 到表尾或compare(p->data,e)>0 */
    {
        *q = pp;
        return FALSE;
    }
    else /* 找到 */
    {/* 没到表尾且p->data.expn=e.expn */
        *q = p;
        return TRUE;
    }
}
Status Remove_Polyn(LinkList *L, Link q)
{ //由于项的指数为0，删除掉已有的项
    Link p, h;
    h = L->head;
    while (h->next != q)
    {
        h = h->next;
    }
    //找到了
    if (q == L->tail)
    {//删除的如果是表尾，改变表尾
        L->tail = h;
    }
    h->next = q->next;
    free(q);
    L->len--;
    return OK;
}
int cmp(term a, term b) // CreatPolyn()的实参
{ // 依a的指数值<、=或>b的指数值，分别返回-1、0或+1
    if (a.expn == b.expn)
        return 0;
    else
        return (a.expn - b.expn) / abs(a.expn - b.expn);
}
void CreatPolyn(polynomial &p, int m)
{//输入m项的系数和指数，建立表示一元多项式的有序链表P
    InitList(&p);//初始化多项式链表
    Link h = GetHead(p);//设置头结点的数据元素
    ElemType e;//头结点设置
    Position q, s;
    e.coef = 0.0; e.expn = -1; SetCurElem(h, e);//设置头结点的元素
    for (int i = 1; i <= m; ++i)//依次输入m个非零项
    {
        cout << "第" << i << "项" << "的系数:";
        cin >> e.coef;
        cout << "第" << i << "项" << "的指数:";
        cin >> e.expn;
        if (!LocateElemP(p, e, &q, cmp))//当前链表中不存在该指数项
        {
            if (e.coef != 0)//不等于才插入
            if (MakeNode(&s, e))InsFirst(&p, q, s);//生成结点并插入链表
        }
        else//当前链表中存在该指数项,增加其系数
        {
            q->data.coef = q->data.coef + e.coef;
            //如果合起来等于0，则删除掉
            if (q->data.coef == 0)
                Remove_Polyn(&p, q);//删除掉当前节点
        }
    }
}
Status ListTraverse(LinkList L, void(*visit)(ElemType))
{ /* 依次对L的每个数据元素调用函数visit()。一旦visit()失败，则操作失败 */
    Link p = L.head->next;
    int j;
    for (j = 1; j <= L.len; j++)
    {
        visit(p->data);
        p = p->next;
    }
    cout << "\b ";
    if (L.len == 0)
        cout << "0";
    return OK;
}
void visit(ElemType e)
{
    if (e.coef > 0 && e.coef != 1 && e.expn != 0)
    {
        if (e.expn > 0)
            cout << e.coef << "x^" << e.expn << "+";
        else
            cout << e.coef << "x^(" << e.expn << ")+";
    }
    else if (e.coef < 0 && e.expn != 0)
    {
        if (e.expn > 0)
            cout << "(" << e.coef << ")x^" << e.expn << "+";
        else
            cout << "(" << e.coef << ")x^(" << e.expn << ")+";
    }
    else if (e.coef == 1 && e.expn != 0)
    {
        if (e.expn > 0)
            cout << "x^" << e.expn << "+";
        else
            cout << "x^(" << e.expn << ")+";
    }
    else if (e.expn == 0 && e.coef != 0)
        cout << e.coef << "+";
    else
        cout << "";//考虑用户输入可能有系数为0的情况，情况太多，避免万一

}
Position NextPos(Link p)
{ /* 已知p指向线性链表L中的一个结点，返回p所指结点的直接后继的位置 */
    /* 若无后继，则返回NULL */
    return p->next;
}
ElemType GetCurElem(Link p)
{ /* 已知p指向线性链表中的一个结点，返回p所指结点中数据元素的值 */
    return p->data;
}
Status DelFirst(LinkList *L, Link h, Link *q) /* 形参增加L,因为需修改L */
{ /* h指向L的一个结点，把h当做头结点，删除链表中的第一个结点并以q返回。 */
    /* 若链表为空(h指向尾结点)，q=NULL，返回FALSE */
    *q = h->next;
    if (*q) /* 链表非空 */
    {
        h->next = (*q)->next;
        if (!h->next) /* 删除尾结点 */
            (*L).tail = h; /* 修改尾指针 */
        (*L).len--;
        return OK;
    }
    else
        return FALSE; /* 链表空 */
}
Status ListEmpty(LinkList L)
{ /* 若线性链表L为空表，则返回TRUE，否则返回FALSE */
    if (L.len)
        return FALSE;
    else
        return TRUE;
}
Status Append(LinkList *L, Link s)
{ /* 将指针s(s->data为第一个数据元素)所指(彼此以指针相链,以NULL结尾)的 */
    /* 一串结点链接在线性链表L的最后一个结点之后,并改变链表L的尾指针指向新 */
    /* 的尾结点 */
    int i = 1;
    (*L).tail->next = s;
    while (s->next)
    {
        s = s->next;
        i++;
    }
    (*L).tail = s;
    (*L).len += i;
    return OK;
}
Position PriorPos(LinkList L, Link p)
{ /* 已知p指向线性链表L中的一个结点，返回p所指结点的直接前驱的位置 */
    /* 若无前驱，则返回NULL */
    Link q;
    q = L.head->next;
    if (q == p) /* 无前驱 */
        return NULL;
    else
    {
        while (q->next != p) /* q不是p的直接前驱 */
            q = q->next;
        return q;
    }
}
void OrderInsertMerge(LinkList &L, ElemType e, int(*compare)(term, term))
{ // 按有序判定函数compare()的约定，将值为e的结点插入或合并到升序链表L的适当位置
    Position q, s;
    if (LocateElemP(L, e, &q, compare)) // L中存在该指数项
    {
        q->data.coef += e.coef; // 改变当前结点系数的值
        if (!q->data.coef) // 系数为0
        { // 删除多项式L中当前结点
            s = PriorPos(L, q); // s为当前结点的前驱
            if (!s) // q无前驱
                s = L.head;
            DelFirst(&L, s, &q);
            FreeNode(&q);
        }
    }
    else // 生成该指数项并插入链表
    {
        MakeNode(&s, e); // 生成结点
        InsFirst(&L, q, s);
    }
}
void MulPolyn(polynomial &Pa,polynomial &Pb)
{
    //多项式加法:Pa = Pa*Pb,利用两个多项式的结点构成“和多项式”
    Position qa = NULL, qb = NULL;
    polynomial Pc;//临时多项式链表
    term a, b,c;
    InitList(&Pc);
    qa = GetHead(Pa);//ha和hb分别指向Pa和Pb的头结点
    if (Pa.len != 0 && Pb.len != 0)
    {
        qa = qa->next;
        while (qa)
        {
            a = GetCurElem(qa);//得到当前结点
            qb = GetHead(Pb);
            qb = qb->next;
            while (qb)
            {
                b = GetCurElem(qb);
                c.coef = a.coef*b.coef;
                c.expn = a.expn + b.expn;
                OrderInsertMerge(Pc, c, cmp);
                qb = qb->next;
            }
            qa = qa->next;
        }
        DestroyPolyn(&Pb); // 销毁Pb
        ClearList(&Pa); // 将Pa重置为空表
        Pa.head = Pc.head;
        Pa.tail = Pc.tail;
        Pa.len = Pc.len;

    }
    else if (Pa.len == 0 )
    {
        //do nothing,because The polynoimal is 0

    }
    else if (Pb.len == 0)
    {
        Pa = Pb;//把Pb赋值给Pa，让其也为0
    }
}
int main()
{
    cout << "***************************************************************************" << endl;
    cout << "                   《数据结构》<C语言版本>严蔚敏 吴伟名 编著              " << endl;
    cout << "                                编写年月2016年3月                         " << endl;
    cout << "                                 编写者:YuYunTan                          " << endl;
    cout << "                                 一元多项式相乘                           " << endl;
    cout << "***************************************************************************" << endl;

    polynomial A, B;
    cout << "请输入第一个多项式的项数为：";
    int length;
    cin >> length;
    CreatPolyn(A, length);
    //显示A出来
    cout << "PA(x) = ";
    ListTraverse(A, visit);
    cout << endl;
    //输入B
    cout << "请输入第二个多项式的项数为：";
    cin >> length;
    CreatPolyn(B, length);
    //输出B
    cout << "PB(x) = ";
    ListTraverse(B, visit);
    cout << endl;
    //假设以上输入成功
    //进行相加
    MulPolyn(A, B);
    //这时候A是合并后的结果
    cout << "PA(x)*PB(x) = ";
    ListTraverse(A, visit);
    cout << endl;
    system("pause");
    return 0;
}

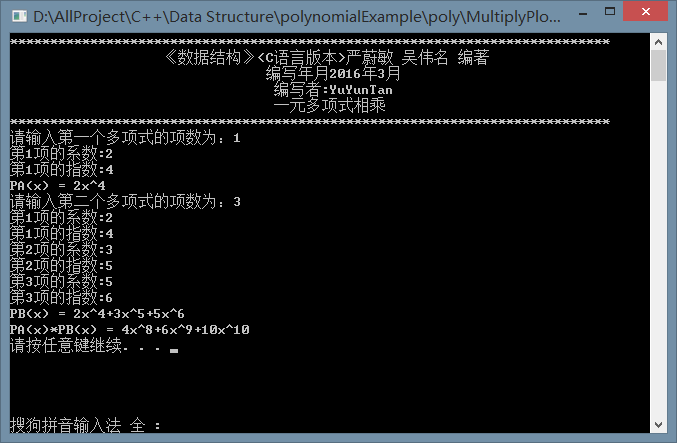
结果展示

这里写图片描述
这里写图片描述

YuYunTan
关注
专栏目录
C语言多项式加法算法实现
TechO_O的博客
09-05 332
在上述代码中，我们使用了三个指针来同时遍历两个多项式，比较它们的指数，并按照指数大小的顺序将项添加到结果多项式中。如果两个多项式的指数相同，我们将它们的系数相加，并将和添加到结果多项式中。多项式是代数学中的重要概念，它由一系列按照指数递减的项组成。在C语言中，我们可以使用数组来表示多项式，其中数组的每个元素表示一个多项式的项。接下来，我们可以定义一个函数来实现多项式的加法。通过上述代码，我们可以实现C语言中的多项式加法算法。首先，我们需要定义一个结构体来表示多项式的每个项，包括系数和指数。
线性表：两个一元多项式相乘
qq_43661234的博客
09-23 1731
热泪盈眶。。。 #include<stdio.h> #include <stdlib.h> typedef int ElemType; typedef struct LNode { float coef; //系数 int expn; //指数 struct LNode *next; }LNode, *LinkList; typedef L...
多项式相乘C++实现
09-14
两个一元多项式(降幂排列)乘法的C++实现,dev测试通过
数据结构（13）线性表之C++实现一元多项式相减
YuYunTan的专栏
03-17 3082
导言 源码导言一元多项式相减，其实是变向的一元多项式相加，只需要把减的另一个多项式，系数都取反，然后进行一元多项式相加就成。源码#define OK 1 #define ERROR 0 #define OVERFLOW -2 #define TRUE 1 #
【线性表】一元多项式相乘
weixin_34239592的博客
05-01 119
1 /* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */ 2 3 #include <stdio.h> 4 #include <stdlib.h> 5 6 typedef struct node 7 { int coef, exp; //coe...
一元多项式的乘法与加法运算（c++实现）
weixin_42403281的博客
03-07 2535
原题为PTA数据结构mooc的线性表作业第二题，题目如下： 本人是c++初学者，代码还是感觉有点费劲，大家轻拍砖。整个程序的逻辑就是四个函数组成，分别Read()函数读取输入多项式信息并形成链表，printchain()函数打印链表，chainplus()函数实现两个链表的加法，chainmult()函数实现两个链表的乘法。在设计乘法函数时，在其中也调用了加法函数进行计算。 #include&...
C++ 数据结构 一元多项式 加减乘法 链表结构实现
weixin_59629651的博客
11-02 1597
链表实现多项式，数据结构C++
数据结构与算法基础-线性表习题-两个多项式相加运算（顺序表）
”好的程序员不应该花大量时间在程序调试上，bug从一开始就不该被引入“
03-01 2078
题目 编写代码，实现两个一元多项式之间的相加，相减，相乘运算 TIP：没有除法，但是在我的代码基础上很好改，加一个判断分母为0报错即可 思路 将多项式看成线性表，每一项的指数隐藏在下标中 如果多项式连续，使用数组（顺序表）是最方便的 运算时，对应位置按顺序逐个相加/相减/相乘，直到存在空表时，将非空表内剩余元素填入即可 个人代码 王老师没有演示代码，于是我自己敲了，当作练习题 #include <iostream> using namespace std; #de
C++一元多项式的乘法运算(单链表实现)
newbie的博客
10-02 2545
题目描述:给你两个一元多项式，输出这两个一元多项式的乘积。输入格式：输入包含两行，每行一个一元多项式。每行开头一个数字n,表示该多项式非零项项数，后面有n组数字，每组数字包含两个数字，按顺序分别为该项的系数和指数。
数据结构（12）线性表之C++实现一元多项式相加
热门推荐
YuYunTan的专栏
03-17 1万+
导言 一元多项式表现形式 部分算法描述 具体实现代码 代码实现第一种 第二种代码的实现仅链表存储形式实现导言上篇文章，我们说明了一元多项式相加采取了什么形式和抽象定义数据类型定义以及实现一元多项式相加的方法，本节将用具体代码来实现一元多项式相加。一元多项式表现形式typedef struct{//项的表示，多项式的项作为LinkList的数据元素 float coef;//系数 int expn;/
数据结构+实验报告+线性表及其应用(多项式相加、相乘)等
12-15
为了实现上述功能，本实验采用了单链表作为数据结构来表示一元多项式。每个节点存储多项式中的一项的系数和指数，其中高指数的节点位于低指数节点之前，从而确保线性表按指数递增有序排列。 #### 多项式加法算法 1....
一元多项式的乘法C++
车晋强的专栏
03-05 2735
#include #include typedef struct term{  int z;   //指数  float x;     //系数  struct term *next; }term; struct term *creatlink();    //创建多项式 int cmp(int  a,int b);    //指数比较 struct term * addin(s
[线性表]一元多项式相乘
大道至简 悟在天成
05-01 766
/* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */ #include #include typedef struct node { int coef, exp; //coef：系数 exp：指数 struct node *next; //下一项 } NODE; NODE* mul
C++多项式相乘
YSL
02-23 3368
#include <iostream> using namespace std; int a[2][2]; //二维数组开的秒 int b[2][2]; int ans[25]; //用来存放系数，那么存放后所对应的下标就是指数 int main(){ for(int i=0;i<2;i++){ for(int j=0;j<2;j++){ ...
数据结构——一元多项式相乘
Begin!
10-30 1235
这个程序是转专业后写的第一个作业，除了Debug阶段有点吃力，大体还是没什么问题 void multiplication(NODE *head1,NODE *head2,NODE *head3) { NODE *p1,*p2,*p3,*p4,*p5; int coe,ex; for (p1=head1->next; p1!=NULL; p1=p1->next) {
一元多项式的加减乘除运算（c++实现）—数据结构学习
qq_29131907的博客
03-25 2648
#include<iostream> #include<stdio.h> #include<stdlib.h> using namespace std; typedef struct Node* List; struct Node { List next;//指向下一个结点 int x;//指数 int z;//系数 }; List Read() { ...
多项式相乘c++实现
05-28
实现两多项式相乘。用c++实现的。结果合并了同类项。就是没有按降幂排序。
数据结构之一元多项式相乘
cowoa1961331326
05-03 4810
#include#includetypedef struct Node{ int coef; int expn; struct Node *next;}List;List *Creat(){ List *head,*p1,*p2; p1=p2=(List *)malloc(sizeof(List)); head=NULL; scanf("%d%d",&p1
数据结构题——一元多项式相乘
qq_36805270的博客
05-01 3436
题目描述 要求采用链表形式，求两个一元多项式的乘积：h3 = h1*h2。函数原型为：void multiplication( NODE * h1, NODE * h2, NODE * h3 )。 输入： 　　输入数据为两行，分别表示两个一元多项式。每个一元多项式以指数递增的顺序输入多项式各项的系数（整数）、指数（整数）。 　　例如：1+2x+x2表示为：<1,0>,<2,1&g...
数据结构问题——一元多项式相乘
wxz1120171495的博客
10-08 7313
void multiplication(NODE *head1, NODE *head2, NODE *head3) { NODE *p1 = head3, *p2 = head3; NODE *h1 = head1-&gt;next, *h2 = head2-&gt;next; NODE *p3 = head3; while (h1)//多项式乘法运算转化为加法运算，注意双重循环控制乘...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

YuYunTan

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值