一、问题描述
为了更好地解决企业遇到的问题,本文在经典 RCPSP 的基础上做了一些延伸。本文研究的问题中将资源分为可更新资源和不可更新资源两类,其中可更新资源又分为人力资源和设备资源,为了防止人员和设备不匹配,提出了人力资源和设备资源之间的资源匹配约束。同时,人员和设备必须在各自的工作日历内执行任务,非工作时间不可安排工作,即工作日历约束。不可更新资源指成本,成本由员工工作酬劳和设备运行成本、项目拖期成本与可更新资源闲置成本组成。根据任务的具
体情况,本文将任务分为可中断任务和不可中断任务,任务中断不影响该任务执行所需的总时间和资源。
本章设定的条件假设如下:
1)项目由有限个任务组成;
2)项目中的任务存在时序约束,每个任务必须等待其紧前任务全部结束时才可以开始执行,即任何一个任务的开始执行时间不能早于其紧前任务的结束时间;
3)根据处于执行中的任务能否被中断,项目中的任务分为两种:可中断任务与不可中断任务。为了降低问题的复杂性,可中断任务只有在工作时间不连续时才可中断,比如午休、下班等,不可随意中断;
4)任务只有一种执行模式,任务的执行时间和所需资源由执行模式确定;
5)项目中的资源分为可更新资源与不可更新资源两类,其中,不可更新资源指的是成本,可更新资源中生产人员与设备资源之间有对应关系;
6)项目中的任务需要满足工作日历的约束,工作日历即企业员工的标准工作时间,不同资源的工作日历可以不同。
7)为了便于合理统计项目的执行时间,本文在计算执行时间时排除了节假日的干扰,即执行时间的计算不包含节假日。
本章研究的单模式单项目资源受限调度问题可以描述为:一个项目包含 Q 个任务,任务编号 1 ,2 , …,Q。任务 i 的持续时间为 t i 。项目中包含 M 种可更新资源与 N 种不可更新资源,任务 i 的第 m 种可更新资源使用量和第 n 种不可更新资源使用量用 r im 和 r in 表示,单位时间内可更新资源使用量上限为 r m ,项目内不可更新资源使用上限为 r n ,其中m=1,2,…,M,n=1,2,…,N,本文中可更新资源分为人力资源和设备资源两类,人力资源和设备资源要具备合理的对应关系,不会出现人员和设备不匹配的情况,不可更新资源只有成本一种,项目总成本不可以超过项目预算。所有任务的执行必须满足紧前任务约束并在工作日历内完成,不可在工作日历外执行任务,同时任务可分成可中断任务与不可中断任务两种,任务中断不影响该任务执行所需的总时间和资源。在这由 Q 个任务组成的项目中,在满足紧前关系约束、资源约束、资源匹配约束和工作日历约束的前提下,通过安排各项任务的执行顺序、资源分配和执行时间,最小化项目执行时间,使有限的资源得到合理利用。
二、基于改进遗传算法的单模式单项目资源受限调度问题模型求解
2.1 染色体编码设计
针对所研究的单模式单项目资源受限调度问题的特点,本章提出用双层实数编码。染色体由两层实数组成,第一层表示任务调度顺序,该层中每个基因用任务编号 i 表示,i= 1 ,2 ,…… , Q ,第二层表示第一层对应的任务能否中断,若对应任务为可中断任务,则表示为 0,否则为 1。
在生成任务调度顺序时,需要考虑任务的紧前关系约束,编码流程如下:
Step1:搜索所有任务,得到每个任务的紧前任务数集合 E,任务 i 的紧前任务数用 E i 表示;
Step2:判断任务列表中包含的任务数 n 是否等于任务总数 Q,若是转 Step4,否则转 Step3;
Step3:在紧前任务数集合 E 中找到紧前任务数 E i 为 0 的任务编号,在这些编号中随机选择一个任务放入任务列表,并将该任务的所有紧后任务的紧前任务数减 1,同时将该任务从紧前任务数集合 E 中移除,转 Step2:
Step4:输出任务列表。
用python进行编码,代码如下,代码思路比较简单,基本思路已写在代码注释中:
import random
import numpy as np
class Encode:
def __init__(self,Task,Qutity,Interrupt):
self.Task = Task
self.Qutity = Qutity
self.Interrupt = Interrupt
def Chromosome1(self):
chromosome1 = [] # 任务列表,染色体1
for a in range(self.Qutity):
Ei_0 = [] # 紧前任务数为0的任务编号集合
for key, Ei in self.Task.items(): # 搜索所有任务(遍历字典中的key和value)
# Ei即为每个任务的紧前任务集合
Ei_number = len(Ei) - 1 # 每个任务的紧前任务数量,减1是因为所有都包含了0任务
if Ei_number == 0:
Ei_0.append(key)
random.shuffle(Ei_0)
random_Ei_0 = Ei_0[0] # 随机取一个 = 随机打乱list取第一个
chromosome1.append(random_Ei_0)
for key, Ei in self.Task.items():
if random_Ei_0 in Ei:
Ei.remove(random_Ei_0)
del self.Task[random_Ei_0]
return chromosome1
def Chromosome(self):
chromosome1 = self.Chromosome1()
chromosome2 = []
for i in chromosome1:
b = self.Interrupt[i]
chromosome2.append(b)
chromosome = np.hstack((chromosome1,chromosome2))
return chromosome代码测试:
假设,某订单分解成 11 个任务。任务网络图如图 2.1 所示,任务紧前关系表如表 2.1 所示。

图2.1 任务网络图
图2.1 任务紧前关系表
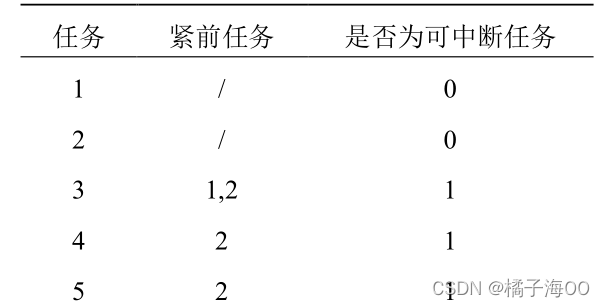

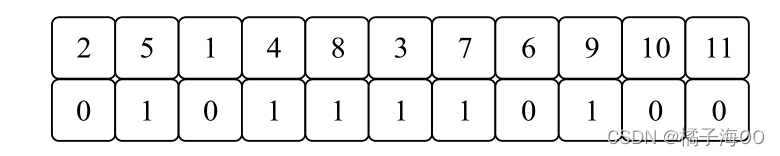
预期编码方案:
测试代码如下:
def main():
Task = {1:[0],2:[0],3:[0,1,2],4:[0,2],5:[0,2],6:[0,3,4],7:[0,4],8:[0,5],9:[0,8],10:[0,5,9],11:[0,6,7,10]}
Interrupt = {1:0,2:0,3:1,4:1,5:1,6:0,7:1,8:1,9:1,10:0,11:0}
Qutity = 11
t = Encode(Task,Qutity,Interrupt)
print(t.Chromosome())
if __name__ == '__main__':
main()结果:
[ 2 4 5 1 3 8 9 6 10 7 11 0 1 1 0 1 1 1 0 0 1 0]







 本文探讨了资源受限的单模式单项目调度问题,区分了可更新资源(如人力资源和设备资源)与不可更新资源(成本),并引入了资源匹配和工作日历约束。为了解决这一问题,提出了基于改进遗传算法的解决方案,通过双层实数编码来表示任务调度顺序和中断属性。编码过程遵循任务的紧前关系,以生成满足约束的可行调度。
本文探讨了资源受限的单模式单项目调度问题,区分了可更新资源(如人力资源和设备资源)与不可更新资源(成本),并引入了资源匹配和工作日历约束。为了解决这一问题,提出了基于改进遗传算法的解决方案,通过双层实数编码来表示任务调度顺序和中断属性。编码过程遵循任务的紧前关系,以生成满足约束的可行调度。
















 1784
1784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








