拉格朗日乘子法（有约束优化问题）

拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。前提是：只有当目标函数为凸函数时，使用这两种方法才保证求得的是最优解。

对于无约束最优化问题，有很多经典的求解方法，参见无约束最优化方法。

---

拉格朗日乘子法

先来看拉格朗日乘子法是什么，再讲为什么。

$$\min\;f(x)\tag{1}$$ $$s.t.\;h_i(x)=0\;\;\;i=1,2 \ldots n \tag{2}$$

这里(1)是目标函数，(2)是约束条件。s.t. = subject to，受限制于。利用拉格朗日乘子法，该问题可以转化为：

$$\min[f(x)+\sum_{i=1}^{n}\lambda_{i}h_{i}(x)] \tag{3}$$

其中$\lambda_{i} \not=0$，称为拉格朗日乘子。

下面就是求式(3)的最优值，可以通过对式(3)各个参数求导取零，联立等式进行求取，这个在高等数学里面有讲，但是没有讲为什么这么做就可以，下面将简要介绍其思想。

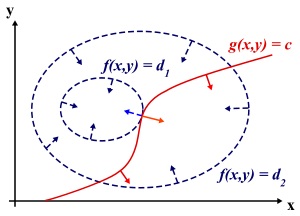
为什么要这么求能得到最优值？先说拉格朗日乘子法，设想我们的目标函数$z=f(x)$，$x$是向量，$z$取不同的值，相当于可以投影在$x$构成的平面（曲面）上，即成为等高线，如下图，目标函数是$f(x, y)$，这里$x$是标量，虚线是等高线，现在假设我们的约束$g(x)=0$，$x$是向量，在$x$构成的平面或者曲面上是一条曲线，假设$g(x)$与等高线相交，交点就是同时满足等式约束条件和目标函数的可行域的值，但肯定不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值，如下图所示，即等高线和目标函数的曲线在该点的法向量必须有相同方向，所以最优值必须满足：$f(x)$的梯度 $= a* g(x)$的梯度， a <script type="math/tex" id="MathJax-Element-883">a</script>是常数，表示左右两边同向。这个等式就是式(3)对参数求导的结果。