奇异值分解SVD

一 特征分解

线性代数中有个定理：实对称矩阵A（A=A^T）一定可以相似对角化于对角矩阵Σ,且一定存在一个正交矩阵Q，通过对A进行正交变换使得其变换为对角阵，即下述公式成立：

上述公式中，Q的列向量是矩阵A的特征向量，λ是矩阵A的特征值。将矩阵A分解为特征向量矩阵Q（也是正交矩阵)和特征值矩阵Σ的过程叫作特征分解。很显然，这样的分解是具有局限性的：

• 分解的对象必须是方阵
• 分解的对象必须是对称的

那么，如果给出的矩阵A是m*n阶的一般矩阵，是否能对其进行特征分解？
答案是可以的，奇异值分解SVD就是实现一般矩阵的分解的。

二 奇异值分解（SVD）

1.SVD概述

SVD提供两组基向量（左奇异向量和右奇异向量）对数据矩阵A作行放缩和列放缩，非常适用于没有均值中心化（各数减去所在列的平均值）的稀疏数据（稀疏矩阵）。SVD方便地提供了矩阵分解和基表示以及基的重要程度（奇异值越大，越重要），被誉为“线性代数的绝对亮点”。SVD定义：对于一个m*n阶实数矩阵A，可以将其分解为如下形式：

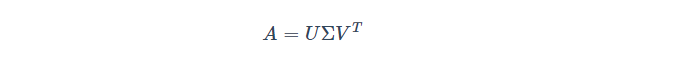
上述公式中，U是一个m×m的正交矩阵（UU^T =E），其正交列称为左奇异向量；V是一个n×n的正交矩阵（VV^T =E），其正交列称为右奇异向量；Σ是一个包含奇异值的m*n的对角矩阵(注意，Σ不一定是方阵。长方形的矩阵只要其只有Σii元素是非0的，也称为对角阵)。

2.SVD性质

• U中的列(左奇异向量)是AA^T 的正交特征向量。因为：L=AA^T =UΣ(V^T V)Σ^TU^T =UΣΣ^TU^T

• V中的列(右奇异向量)是A^T A的正交特征向量。因为：R=A^T A=VΣ^T(U^TU)ΣV^T = VΣ^T ΣV^T

• ΣΣ^T 和Σ^T Σ虽是不同的对角阵( ΣΣ^T是m×m阶的，Σ^TΣ是 n×n阶的)，但其主对角元素都是奇异值的平方。如下图所示：
  

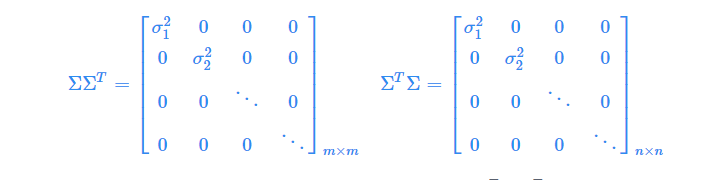
• 一般性地，将Σ的奇异值按递减排列，U和V与之对应

• SVD可以消除噪声： 在实际应用中，只有前K(k<<n)个奇异值相对较大，其余的都非常小可以忽略。那么，我们选择U的前k列，V^T 的前k行，还有Σ前K个奇异值。产生原始数据A的近似矩阵：A≈Uk·Σk·Vk^T 。

• SVD可以用来数据降维：Vk中的列(前k个右奇异向量)可以表示为数据集进行列规约的k维基座标，即A’=A·Vk=Uk·Σk。Uk中的列（前k个左奇异向量）可以表示为数据集进行行规约的k维基座标，即(A^T )’=A^T ·Uk=Vk·Σk。

3.SVD计算实例

给出一个数学题计算的实例：

三 SVD实现

1.算法描述

该算法是从纯数学计算的角度去实现SVD的，算法过程如下：

• 输入m×n矩阵A
• 计算L=AA^T 并进行特征分解，得左奇异矩阵U 和对角矩阵Λ=ΣΣ^T
• Λ对角元素开根号得奇异值，生成m×n奇异值矩阵S
• 计算R=A^T A并进行特征分解，得右奇异矩阵V
• U,S,V均按照奇异值降序排列
• 找到前k个最大值
• 计算近似矩阵A1=Uk·Sk·Vk^T
• 输出A1,U,S,V

显然这个算法的时间复杂度为特征分解的时间复杂度O(n³)。当然还有效率更高的算法，有兴趣者可以自行补充，本人不会。

2.python实现

看代码：