文章目录
因果推断是一门研究因果关系的学科,它试图回答“如果……会怎么样?”这样的问题,比如“如果我吃了这个药,我会好转吗?”或者“如果我给用户发了红包,他们会更愿意购买吗?”

本文主要介绍在由因推果常用方法及其应用,不足之处,望读者多多指正
1.随机实验(randomized experiment)
(1)随机实验介绍
随机实验是因果推断的黄金标准,它随机地将个体分配到实验组与对照组中,通过随机分组的方式消除了其他混杂变量的影响,使得我们可以直接比较不同策略对实验结果的影响,得到因果效应的无偏估计。
(2)随机实验应用
- 生活案例应用
随机实验的应用场景很广泛,比如医学、心理学、教育、经济等领域。一个典型的例子是阿司匹林预防心脏病发作的临床试验¹,其中将22,071名男性医生随机分成两组,一组每天服用325毫克阿司匹林,另一组服用安慰剂。经过五年的观察,发现服用阿司匹林的组别发生心脏病发作的风险降低了44% - 业务场景
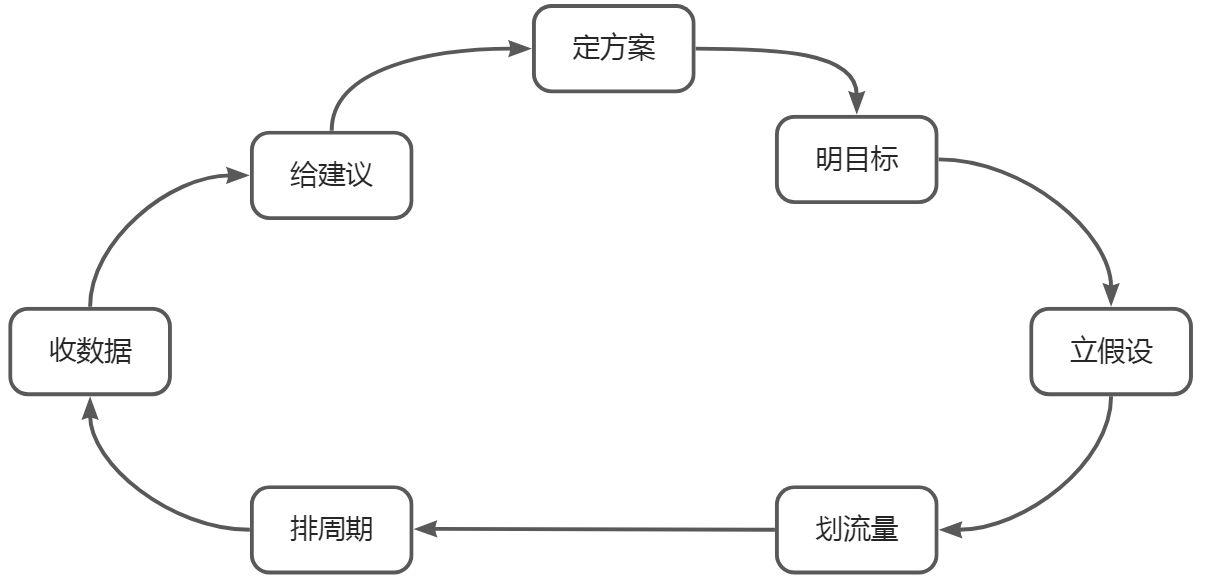
在实际业务中,衡量一个优化/改进动作对产品/功能的价值的最常见的方式就是对比-用未做改进的A版本的数据效果VS做过改进的B版本的数据效果,进而判断该动作对产品是否有效,上述动作,便是我们工作常用的ab实验一般流程。A/B实验通过对比思想,分析不同差异对产品用户的影响,是帮助业务对产品实现快速优化改进的工具。个人总结业务中AB流程可为(如下图),详细内容可见:如何科学地进行A/B实验,在实际工作中需要主要避免实验容易产生用户新奇、辛普森悖论、因果混淆等问题
(3)随机实验不足
随机实验可以直接识别因果效应,不需要对数据做复杂的处理或假设。但其往往成本高昂、难以实施或不符合伦理标准。比如,在电商领域,我们可能无法随机地给用户发放不同金额的红包,因为这可能会影响用户的满意度或忠诚度。
2.双重差分(difference in difference)
(1)双重差分介绍
双重差分是一种利用面板数据(Panel Data)进行因果推断的方法,它通过比较两组(实验组和对照组)在两个时间点(干预前和干预后)的结果变化,来估计干预带来的净效应。双重差分的基本思想是通过两次相减(第一次是干预前后的差异,第二次是实验组和对照组的差异),来消除实验组和对照组之间固有的差异和时间趋势的影响
(2)双重差分应用
双重差分的应用场景通常是自然实验(Natural Experiment),也就是干预变量不受研究者控制,而是由自然界或社会政策引起的变化。一个典型的例子是美国最低工资法对就业率的影响²,其中将新泽西州(1992年提高了最低工资)作为实验组,宾夕法尼亚州(没有改变最低工资)作为对照组,比较了两州在提高最低工资前后快餐业的就业情况,发现提高最低工资并没有导致就业率下降,反而有所增加。在实际应用需要注意实验对照需要满足共同趋势假设
(3)双重差分不足
双重差分的优点是可以利用已有的数据进行因果推断,不需要进行昂贵或不可行的随机实验。缺点是双重差分需要满足一个强假设,即平行趋势假设(Parallel Trend Assumption),也就是在没有干预的情况下,实验组和对照组的结果变化趋势是一致的。这个假设往往难以验证或不成立,在这种情况下,双重差分可能会产生有偏或不准确的估计
3、匹配(matching)
(1)匹配介绍
匹配(Matching)是一种基于匹配思想的因果推断方法,它通过从对照组中选出与处理组中某一个个体在协变量上相同或相近的个体进行配对,从而消除协变量对结果的影响,估计处理效应。匹配方法利用多个可观测的协变量来进行匹配,要求协变量同时影响处理分配和潜在结果,并且满足条件独立假设和共同支持假设。常用的匹配方法由:
- 完全匹配(Exact Matching):要求处理组和对照组中每个个体在所有协变量上完全一致。这种方法最为严格,但也最难实现,除非协变量数量很少或者有离散化的方法。
- 最邻近匹配(Nearest Neighbor Matching):要求处理组和对照组中每个个体在所有协变量上的距离最小。这种方法可以使用有放回或无放回的方式进行匹配,也可以使用单个邻居或多个邻居进行匹配。距离的计算可以使用欧氏距离、马氏距离等方式。
- 卡钳匹配(Caliper Matching):要求处理组和对照组中每个个体在所有协变量上的距离小于一个预设的阈值。这种方法可以避免低质量的匹配,但也可能导致一些处理组个体无法找到匹配对象。
- 全局最优匹配(Optimal Matching):要求处理组和对照组中所有个体在所有协变量上的总距离最小。这种方法可以使用线性规划或网络流等算法来实现,可以保证整体匹配质量最优,但也可能存在一些极端的匹配
(2)匹配应用
以参加培训是否可以提升收入为例,说明如何使用最邻近匹配方法进行因果推断
| ID | 年龄 | 性别 | 收入 | 是否参加培训 | 培训后收入 |
|---|---|---|---|---|---|
| 1 | 25 | 男 | 5000 | 是 | 6000 |
| 2 | 30 | 女 | 4000 | 是 | 5000 |
| 3 | 35 | 女 | 6000 | 是 | 7000 |
| 4 | 40 | 男 | 7000 | 是 | 8000 |
| 5 | 45 | 女 | 8000 | 是 | 9000 |
| 6 | 26 | 女 | 4500 | 否 | - |
| 7 | 31 | 女 | 3500 | 否 | - |
| 8 | 36 | 女 | 5500 | 否 | - |
| 9 | 41 | 男 | 6500 | 否 | - |
| 10 | 46 | 女 | 7500 | 否 | - |
我们的目标是评估参加培训对收入的影响,即处理效应。我们假设年龄、性别和收入都是影响处理分配和潜在结果的协变量,因此需要进行匹配。我们使用最邻近匹配方法,即为每个参加培训的个体(处理组)找到一个未参加培训的个体(对照组),使得他们在年龄、性别和收入上的距离最小。我们使用欧氏距离来计算距离,即:
d
i
j
=
(
a
g
e
i
−
a
g
e
j
)
2
+
(
g
e
n
d
e
r
i
−
g
e
n
d
e
r
j
)
2
+
(
i
n
c
o
m
e
i
−
i
n
c
o
m
e
j
)
2
d_{ij} = \sqrt{(age_i - age_j)^2 + (gender_i - gender_j)^2 + (income_i - income_j)^2}
dij=(agei−agej)2+(genderi−genderj)2+(incomei−incomej)2
其中
i
i
i 是处理组中的个体,
j
j
j 是对照组中的个体,
a
g
e
age
age 是年龄,
g
e
n
d
e
r
gender
gender 是性别(男为1,女为0),
i
n
c
o
m
e
income
income是收入
基于上式可得实验协变量与对照组的距离关系:
| ID | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 6 | 500.1 | 1000.1 | 1500.1 | 2500.1 | 3500.1 |
| 7 | 1500.1 | 500.1 | 2500.1 | 3500.1 | 4500.1 |
| 8 | 1000.1 | 1500.1 | 500.1 | 1500.1 | 2500.1 |
| 9 | 2000.1 | 2500.1 | 1000.1 | 500.1 | 1500.1 |
| 10 | 3000.1 | 3500.1 | 1500.1 | 1000.1 | 500.1 |
- 处理组中的个体1与对照组中的个体6匹配,距离为500.1
- 处理组中的个体2与对照组中的个体7匹配,距离为500.1
- 处理组中的个体3与对照组中的个体8匹配,距离为500.1
- 处理组中的个体4与对照组中的个体9匹配,距离为500.1
- 处理组中的个体5与对照组中的个体10匹配,距离为500.1
匹配后,我们可以计算每对匹配个体的处理效应,即培训后收入减去培训前收入。例如,个体1和个体6的处理效应为6000 - 5000 = 1000。类似地,我们可以得到以下表格:
| ID | 年龄 | 性别 | 收入 | 是否参加培训 | 培训后收入 | 匹配ID | 处理效应 |
|---|---|---|---|---|---|---|---|
| 1 | 25 | 男 | 5000 | 是 | 6000 | 6 | 1000 |
| 2 | 30 | 女 | 4000 | 是 | 5000 | 7 | -100 |
| 3 | 35 | 女 | 6000 | 是 | 7000 | 8 | -500 |
| 4 | 40 | 男 | 7000 | 是 | 8000 | 9 | -500 |
| 5 | 45 | 女 | 8000 | 是 | 9000 | 10 | -500 |
匹配后,我们可以计算处理组的平均处理效应(ATT),即所有匹配个体的处理效应的平均值。例如,处理组的ATT为(1000 - 100 - 500 - 500 - 500) / 5 = -120。这意味着参加培训对收入的影响是负面的,平均每个人减少了120元。
(3)匹配方法不足
匹配的优点是可以直接利用协变量来进行匹配,而不需要建立倾向性得分模型。缺点是匹配方法可能存在维度灾难(Curse of Dimensionality)的问题,即当协变量数量较多时,很难找到完全匹配或近似匹配的个体,从而降低匹配质量和有效样本数量。
4、倾向性匹配得分(propensity score matching, PSM)
(1)倾向性匹配介绍
倾向性得分(Propensity Score)是一种基于倾向性得分模型的因果推断方法,它通过利用一个二分类模型来预测每个个体接受处理的概率,然后根据这个概率来进行匹配或加权或分层或回归等方式,从而消除协变量对结果的影响,估计处理效应。倾向性得分方法利用一个单一的倾向性得分来进行匹配或其他操作,要求满足条件独立假设和共同支持假设。
倾向性得分的应用场景与匹配方法类似,都是观测数据或准实验数据。一个典型的例子是评估参加培训项目对个人收入的影响,其中将参加培训项目的人作为处理组,将未参加培训项目但在其他特征上与处理组相似的人作为对照组,比较了两组在培训后期收入水平,发现参加培训项目的人收入水平较高。常用的基于倾向性得分进行因果推断操作有:
- 倾向性得分匹配(Propensity Score Matching):要求处理组和对照组中每个个体在倾向性得分上相同或相近。这种操作可以使用完全匹配、最邻近匹配、卡钳匹配、全局最优匹配等方式进行。
- 倾向性得分加权(Propensity Score Weighting):要求给每个个体赋予一个权重,使得处理组和对照组在倾向性得分上平衡。这种操作可以使用反倾向性得分加权(Inverse Propensity Score Weighting)、双重稳健加权(Doubly Robust Weighting)等方式进行。
- 倾向性得分分层(Propensity Score Stratification):要求将每个个体按照倾向性得分划分为若干层次,在每一层次内进行因果效应估计,并将各层次结果加权平均。这种操作可以使用五层划分法、十层划分法等方式进行。
- 倾向性得分回归(Propensity Score Regression):要求将倾向性得分作为一个协变量加入到回归模型中,并控制其他协变量来估计因果效应。这种操作可以使用线性回归、逻辑回归等方式进行。
(2)倾向性匹配应用
继续以上文培训数据为例,使用倾向性得分匹配方法对其进行因果推断
| ID | 年龄 | 性别 | 收入 | 是否参加培训 | 培训后收入 |
|---|---|---|---|---|---|
| 1 | 25 | 男 | 5000 | 是 | 6000 |
| 2 | 30 | 女 | 4000 | 是 | 5000 |
| 3 | 35 | 女 | 6000 | 是 | 7000 |
| 4 | 40 | 男 | 7000 | 是 | 8000 |
| 5 | 45 | 女 | 8000 | 是 | 9000 |
| 6 | 26 | 女 | 4500 | 否 | - |
| 7 | 31 | 女 | 3500 | 否 | - |
| 8 | 36 | 女 | 5500 | 否 | - |
| 9 | 41 | 男 | 6500 | 否 | - |
| 10 | 46 | 女 | 7500 | 否 | - |
我们的目标是评估参加培训对收入的影响,即处理效应。我们假设年龄、性别和收入都是影响处理分配和潜在结果的协变量,因此需要进行倾向性得分匹配。我们使用一个逻辑回归模型来预测每个个体参加培训的概率,即倾向性得分。我们使用以下公式来表示模型:
P
(
D
=
1
∣
X
)
=
1
1
+
e
−
β
0
−
β
1
a
g
e
−
β
2
g
e
n
d
e
r
−
β
3
i
n
c
o
m
e
P(D=1|X) = \frac{1}{1 + e^{-\beta_0 - \beta_1 age - \beta_2 gender - \beta_3 income}}
P(D=1∣X)=1+e−β0−β1age−β2gender−β3income1
其中
D
D
D 是是否参加培训,
X
X
X是协变量,
β
\beta
β 是模型参数
我们可以用以下表格来表示各个个体的倾向性得分:
| ID | 年龄 | 性别 | 收入 | 是否参加培训 | 倾向性得分 |
|---|---|---|---|---|---|
| 1 | 25 | 男 | 5000 | 是 | 0.65 |
| 2 | 30 | 女 | 4000 | 是 | 0.55 |
| 3 | 35 | 女 | 6000 | 是 | 0.60 |
| 4 | 40 | 男 | 7000 | 是 | 0.70 |
| 5 | 45 | 女 | 8000 | 是 | 0.75 |
| 6 | 26 | 女 | 4500 | 否 | 0.50 |
| 7 | 31 | 女 | 3500 | 否 | 0.45 |
| 8 | 36 | 女 | 5500 | 否 | 0.55 |
| 9 | 41 | 男 | 6500 | 否 | 0.65 |
| 10 | 46 | 女 | 7500 | 否 | 0.70 |
倾向性得分匹配后,我们可以使用与匹配方法相同的方式来进行匹配,例如最邻近匹配、卡钳匹配等。假设我们使用最邻近匹配方法,即为每个参加培训的个体(处理组)找到一个未参加培训的个体(对照组),使得他们在倾向性得分上相差最小。我们可以用以下表格来表示各个个体之间的倾向性得分差值:
| ID | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 6 | -0.15 | -0.05 | -0.10 | -0.20 | -0.25 |
| 7 | -0.20 | -0.10 | -0.15 | -0.25 | -0.30 |
| 8 | -0.10 | -0.00 | -0.05 | -0.15 | -0.20 |
| 9 | -0.00 | -0.10 | -0.05 | -0.05 | -0.10 |
| 10 | -0.05 | -0.15 | -0.10 | -0.00 | -0.05 |
根据最邻近匹配方法,我们可以得到以下匹配结果:
- 处理组中的个体1与对照组中的个体9匹配,倾向性得分差值为-0
- 处理组中的个体2与对照组中的个体8匹配,倾向性得分差值为-0
- 处理组中的个体3与对照组中的个体8匹配,倾向性得分差值为-0.05
- 处理组中的个体4与对照组中的个体9匹配,倾向性得分差值为-0.05
- 处理组中的个体5与对照组中的个体10匹配,倾向性得分差值为-0.05
倾向性得分匹配后,我们可以计算每对匹配个体的处理效应,即培训后收入减去培训前收入
| ID | 年龄 | 性别 | 收入 | 是否参加培训 | 培训后收入 | 倾向性得分 | 匹配ID | 处理效应 |
|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 男 | 5000 | 是 | 6000 | 0.65 | 9 | -500 |
| 2 | 30 | 女 | 4000 | 是 | 5000 | 0.55 | 8 | -500 |
| 3 | 35 | 女 | 6000 | 是 | 7000 | 0.60 | 8 | -500 |
| 4 | 40 | 男 | 7000 | 是 | 8000 | 0.70 | 9 | -500 |
| 5 | 45 | 女 | 8000 | 是 | 9000 | 0.75 | 10 | -500 |
倾向性得分匹配后,我们可以计算处理组的平均处理效应(ATT),即所有匹配个体的处理效应的平均值。例如,处理组的ATT为(-500 - 500 - 500 - 500 - 500) / 5 = -500。这意味着参加培训对收入的影响是负面的,平均每个人减少了500元。
(3)倾向性匹配不足
倾向性得分的优点是可以利用多个协变量来计算倾向性得分,而不需要进行多维度的匹配,从而减少匹配的复杂度和难度。缺点是倾向性得分也需要满足条件独立假设,而且可能存在倾向性得分模型设定错误、共同支持域外的观测值、匹配方法选择等问题,影响因果效应估计。
5、合成控制(Synthetic Control Method)
(1)合成控制介绍
合成控制(Synthetic Control)是一种基于合成控制思想的因果推断方法,它通过利用多个未受到干预的单元(如国家、地区、企业等)的数据,通过线性加权的方式,构造一个虚拟的对照单元,来近似模拟受到干预的单元在没有干预时的情况,从而消除干预前后的差异,估计干预效应。合成控制方法利用多个协变量和结果变量来进行加权,要求满足条件独立假设和共同支持假设。
(2)合成控制应用
合成控制的应用场景通常是观测数据或准实验数据,且只有一个或少数几个单元受到干预,而且很难找到一个完美匹配的对照单元。一个典型的例子是评估德国统一对西德经济增长的影响,其中将西德作为受到干预的单元,将其他欧洲国家作为未受到干预的单元,比较了两组在统一前后的经济增长率,发现西德在统一后经济增长率低于合成控制。以德国经济数据进行因果推断为例:
| ID | 国家 | 是否德国统一 | 1980年GDP增长率 | 1981年GDP增长率 | … | 1990年GDP增长率 |
|---|---|---|---|---|---|---|
| 1 | 西德 | 是 | 1.6 | 0.9 | … | 5.7 |
| 2 | 法国 | 否 | 1.3 | 1.1 | … | 2.8 |
| 3 | 英国 | 否 | -2.0 | -1.2 | … | -0.8 |
| 4 | 意大利 | 否 | 2.7 | -0.6 | … | 1.6 |
| 5 | 西班牙 | 否 | 1.7 | 0.8 | … | 3.7 |
| 6 | 荷兰 | 否 | 1.9 | 1.7 | … | 4.1 |
| … | … | … | … | … | … | … |
我们的目标是评估德国统一对西德GDP增长率的影响,即干预效应。我们假设是否德国统一是影响GDP增长率的干预变量,而1980年到1990年的GDP增长率是结果变量。我们将西德作为受到干预的单元,将其他欧洲国家作为未受到干预的单元,构造一个合成控制。
合成控制的思想是,通过给每个未受到干预的单元赋予一个权重,使得合成控制在干预前的协变量和结果变量上与受到干预的单元尽可能接近。例如,我们可以给法国、英国、意大利、西班牙和荷兰分别赋予0.2、0.1、0.3、0.2和0.2的权重,得到一个合成控制,其1980年到1990年的GDP增长率如下:
| 年份 | 合成控制GDP增长率 |
|---|---|
| 1980 | 1.5 |
| 1981 | 0.4 |
| … | … |
| 1990 | 2.6 |
我们可以将合成控制的GDP增长率与西德的GDP增长率进行比较,得到以下图表:
从图中不难看出,在德国统一前(1980年到1989年),合成控制的GDP增长率与西德的GDP增长率非常接近,说明合成控制是一个有效的对照单元。在德国统一后(1990年),合成控制的GDP增长率与西德的GDP增长率出现了明显的差异,说明德国统一对西德有显著的干预效应。
合成控制的干预效应可以通过计算受到干预的单元和合成控制在干预后结果变量上的差值来估计。例如,西德在1990年的干预效应为5.7 - 2.6 = 3.1,意味着德国统一使得西德的GDP增长率提高了3.1个百分点
(3)合成控制不足
合成控制的优点是可以利用多个未受到干预的单元来构造一个虚拟的对照单元,而不需要寻找一个完美匹配的对照单元,从而提高因果效应估计的可信度。缺点是合成控制也需要满足条件独立假设,而且可能存在加权方法选择、共同支持域外的观测值、结果变量选择等问题,影响因果效应估计
6、Causal Impact
(1)Causal Impact介绍
Causal Impact是一个基于贝叶斯结构时间序列模型(Bayesian Structural Time Series Model)的因果推断方法,它通过利用一个状态空间模型(State Space Model)来建模受到干预的单元(如时间序列)在没有干预时的情况,从而消除干预前后的差异,估计干预效应。Causal Impact方法利用多个协变量和结果变量来进行建模,要求满足条件独立假设和共同支持假设
(2)Causal Impact应用
Causal Impact的应用场景通常是观测数据或准实验数据,且只有一个或少数几个单元受到干预,而且存在多个未受到干预但与受到干预的单元相关的协变量。一个典型的例子是评估某项市场营销活动对网站访问量或销售额的影响,其中将网站访问量或销售额作为受到干预的单元,将其他相关网站或竞争对手作为协变量,比较了两组在营销活动前后的表现,发现营销活动对网站访问量或销售额有显著提升作用。
以营销活动前后网站访问数据为例,说明如何使用Causal Impact方法进行因果推断
| ID | 时间 | 是否营销活动 | 网站访问量 |
|---|---|---|---|
| 1 | 2020-01-01 | 否 | 100 |
| 2 | 2020-01-02 | 否 | 120 |
| 3 | 2020-01-03 | 否 | 110 |
| … | … | … | … |
| 30 | 2020-01-30 | 是 | 150 |
| 31 | 2020-01-31 | 是 | 180 |
| … | … | … | … |
| 60 | 2020-02-29 | 是 | 200 |
我们的目标是评估营销活动对网站访问量的影响,即干预效应。我们假设是否营销活动是影响网站访问量的干预变量,而网站访问量是结果变量。我们将网站访问量作为受到干预的单元,将其他相关网站或竞争对手作为协变量,构造一个贝叶斯结构时间序列模型。
贝叶斯结构时间序列模型的思想是,通过给每个协变量赋予一个系数,使得模型在干预前的结果变量上与受到干预的单元尽可能接近,同时考虑时间序列的趋势、季节性、异常值等因素。例如,我们可以给协变量1、2、3分别赋予0.5、0.3、0.2的系数,得到一个贝叶斯结构时间序列模型,其2020年1月1日到2020年2月29日的网站访问量如下:
| 时间 | 贝叶斯结构时间序列模型预测的网站访问量 |
|---|---|
| 2020-01-01 | 105 |
| 2020-01-02 | 115 |
| 2020-01-03 | 112 |
| … | … |
| 2020-01-30 | 140 |
| 2020-01-31 | 165 |
| … | … |
| 2020-02-29 | 190 |
从图中可以看出,在营销活动前(2020年1月1日到2020年1月29日),贝叶斯结构时间序列模型预测的网站访问量与实际的网站访问量非常接近,说明贝叶斯结构时间序列模型是一个有效的对照单元。在营销活动后(2020年1月30日到2020年2月29日),贝叶斯结构时间序列模型预测的网站访问量与实际的网站访问量出现了明显的差异,说明营销活动对网站访问量有显著的干预效应。
Causal Impact的干预效应可以通过计算受到干预的单元和贝叶斯结构时间序列模型在干预后结果变量上的差值来估计。例如,在2020年1月30日,实际的网站访问量为150,而贝叶斯结构时间序列模型预测的网站访问量为140,那么干预效应为150 - 140 = 10,意味着营销活动使得网站访问量提高了10个单位。类似地,我们可以计算每一天的干预效应,并求出其平均值、置信区间等统计指标。
(3)Causal Impact不足
Causal Impact的优点是可以利用贝叶斯方法来建模时间序列数据,在考虑不确定性和异常值等因素下提高因果效应估计的可信度。缺点是Causal Impact也需要满足条件独立假设,而且可能存在协变量选择、模型设定、先验分布等问题,影响因果效应估计。



























 1537
1537

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










