文章目录
本篇对搜索二叉树常见的面试OJ进行了总结,方便对常见的数据结构使用方法进行总结
1.根据二叉树创建字符串
✏️题目描述:

✏️示例:

传送门: 根据二叉树创建字符串
题解:

观察示例可以知道,无论是左为空还是左为不为空,都要添加括号,所以直接递归下去,右分支则可以根据情况省略括号
💻代码实现:
class Solution
{
public:
string tree2str(TreeNode* root)
{
if (root == nullptr)
{
return " ";
}
string str = to_string(root->val);
if (root->left || root->right)
{
str += '(';
str += tree2str(root->left);
str += ')';
}
if (root->right)
{
str += '(';
str += tree2str(root->right);
str += ')';
}
return str;
}
};
2.二叉树的层序遍历 Ⅰ
✏️题目描述:

✏️示例:

传送门: 二叉树的层序遍历 Ⅰ
题解:
据题意可知,需要将数据存储在一个二维数组,这里是个典型的层序遍历,即 BFS(广度优先遍历),之前在数据结构部分用C语言进行了初步解析实现,这里用 C++ 更普世的方法来实现 BFS
💻细节问题:
注意二维数组的元素是一维数组,每次 push 要 push 到下一层,vv.back() 表示下一层,即 vv.back().push_back(front->val) 为下一层添加二叉树那一层的元素
💻代码实现:
class Solution
{
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> vv;
if (!root)
{
return vv;
}
queue<TreeNode*> q;
q.push(root);
while (!q.empty())
{
int num = q.size();
vv.push_back(vector<int>());
for (int i = 1; i <= num; ++i)
{
TreeNode* front = q.front();
q.pop();
vv.back().push_back(front->val);
if (front->left)
{
q.push(front->left);
}
if (front->right)
{
q.push(front->right);
}
}
}
return vv;
}
};
3.二叉树的层序遍历 Ⅱ
✏️题目描述:

✏️示例:

传送门: 二叉树的层序遍历 Ⅱ
题解:
这题其实和上面的题逻辑实现是一样的,从下至上遍历的话,看成从上至下的遍历的反转即可
💻代码实现:
class Solution
{
public:
vector<vector<int>> levelOrderBottom(TreeNode* root)
{
vector<vector<int>> vv;
if (!root)
{
return vv;
}
queue<TreeNode*> q;
q.push(root);
while (!q.empty())
{
int num = q.size();
vv.push_back(vector<int>());
for (int i = 1; i <= num; ++i)
{
TreeNode* front = q.front();
q.pop();
vv.back().push_back(front->val);
if (front->left)
{
q.push(front->left);
}
if (front->right)
{
q.push(front->right);
}
}
}
reverse(vv.begin(), vv.end());
return vv;
}
};
4.二叉树的最近公共祖先
✏️题目描述:

✏️示例:

传送门: 二叉树的最近公共祖先
题解:
据题目多种情况分析可知一共有三种情况:
🚩p和q都在根节点右支

🚩p和q都在根节点左支
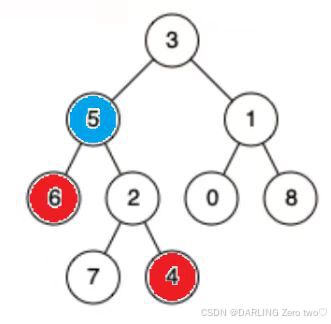
🚩p和q都在根节点左支和右支

排除了p或q为根节点的情况,那么剩余的情况必定在根节点以下的节点,发现用向下递归的方法,都在右支或都在左支的情况最后都能被化成子树根节点的左支和右支问题

💻代码实现:
class Solution
{
public:
bool Find(TreeNode* tree, TreeNode* x)
{
if (tree == nullptr)
{
return false;
}
return tree == x
|| Find(tree->left, x)
|| Find(tree->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if (root == nullptr)
{
return nullptr;
}
if (root == p || root == q)
{
return root;
}
bool pLeft, pRight, qLeft, qRight;
pLeft = Find(root->left, p);
pRight = !pLeft;
qLeft = Find(root->left, q);
qRight = !qLeft;
if (qLeft && pLeft)
{
return lowestCommonAncestor(root->left, p, q);
}
else if(qRight && pRight)
{
return lowestCommonAncestor(root->right, p, q);
}
else
{
return root;
}
}
};
5.二叉搜索树与双向链表
✏️题目描述:
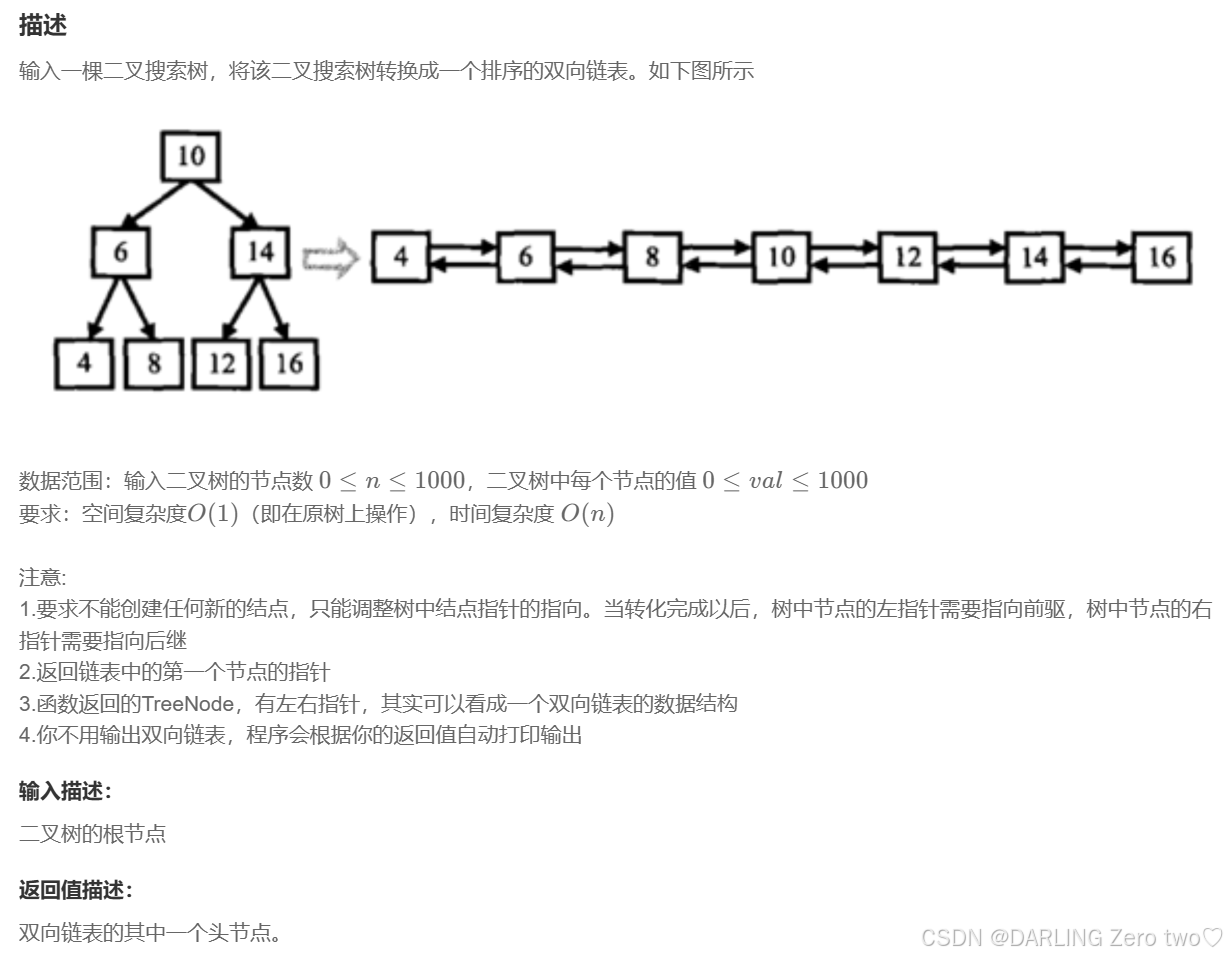
✏️示例:

传送门: 二叉搜索树与双向链表
题解:
看双向链表可知,这是一个典型的中序遍历,左节点、节点、右节点的顺序,那么双向链表的节点顺序解决了,就要考虑节点的链接,前驱节点直接链接上一个中序遍历的节点,后驱节点则是下一个,最后返回最左下角的节点(即 head )
💻细节问题:
注意 prev 每次赋值完之后要更新一次,为下一个节点做准备,同时要以引用形式传递,全程只有一个 prev 在改变,不加引用的话就是不同层级递归下的 prev,这之间的 prev的改变不会互相影响,无法形成正确的链表关系
💻代码实现:
class Solution
{
public:
void Inorder(TreeNode* cur, TreeNode*& prev)
{
if (cur == nullptr)
return;
Inorder(cur->left, prev);
cur->left = prev;
if (prev)
{
prev->right = cur;
}
prev = cur;
Inorder(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* prev = nullptr;
Inorder(pRootOfTree, prev);
TreeNode* head = pRootOfTree;
while (head && head->left)
{
head = head->left;
}
return head;
}
};
6.从前序与中序遍历序列构造二叉树
✏️题目描述:

✏️示例:

传送门: 从前序与中序遍历序列构造二叉树
题解:

首先我们要知道,前序是按照先左根再右根的顺序进行,这也决定了他是二叉树中根的顺序,其次中序的遍历方式我们可以发现找到前序中的根,那么其左右区间就是左右子树,按照此种方法不断划分,就是利用的分治思想
💻细节问题: 当 inbegin > inend 时,也就是最后返回空值的情况别忘了
💻代码实现:
class Solution
{
public:
TreeNode* _build(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
{
if (inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(preorder[prei]);
int rooti = inbegin;
while (rooti <= inend)
{
if (preorder[prei] == inorder[rooti])
break;
++rooti;
}
++prei;
root->left = _build(preorder, inorder, prei, inbegin, rooti-1);
root->right = _build(preorder, inorder, prei, rooti+1, inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int i = 0;
return _build(preorder, inorder, i, 0, inorder.size() - 1);
}
};
7.从中序与后序遍历序列构造二叉树
✏️题目描述:

✏️示例:

传送门: 从中序与后序遍历序列构造二叉树
题解:
这题与上一题的实现逻辑是一样的,中序负责划分左右区域,后序负责找节点,不过是从右子树开始罢了,要从数组 postorder 结尾往前走
💻代码实现:
class Solution
{
public:
TreeNode* _build(vector<int>& inorder, vector<int>& postorder, int& prei, int inbegin, int inend)
{
if (inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(postorder[prei]);
int rooti = inbegin;
while (rooti <= inend)
{
if (postorder[prei] == inorder[rooti])
break;
++rooti;
}
--prei;
root->right = _build(inorder, postorder, prei, rooti+1, inend);
root->left = _build(inorder, postorder, prei, inbegin, rooti-1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
int i = postorder.size() - 1;
return _build(inorder, postorder, i, 0, inorder.size() - 1);
}
};
8.二叉树的前序遍历(非递归)
✏️题目描述:

✏️示例:

传送门: 二叉树的前序遍历(非递归)
题解:
这里直接说明非递归的方法,其实和递归的思想差不多,但这里是用的循环,用非递归是因为递归在某些情况可能造成栈溢出

每次遍历将操作的数入栈,输出的结果放在数组里
- 遍历左路节点
- 遍历左树节点的右路
对上面的步骤进行循环操作即可,直到栈内的数已经 pop 完说明已经结束
💻代码实现:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
TreeNode* cur = nullptr;
if (root)
cur = root;
vector<int> v;
while (cur || !st.empty())
{
while (cur)
{
v.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
return v;
}
};
9.二叉树的中序遍历(非递归)
✏️题目描述:

✏️示例:

传送门: 二叉树的中序遍历(非递归)
题解:
这题和上一题的思路基本一致,只不过是顺序有所改变
- 左路节点入栈
- 访问左路节点及左路节点的右子树
💻代码实现:
class Solution
{
public:
vector<int> inorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
TreeNode* cur = nullptr;
if (root)
cur = root;
vector<int> v;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
cur = top->right;
}
return v;
}
};
10.二叉树的后序遍历(非递归)
✏️题目描述:

✏️示例:

传送门: 二叉树的后序遍历(非递归)
题解:

后序遍历其实也是和上面差不多,但是需要确认右路是否访问过,不然会陷入死循环,所以定义一个 prev 来确认是否访问过
💻代码实现:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
TreeNode* prev = nullptr;
TreeNode* cur = nullptr;
vector<int> v;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
if (top->right == nullptr || top->right == prev)
{
prev = top;
v.push_back(top->val);
st.pop();
}
else
{
cur = top->right;
}
}
return v;
}
};
希望读者们多多三连支持
小编会继续更新
你们的鼓励就是我前进的动力!

























 5738
5738

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








