逻辑回归和线性回归的最终目标都是拟合一个线性函数 y=θTx y = θ T x ,使得我们的预测输出和真实输出之间的差异最小。它们的区别在于损失函数不一样,线性回归的损失函数( MSE M S E )是基于模型误差服从正态分布的假设推导出来的,而逻辑回归的损失函数则是基于极大似然的假设推导出来的,即所有样本结果的后验概率乘积最大。
预测函数
因为我们利用超平面
θTx=0
θ
T
x
=
0
来分类,所以当一个样本落在超平面上,我们就可以认为该样本为正样本的概率等于负样本的概率,即:
对上式两边取对数:
因为 P(y=1|x)+P(y=−1|x)=1 P ( y = 1 | x ) + P ( y = − 1 | x ) = 1 ,所以可以得到:
整理可得:
所以 P(y=−1|x)=1−P(y=1|x)=11+eθTx P ( y = − 1 | x ) = 1 − P ( y = 1 | x ) = 1 1 + e θ T x , P(y=1|x) P ( y = 1 | x ) 的分子分母同时除以 eθTx e θ T x 得到 11+e−θTx 1 1 + e − θ T x ,这就是 sigmoid s i g m o i d 函数的推导过程。其函数曲线如下图所示:
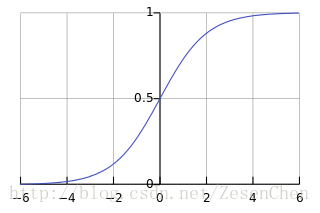
我们可以将其理解为一种非线性变换,目的是把 (−∞,+∞) ( − ∞ , + ∞ ) 的数值映射到0到1之间,我们将映射结果视为 y=1 y = 1 概率。 sigmoid s i g m o i d 函数有一个重要的性质:
该性质在后面求偏导数的时候会用到。
目标函数
我们令
h(x)=11+e−θTx
h
(
x
)
=
1
1
+
e
−
θ
T
x
,由前面的推导可以将
h(x)
h
(
x
)
理解为样本点
x
x
为正样本的概率,即
P(y=1|x)=h(x)
P
(
y
=
1
|
x
)
=
h
(
x
)
。根据极大似然估计的思想,各个样本的结果出现总概率(即后验概率乘积)需要达到最大值,即:
因为 1−h(x)=h(x) 1 − h ( x ) = h ( x ) ,所以上式取对数后可以得到:
这便是逻辑回归的优化目标函数,它的最终形式表示为:
在吴恩达的机器学习课程中,逻辑回归的目标函数形式为:
是因为它将负样本 yi y i 表示为0,它和我们推导出来的结果本质是相同的。
梯度下降
我们推导过程中有一步为:
max{∑Ni=1ln(h(yixi))}
m
a
x
{
∑
i
=
1
N
l
n
(
h
(
y
i
x
i
)
)
}
,为了方便利用
sigmoid函数的求导性质
s
i
g
m
o
i
d
函
数
的
求
导
性
质
,我们便把这个式子作为优化目标。要求一个凸函数的最大值,更新公式为:
令 g(θTx)=h(x)=11+e−θTx g ( θ T x ) = h ( x ) = 1 1 + e − θ T x ,优化目标可以变换为: J(θ)=max{∑Ni=1ln(g(yiθTxi))} J ( θ ) = m a x { ∑ i = 1 N l n ( g ( y i θ T x i ) ) } ,对我们的优化目标进行求导:
所以梯度下降的更新方程为:
代码块
自己用python撸了个逻辑回归,有问题请留言评论区:
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import scale
from random import random
from numpy import random as nr
from sklearn.model_selection import train_test_split
def sigmoid(x):
return 1/(1+np.exp(-x))
def RandSam(train_data, train_target, sample_num):#随机采样传入训练函数进行迭代
data_num = train_data.shape[0]
if sample_num > data_num:
return -1
else:
data = []
target = []
for i in range(sample_num):
tmp = nr.randint(0,data_num)
data.append(train_data[tmp])
target.append(train_target[tmp])
return np.array(data),np.array(target)
class LogisticClassifier(object):
alpha = 0.01
circle = 1000
l2 = 0.01
weight = np.array([])
def __init__(self, learning_rate, circle_num, L2):
self.alpha = learning_rate
self.circle = circle_num
self.l2 = L2
def fit(self, train_data, train_target):
data_num = train_data.shape[0]
feature_size = train_data.shape[1]
ones = np.ones((data_num,1))
train_data = np.hstack((train_data,ones))
#Y = train_target
self.weight = np.round(np.random.normal(0,1,feature_size+1),2)
for i in range(self.circle):
delta = np.zeros((feature_size+1,))
X,Y = RandSam(train_data, train_target, 50)
for j in range(50):
delta += (1-sigmoid(Y[j]*np.dot(X[j],self.weight)))* \
Y[j]*X[j]
self.weight += self.alpha*delta-self.l2*self.weight
def predict(self, test_data):
data_num = test_data.shape[0]
ones = np.ones((data_num,1))
X = np.hstack((test_data,ones))
return sigmoid(np.dot(X,self.weight))
def evaluate(self, predict_target, test_target):
predict_target[predict_target>=0.5] = 1
predict_target[predict_target<0.5] = -1
return sum(predict_target==test_target)/len(predict_target)
if __name__ == "__main__":
cancer = load_breast_cancer()
xtr, xval, ytr, yval = train_test_split(cancer.data, cancer.target, \
test_size=0.2, random_state=7)
logistics = LogisticClassifier(0.01,2000, 0.01)
logistics.fit(xtr, ytr)
predict = logistics.predict(xval)
print('the accuracy is ',logistics.evaluate(predict, yval),'.')




 本文详细阐述了逻辑回归的基本原理,包括预测函数的推导、目标函数的形式以及梯度下降法的应用,并通过Python代码实现了逻辑回归模型。
本文详细阐述了逻辑回归的基本原理,包括预测函数的推导、目标函数的形式以及梯度下降法的应用,并通过Python代码实现了逻辑回归模型。
















 5740
5740

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








