电路分析 第七章（相量法基础）

一、复数

1、复数的表现形式

（1）代数形式：（在电路中通常用j来代替i，a为实部，b为虚部）

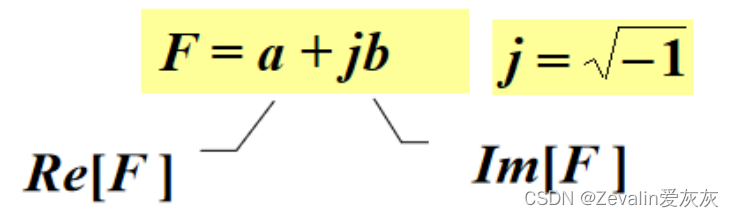
（2）三角函数形式：

（3）在复平面上表示：

（4）指数形式：

（5）极坐标形式：（|F|为矢径，∠φ为极角）

        极坐标与直角坐标的关系：

2、复数的四则运算

（1）加减运算：

（2）乘法运算：

（3）除法运算：

3、旋转因子

（1）对于复数，相当于把逆时针旋转一个角度，而模不变。故把称为旋转因子。

（2）几种不同值时的旋转因子：

二、正弦电压和电流

1、正弦量

（1）交流电原理：当线圈在磁场中旋转时，对应不同位置，线圈切割磁力线数不同，所产生的感应电压按正弦规律产生变化，线圈旋转一周，对应的角度变化为2π。

（2）随时间按正弦规律变化的电流或电压等变量称为正弦量。

（3）瞬时值表达式：

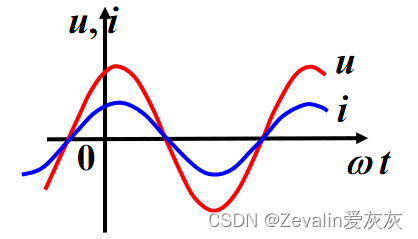
（4）波形图：

（5）正弦量为周期函数，可表示为，其中K为正整数，T为周期。

①重复变化一次所需的时间称为周期，单位为s（秒）。

②每秒重复变化的次数称为频率，单位为Hz（赫兹）。

③频率和周期互为倒数。

（6）正弦交流电路：激励和响应均为正弦量的电路（正弦稳态电路）称为正弦交流电路，简称正弦电路或交流电路。

（7）研究正弦电路的意义：

①正弦稳态电路在电力系统和电子技术领域占有十分重要的地位，它容易产生、传送和使用。

②正弦信号是一种基本信号，任何变化规律复杂的信号几乎都可以分解为按正弦规律变化的分量。

2、正弦量的三要素

（1）表示正弦量随时间变化的进程，称之为相位角，它的大小决定该时刻正弦量的值。

（2）当t=0时，相位角，故称φ为初相位角，简称初相位，它表示了正弦量的起点。

（3）同一个正弦量，如果计时起点不同，初相位就不同。

3、同频率正弦量的相位差

（1）设，，则二者的相位差为

（2）相位差等于初相位之差。

（3）规定相位差的绝对值不能大于180°，由于正弦函数是一个周期函数，相位差的计算结果是能够控制在该范围内的（对超出范围的计算结果进行±360°即可）。

（4）相位差的正负描述：

①φ>0，u超前iφ角，或i滞后uφ角，说明u比i先到达最大值。

②φ<0，u滞后iφ角，或i超前uφ角，说明i比u先到达最大值。

（5）特殊相位关系：

①相位差φ=0，此时u和i二者同相位（简称同相）。

②相位差φ=π/2，说明u领先iπ/2，i落后uπ/2。

③相位差φ=±π，两个正弦量相位差了半个周期，这种情况称u和i反相。

4、周期性电流、电压的有效值

（1）周期性电流、电压的瞬时值随时间而变，为了衡量其平均效果，工程上采用有效值来表示。

（2）有效值也称为均方根值，交流电通过电阻后会产出相应的能量，取交流电的一个周期，在该时间段内如果给该电阻通以一个恒定电流，也能够产出相同的能量，恒定电流的大小就是交流电的电流有效值。

（3）正弦电流、电压的有效值：

（4）工程上说的正弦电压、电流一般指有效值，如设备铭牌额定值、电网的电压等级等，但绝缘水平、耐压值指的是最大值。因此，在考虑电器设备的耐压水平时应按最大值考虑。

三、正弦量的相量表示

1、相量法概述

（1）用相量表示各正弦量，从而分析或寻求各量之间关系的方法就是相量法。

（2）相量法只适用于激励为同频正弦量的非时变线性电路，也就是只用来分析正弦稳态电路。

2、正弦量的具体相量表示

（1）以正弦电流为例，设，根据欧拉公式有

        上式中，Re[]是取复数实部的运算。上式将正弦量与复指数函数联系起来，可见用余弦函数表示的正弦量可表示为一复指数函数的实部，该复指数函数的复常数因子包含了正弦量的两个要素——振幅和初相位。在正弦电流电路中，各电流及电压的频率与电源的频率相同，这是已知的，因此正弦电流电路的电流和电压由其振幅和初相位唯一确定，即由其对应的复变函数的负常数因子确定。

（2）将上式中的复常数因子定义为正弦电流的振幅相量，记为

        定义正弦电流的有效值相量为

①振幅相量和有效值相量都简称为相量，它们同样满足根号二的关系，根据相量符号是否有下表m可对二者进行区分。同理可定义正弦电压及其它正弦量的相量。

②相量的模表示正弦量的有效值，相量的辐角表示正弦量的初相位。

（3）相量是复数，其运算与一般复数运算相同。每一个相量都对应着一个正弦量，这是其与一般复数的不同之处，因此在相量的符号上加一个小圆点以示区别。

（4）相量也可用复平面的相量图表示，称为正弦量的相量图，利用相量图可直观地看出各正弦量之间的相位关系。不同频率的相量不能画在同一张相量图上，也就是说不同频率的相量之间不能进行运算。

（5）正弦量与它的相量是一一对应的，由正弦量时间表达式可直接写出它的相量，或由相量直接写出与之对应的正弦量的时间函数。

（6）关于相量法的几点说明：

①所谓相量法是用相量这一特殊的复数形式来保释正弦量，从而将正弦量的运算转化为相量（复数）运算的方法，引入相量的目的是为了简化正弦稳态电路的分析计算。

②将正弦量用相量表示实质上是一种数学变换，务必记住正相量和相量只是一种对应关系，两者并不等同。

3、相量法的应用

（1）同频正弦量相加减运算可变成对应相量的相加减运算。（下图所示的是加法运算，减法同理）

（2）正弦量的微分，积分：

四、电路定律的相量形式

1、基尔霍夫定律的相量形式

流入某一节点的所有正弦电流用相量表示时仍满足KCL，任一回路所有支路正弦电压用相量表示时仍满足KVL。

2、电阻元件VCR的相量形式

（1）波形图和相量图：

（2）瞬时功率：瞬时功率以2为周期交变，始终大于零，表明电阻始终吸收功率。

3、电感元件VCR的相量形式

（1）感抗和感纳：

①称为感抗，单位为Ω（欧姆）。

②称为感纳，单位为S（西门子）。

（2）感抗表示限制电流的能力，感抗和频率成正比。

（3）波形图和相量图：

（4）瞬时功率：瞬时功率以2为周期交变，有正有负，一周期内刚好互相抵消。

4、电容元件VCR的相量形式

（1）容抗与容纳：

①称为容抗，单位为Ω（欧姆）。

②称为容纳，单位为S（西门子）。

（2）容抗和频率成反比。

（3）波形图和相量图：

（4）瞬时功率：瞬时功率以2为周期交变，有正有负，一周期内刚好互相抵消。

5、单一参数电路中复数形式的欧姆定律

（1）复数形式的欧姆定律和直流电路中的形式相似。

（2）正弦稳态电路中R、L、C元件电压、电流之间关系的相量形式完全与电阻的欧姆定律相似，因此称它们为相量形式的欧姆定律。