动态规划及例题

一、动态规划

       动态规划算法通常用于解决最优化问题（寻求最优解）。其思想与分治法类似，将待求解的问题分成若干个子问题，先求出子问题，再根据子问题的解求出原来问题中的解，与分支法不同的是，在动态规划中，这些子问题的解是不相互独立的。

        采用动态规划求解的问题通常有以下性质：

        1.最优化原理：问题的最优解中包含的子问题的解也是最优的。

        2.无后效性：即某阶段状态一旦确定，就不受该状态以后决策的影响，只与当前状态有关。

        3.有重叠子问题：子问题之间是不相互独立的，一个子问题在下一阶段的决策中可能被多次用到。（通常减少不必要的重复操作）

二、钢条切割问题        

        给定一段长度为 n 的钢条和一个价格表 pi ，求钢条切割方案使得销售收益 rn 最大。

长度I	1	2	3	4	5	6	7	8	9	10
价格pi	1	5	8	9	10	17	17	20	24	30

        案例：长度为 4 的钢条，如何切割使得销售额最高？

        考虑两种情况：1.切割成4个长度为1的钢条，总收益是4；

                                  2.切割成2个长度为2的钢条，总收益是10。

                                  3.切割成1个长度为1和一个长度为3的钢条，总收益是9

                                 4.切割成1个长度为4的钢条，总收益为9

        法一（易理解）

        对于求收益r[n]最大的切割方案（最优解）

        1.不切割，收益为 pn

        2.先将该钢条分为切为两根，则当该两根钢条的收益之和最大时（取最优解时），对应长度为n的钢条收益也最大，最优解的和就是当前情况的最优解，可以得出：

                 

        法二 （简单）

        对于该求解方法可以改为一种相似但更简单的递归求解方法：

        将钢条从左边切割下长度为 i 的一段，只对右边剩下的长度为 n-i 的一段继续进行切割（递归求解），对左边的一段不再进行切割。

关于此想法的理解：

将长度为n的钢条分解为左边开始一段，以及剩余部分继续分解的结果（通过递归） 

或者理解为：对于一根长度为n钢条，总存在某种切割，会使得切出长度为 i 的钢条 

           此时公式为：

                                

           递归函数的伪代码为：

int get_best(int n)
{
	if(n<=0) return 0;
	int maxn=-1;
	for(int i=1;i<=n;i++)
		maxn=max(p[i]+get_best(n-i),maxn);  // 通过递归求出最大
	//r[n]=maxn;
	return maxn;
}

        根据代码不难发现，在递归函数get_best中，会存在同一个变量反复递归的情况，从而引起时间的浪费，此时时间复杂度达到 O(2^n)

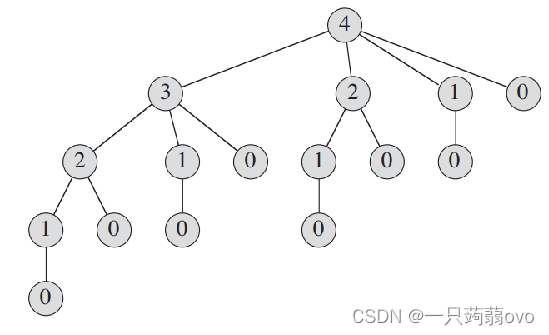
        需要通过剪枝的方法避免重复的操作（自顶向下法）

int get_best(int n)
{
	if(n<=0) return 0;
	if(r[n]>0) return r[n]; // 若已经访问过，即找到r[n]的最优解时，直接返回
	int maxn=-1;
	for(int i=1;i<=n;i++)
		maxn=max(p[i]+get_best(n-i),maxn);
	r[n]=maxn;
	return maxn;
}

  此外，还可以通过自底向上的方法求出最优解，此时为递推操作，不需要递归

int get_best2(int n)
{
	for(int i=1;i<=n;i++)
	{
		r[i]=p[i]; // 直接将 长度为 i的切割下 
		for(int j=1;j<i;j++)
			r[i]=max(r[i],p[j]+r[i-j]); //免去递归操作 
	}
 } 

         重构解

        将最优解的切割方案求出

int get_best2(int n)
{
	for(int i=1;i<=n;i++)
	{
		r[i]=p[i]; // 直接将 长度为 i的切割下 
		s[i]=i;
		for(int j=1;j<i;j++)
		if(r[i]<p[j]+r[i-j])  //免去递归操作 
		{
			r[i]=p[j]+r[i-j];
			s[i]=j;  // 表示当长度为i时，将切割长度为j的钢条 ,剩余 i-j 已经求出最优解和切割方案了 
		}
	}
	int x=n;
	while(x>0)
	{
		printf("%d ",s[x]);
		x-=s[x];
	}
}

此过程只需在求解规模为 i 的子问题时将，第一段钢条的最优切割长度j保存在 s [ i ] 中

三、矩阵链问题

        问题描述
        给定n个矩阵的链(A1,A2,…,An)，矩阵A的规模为pi-1 x pi (1<=i<=n)，求完全括号化方案，使得计算乘积A1A2….An所需标量乘法次数最少。
        注意：求解矩阵链乘法问题并不是要真正进行矩阵相乘运算，我们的目标只是确定代价最低的计算顺序。确定最优计算顺序所花费的时间通常要比随后真正进行矩阵相乘所节省的时间要少。

关于矩阵乘法次数的具体例子比较：

        第一种乘法顺序   5*3*100+5*100*5=4000

        第二种乘法顺序   3*100*5+5*3*5=1575

        分析过程：

        计算最优解，不妨可以先找出最优解的子问题，即假设 AiAi+1---Aj的最优括号化分割点在Ak-Ak+1之间，那么则其前链 Ai-Ak 为子链的最佳方案 Ak+1-Aj 也一定为该子链的最佳方案，否则还存在更优的方案。

        括号的划分是从小（子链）到大（长链）的，即可以认为在上述的想法中，两子链中只含有一个分割点，（子链中间也可能含有分割点），则考虑某条长链时，只需要考虑一个分割点即可。从而动态规划中需要考虑链的长度，起始点，终止点，以及分割点。

        动态规划公式：

其中 m[i,j]　表示从从Ai到Aj的最优方案，分割点ｉ～ｊ之间均计算结果取最优。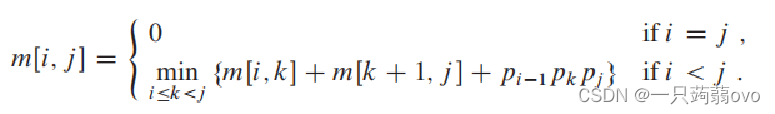

 对于两个矩阵的乘法计算次数：

        A1(d*e)*A2(e*f)   次数为： d*e*f 

则对于上述子链中的计算次数为   Ai---Aj   分割点为Ak  的计算次数为   pi-1*pk*pj 

        代码思想：

        由于上述思想是通过链的长度推导，则需要一个循环记录长度 l ，再记录一个起始点 i，可以通过起始点和长度计算出末尾点 i+l-1，最后再记录一个分割点k，将分割点的每种情况都考虑，得出当前最优方案。

void getbest()
{
    for(int i=1;i<=n;i++)  m[i][i]=0;
    for(int l=2;l<=n;l++)
    {
        for(int i=1;i<=n-l+1;i++)
        {
            int j=i+l-1;
            m[i][j]=10000;// 初始化大一点方便比较
            for(int k=i;k<=j-1;k++)
            {
                q=m[i][k]+m[k][j]+p[i-1]*p[k]*p[j];
                if(q<m[i][j])
                {
                    m[i][j]=q;
                    s[i][j]=k; // 记录路径
                }
            }   
        }
    }
}

         构造最优解：

          找出计算次数的最优方案，即需要找出每个的分割点，在计算最优m[i][j]时，只需要记录出当前在 [i,j] 情况下的分割点。

        通过递归的方法将方案统计出

void print(int x,int y)
{
    if(x==y)
    {
        printf("A%d",x);
        return ;
    }
    else
    {
        printf("(");
        print(x,s[x][y]);
        print(s[x][y]+1,y);
        printf(")");
    }
    return ;
}