“k车问题”&动态规划

最近开始做算法题，准备坚持至少一年。解决完问题可能会来记录一下。
嗯，正式开始之前顺便说说今天的上课的一个细节，权当日记：
上计算机网络的时候，我和旁边的同学讨论我原创的一个算法题。
前面的同学：“你们俩能不能别吵了？”
面对这个学巨，我内心非常惭愧。
然后…
他趴在桌上睡着了…睡着了….

好的，废话说完，进入正题，讲讲我吵到前面这位同学睡觉时讨论的那道题。
这个问题是我再思考八皇后的问题时想到的，实际上，我误以为皇后不能斜着走，跟中国象棋中的车一样，结果就成了八皇后问题的弱化版。

在中国象棋棋盘上有10行9列兵线，现在考虑在棋盘上放k<9个车，使他们互相之间不能吃掉对方，问有多少种方法？如果把棋盘改成m×n的呢？

下面是思路：
设$f(k,n,m)$为k个车放到n×m棋盘上的方案数（k<=min{m,n})
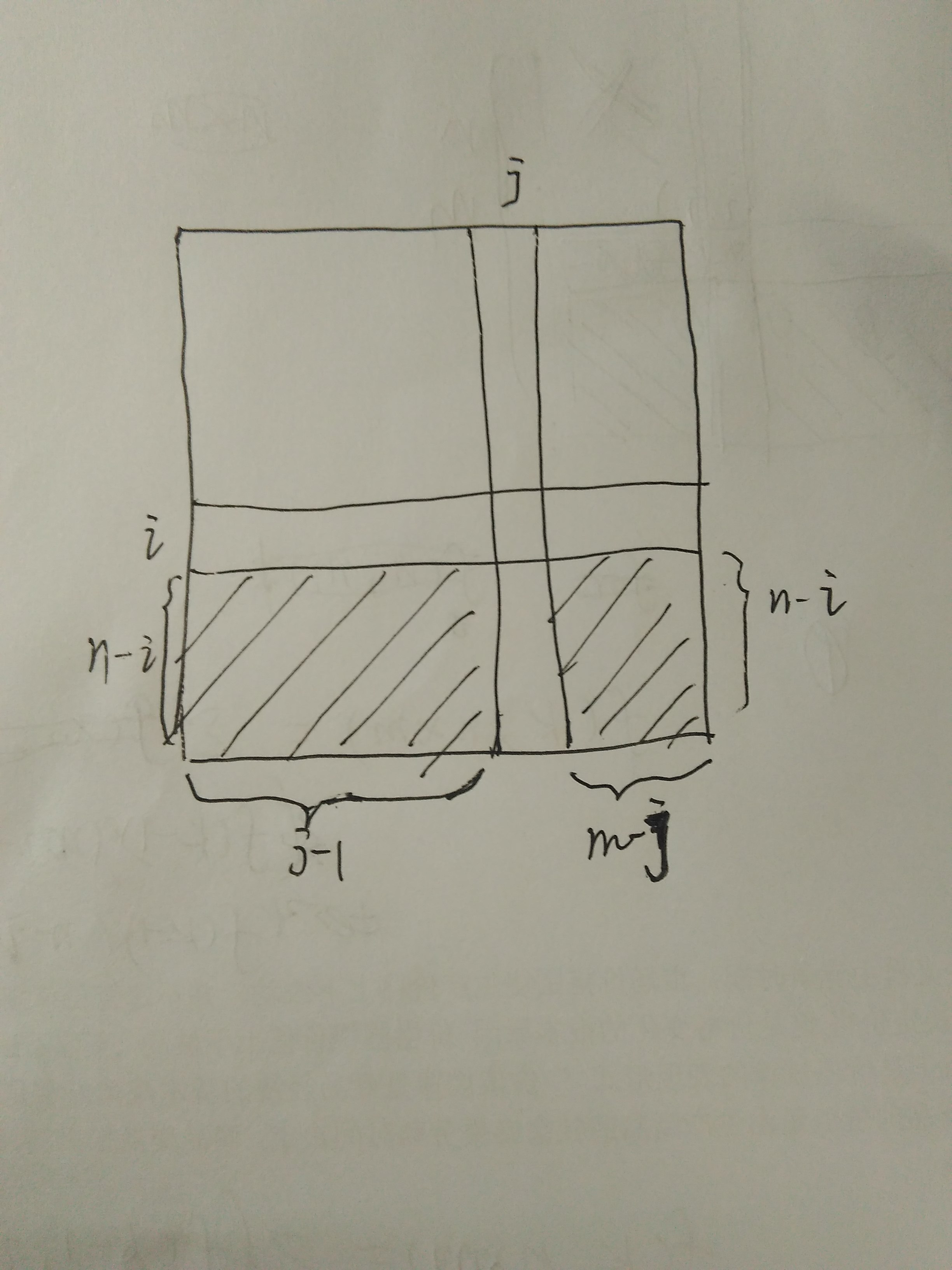
为了避免重复计算，按行为主序排序这m×n个位置。假设选中第一个放车的位置为$(i,j)$，那么前i行和第j列不能再放其他车：第i行和第j列显然不能再放，至于前i-1列为什么不能再放，是因为如果放了，它就排在$(i,j)$前面，$(i,j)$就不是第一个选中的位置了。接下来能放车的位置如下图阴影区域所示。

剩下k-1个点先从左侧阴影区选p（$0\le p\le k-1$)个，有f(p,n-i,j-1)种方案。剩下k-1-p个点从右侧阴影区选择，有f(k-1-p,n-i- p</