PCA降维算法
PCA(Principal Component Analysis)是常见的降维算法之一,它能够将高维度的数据降低到低维度,并且尽可能保持数据丢失率较低。
数学前置知识
PS:本文中所有向量默认是列向量。
直线方程
二维平面中直线方程
在二维平面中确定一个直线需要两个点。设直线的斜率为w,偏置为b,则直线的直角方程可表示为:
y = w x + b y = wx + b y=wx+b
设直线l上有已知固定点Q(x0, y0),倾斜角为θ。直线上一个运动的点P(x, y),设它与Q之间的距离为参数t。则该直线的参数式可写作:
x = x 0 + t ⋅ c o s θ y = y 0 + t ⋅ s i n θ x = x_0 + t \cdot cos \theta \\ y = y_0 + t \cdot sin \theta x=x0+t⋅cosθy=y0+t⋅sinθ
设Q点对应向量为s,P点对应向量为s’,直线的方向向量为u。用向量的表达方式为:
( x y ) = ( x 0 y 0 ) + t ( c o s θ s i n θ ) s ′ = s + t ⋅ u \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} +t \begin{pmatrix} cos \theta \\ sin \theta \end{pmatrix} \\ \ \\ s' = s + t \cdot u (xy)=(x0y0)+t(cosθsinθ) s′=s+t⋅u
三维空间中直线方程
在一个三维空间中确定一个直线除了两点定线的方法外,也可以根据一个定点和对应方向向量确定。设Q(x0, y0, z0),直线的方向向量为s = (a, b, c)T,由直线上任意两点组成的向量与方向向量线性相关。则直线的方程为:
x − x 0 a = y − y 0 b = z − z 0 c \frac {x - x_0} {a} = \frac {y - y_0} {b} = \frac {z - z_0} {c} ax−x0=by−y0=cz−z0
若令上述等式值为t(参数),则可以得到直线参数方程:
x = x 0 + a t y = y 0 + b t z = z 0 + c t x = x_0 + at \\ y = y_0 + bt \\ z = z_0 + ct x=x0+aty=y0+btz=z0+ct
向量的表达形式与二维类似,设直线上已知点对应向量为v,方向向量为s而另外一个线性相关的向量为v’,参数t(表示两点的距离);设该向量与z轴正半轴夹角为φ,在xOy平面投影与x轴正半轴夹角为θ。
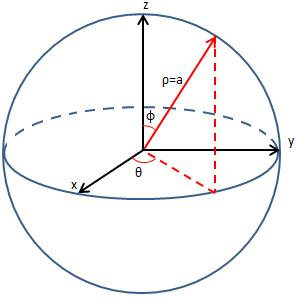
s = ( s i n φ c o s θ ; s i n φ s i n θ ; c o s φ ) v ′ = v + t ⋅ s s = (sin \varphi cos \theta; sin \varphi sin \theta; cos \varphi) \\ v' = v + t \cdot s s=(sinφcosθ;sinφsinθ;cosφ)v′=v+t⋅s
类比可以得到,n维空间中的任意一个向量x’可用另外一个与其线性相关的向量x和它们之间的距离t以及对应单位方向向量s表示,即
x ′ = x + t ⋅ s x' = x + t \cdot s x′=x+t⋅s
向量的内积
向量的内积在二维空间上具有强力的几何特征,根据如下数学公式,向量内积等于两个向量的模的乘积再乘以两个向量的夹角。
α ⋅ β = ∣ α ∣ ⋅ ∣ β ∣ c o s < α , β > α \cdot β = |\alpha| \cdot |\beta| cos<α,β> α⋅β=∣α∣⋅∣β∣cos<α,β>
如果β是单位向量,则上述内积变几何上表示为向量α在向量β方向上的投影。
因此一个向量与单位向量的内积可看做向单位向量所在有向线段上的投影(二维降为一维)。
矩阵的特征分解
若一个n阶矩阵A存在一个可逆的矩阵P使得下式成立:
Λ = P − 1 A P \Lambda = P^{-1}AP Λ=P−1AP
矩阵A相似于对角矩阵Λ,则称矩阵A可特征分解。
性质:若n阶矩阵A有n个线性无关的特征向量或者n阶矩阵A所有特征值对应代数重数等于几何重数,则A相似于对角矩阵(可特征分解)。另外,实对称矩阵必可相似对角化。(PS: 矩阵的代数重数的值等于重根个数,几何重数是对应特征值对应线性方程组基础解系向量个数)
( λ − 1 ) 2 ( λ − 2 ) = 0 , 则 A 特 征 值 λ = 1 的 代 数 重 数 是 2 ( E − A ) X = 0 基 础 解 系 向 量 的 个 数 等 于 n − r ( E − A ) , 也 是 λ = 1 对 应 几 何 重 数 值 (\lambda - 1)^2(\lambda - 2) = 0 \quad , 则A特征值\lambda = 1的代数重数是2 \\ (E - A)X = 0 \ 基础解系向量的个数等于n - r(E - A),也是\lambda = 1对应几何重数值 (λ−1)2(λ−2)=0,则A特征值λ=1的代数重数是2(E−A)X=0 基础解系向量的个数等于n−r(E−A),也是λ=1对应几何重数值
矩阵的特征分解的流程:
- 求矩阵A的特征多项式方程并初步解得A的特征值λ与对应代数重数p。
- 求解齐次线性方程组(λE - A)X = 0的基础解系及其几何重数q
- 若所有p = q则n阶矩阵A可相似与对角矩阵,反之无法直接特征分解。
- 将上述方程组的基础解系对应向量组成矩阵P,特征值按照向量摆放顺序构成对角矩阵Λ。
矩阵的奇异值分解SVD
矩阵的特征分解首先需要矩阵是方阵,n阶矩阵拥有n个线性无关的特征向量或者对应特征值的代数重数等于几何重数,这是相当强烈的条件。如果一个矩阵无法满足,则无法进行特征分解。矩阵的SVD分解将m*n矩阵A分解为三个矩阵的乘积形式,SVD分解对于任何实矩阵都成立:
A m ∗ n = U m ∗ m Σ m ∗ n V n ∗ n T A_{m*n} = U_{m*m} \Sigma _{m*n} V_{n*n}^T Am∗n=Um∗mΣm∗nVn∗nT
其中矩阵U,V为正交矩阵,分别又被称作左、右奇艺向量。Σ 是一个类对角矩阵(不一定是方阵),除了主对角线元素外其余元素均为0。尽管矩阵A无法进行特征分解,但是它的转制矩阵AT与它的乘积ATA是一个对称矩阵一定能进行特征分解。
A T A = V Σ T U T U Σ V T = V T Σ 2 V A A T = U Σ V T V Σ T U T = U Σ 2 U T A^TA = V \Sigma ^T U^T U \Sigma V^T = V^T \Sigma ^2V \\ AA^T = U \Sigma V^T V \Sigma ^T U^T = U \Sigma ^2 U^T ATA=VΣTUTUΣVT=VTΣ2VAAT=UΣVTVΣTUT=








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3179
3179











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








