本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念,使读者快速入门,故不追求难度和深度,仅起到抛砖引玉的作用。 
在XCPC中有一种题叫计算几何,这类题在大多数时候都作为一类金牌题甚至防AK题的难度出现,但是在前段时间我写了许多学习计算几何的博客,会发现计算几何的知识体系十分独立且庞大,而且板子很长,就是一个特点:毒瘤。
所以,在这里,我作为一个主修计算几何的ACMer,做了一点点题后对这类毒瘤题做出了一定的总结,希望对大家能有所帮助。 首先,计算几何的题目并非全是难题,它也有一个难度梯度,我这边将其分为差不多三类题:
1.一般的平面几何知识的运用,一般这类题难度较低,需要掌握基本的几何知识和计算几何代码能力即可,一般这类题一般作为XCPC的铜牌难度及以下,在大多数省赛中作为一个区分水平的题目。
2.与一些ACM的惯用算法及数据结构以及一些几何算法考在一起的较难题,这类题一般作为XCPC中的银牌题至金牌题中出现,具有较高的区分度。
3.一类考的比较多的经典题型:寻找某一个参数,可能是一个点,一条直线,用于 满足一个特定函数的极值或者求某些参数的几何期望。这类题的难度一般放在XCPC中的防ak机制中,做法较为明确但是由于代码的复杂程度与精度的设置导致一般通过率很低。
在这里告诉大家笔者的计算几何水平十分一般,少有能在赛时写出来这种,但是还是有一些不错的经验,赛时赛后也是苦苦钻研的这类题,有些不错的题目给大家讲解下😄:
第一类 : 基本的平面&空间几何知识运用题
T1:简单几何计算

题目来源:
Attachments - 2018 German Collegiate Programming Contest (GCPC 18) - Codeforces
题解:
本题出自2018年GCPC,题意是给你一个起点和一个终点,保证在一个蓝色的圆形区域内,再给你一个红色圆形区域,要求你找到一条最短的路径从起点走到终点且不经过红色的圆。那么做计算几何题我们先将这题的模型建立出来: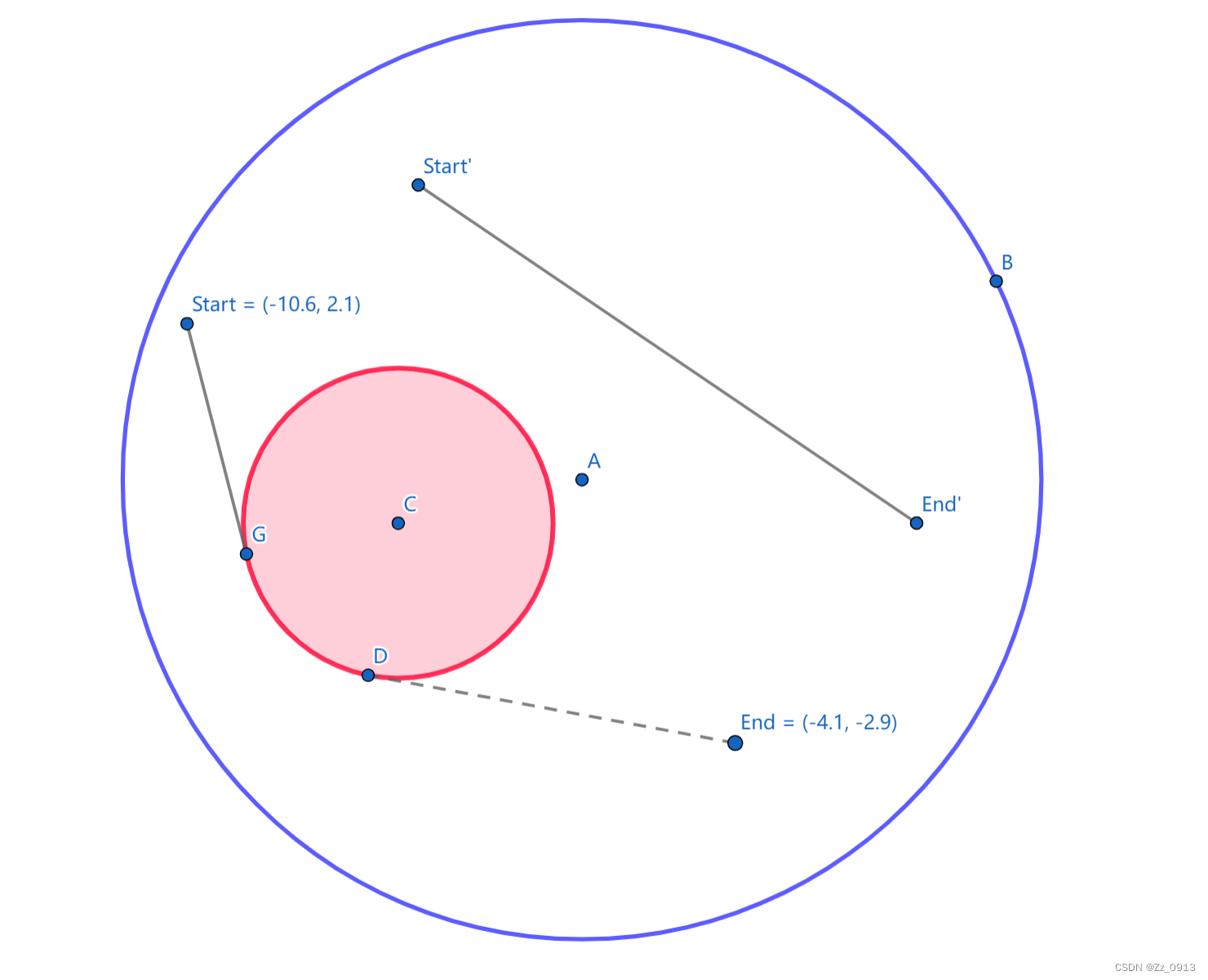
那么答案就显而易见了,最简单的计算几何题,我们进行分类讨论:
1.两点所构成的线段穿过圆,那么路径为两个切点到两点的线段长度加上两个切点所构成的圆弧长度。
2.两点所构成的线段与圆相切或相离,那答案就是两点的欧拉距离。
接下来给出我的代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 10;
const double Eps = 1e-10;
const double pi = acos(-1.0);
const int QAQ = 0;
double xc,yc,xd,yd,xb,yb,rb,xr,yr,rr;
int Dcmp(double x)
{
if(fabs(x) < Eps) return 0;
return x < 0 ? -1 : 1;
}
double Norm(double x)
{
return min(max(x, -1.0), 1.0);
}
double sqr(double x) { return x * x;}
struct Point{
double x,y;
Point(double x = 0,double y = 0) : x(x) , y(y) {};
}point[MAXN];
typedef Point Vector;
Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}
Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}
Vector operator * (Vector Alpha,double x) { return Vector(Alpha.x * x,Alpha.y * x);}
Vector operator / (Vector Alpha,double x) { return Vector(Alpha.x / x,Alpha.y / x);}
double Dis(Point Alpha,Point Beta)
{
return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));
}
double Cross(Vector Alpha,Vector Beta) { return Alpha.x * Beta.y - Alpha.y * Beta.x;}
double Area(Point Alpha,Point Beta,Point Gama)
{
return (Cross(Beta - Alpha,Gama - Alpha) / 2);
}
int main()
{
int _;
_ = 1;
while (_--)
{
cin>>xc>>yc;
cin>>xd>>yd;
cin>>xb>>yb>>rb;
cin>>xr>>yr>>rr;
Point X = Point(xc,yc),Y = Point(xd,yd),Z = Point(xr,yr);
double A = sqr(Y.x - X.x) + sqr(Y.y - X.y);
double B = 2.0 * (Y.x - X.x) * (X.x - Z.x) + 2.0 * (Y.y - X.y) * (X.y - Z.y);
double C = sqr(X.x - Z.x) + sqr(X.y - Z.y) - sqr(rr);
double Delta = B * B - 4.0 * A * C;
if(Dcmp(Delta) < 0) cout<<fixed<<setprecision(10)<<sqrt(sqr(xc - xd) + sqr(yc - yd))<<'\n';
if(Dcmp(Delta) >= 0)
{
double t1 = (-B - sqrt(Delta)) / (2.0 * A);
double t2 = (-B + sqrt(Delta)) / (2.0 * A);
if(Dcmp(t2) < 0 || Dcmp(t1 - 1.0) > 0)
cout<<fixed<<setprecision(10)<<sqrt(sqr(xc - xd) + sqr(yc - yd))<<'\n';
else
{
double OC = Dis(Z,X),OD = Dis(Z,Y),CD = Dis(X,Y);
double OA = rr,OB = rr;
double AC = sqrt(sqr(OC) - sqr(OA));
double BD = sqrt(sqr(OD) - sqr(OB));
double AOC = acos(OA / OC);
double BOD = acos(OB / OD);
double COD = acos(Norm((sqr(OC) + sqr(OD) - sqr(CD)) / (2.0 * OC * OD)));
if(Dcmp(COD) == 0) COD = pi;
double AOB = COD - BOD - AOC;
cout<<fixed<<setprecision(10)<<AC + BD + AOB * rr<<'\n';
}
}
}
return QAQ;
}
T2:应用问题的建模
题目来源:Attachments - 2023 CCPC Henan Provincial Collegiate Programming Contest - Codeforces
题解:
本题出自2023年的河南省赛,赛时过的队数并不多,但是笔者还算研究过一点计算几何,所以这题还是轻松解出了,题目大意是:我们有一个线段AB,还有一个可以运动的质点,已知运动时间为t,运动速度为v,那么运动范围是以起点为圆心,运动区域为vt为半径的一个圆形区域。以速度v移动时间t,最后距离起点最远距离为v×t。显然 以起点为圆心,v×t为半径的圆内都是危险区域。 考虑危险区域的其他边界,即考虑点Q在圆周上移动时三 角形QAB的变化情况,显然危险区域的边界除部分圆周外,还 包括和圆相切时的线段QA和QB。因此分三种情况对危险区域 计算面积即可:那么QAB只需要考虑AB与圆之间的位置关系,即线段AB与圆相离,线段AB与圆相切,线段AB与圆相交,那么建模出来的情况具体分为如下三种✌: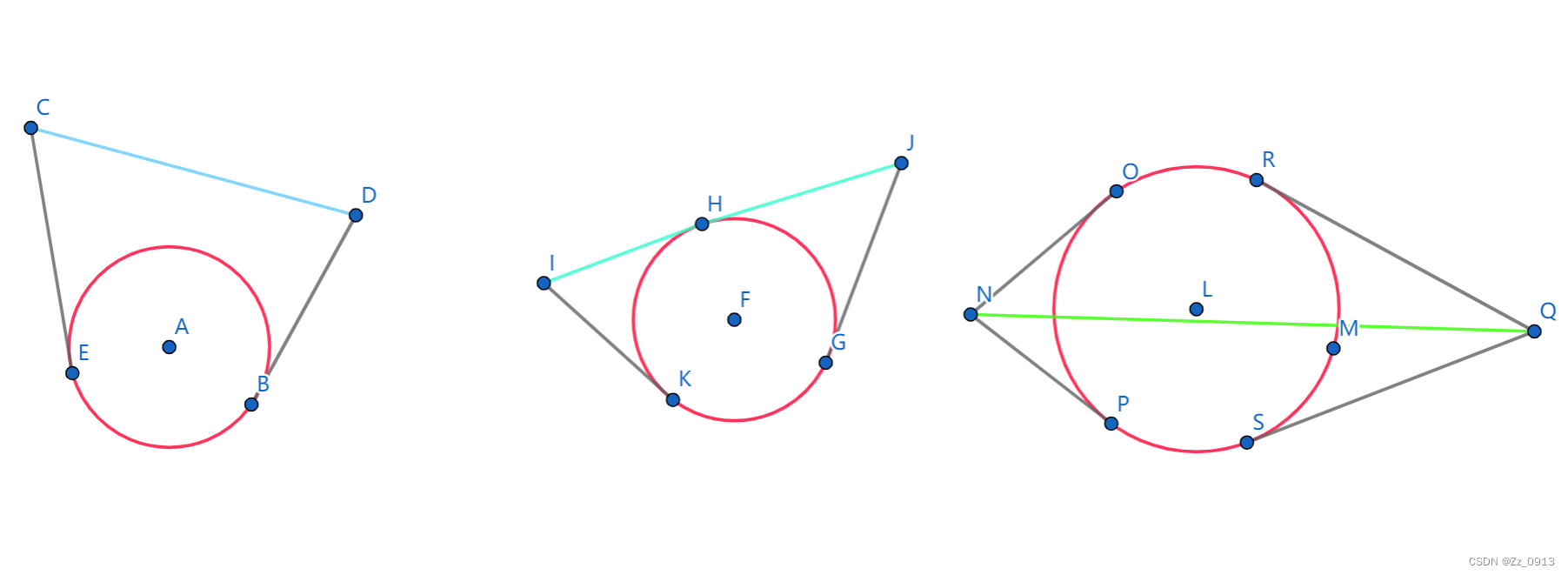
然后我们只需要先判断位置关系,然后用几何知识轻松求出面积即可~~~,如果对于面积的求法还有不会的uu们可以去看看我早期的一些计算几何基础讲解的博客~~~,接下来给出我的代码:
#include<bits/stdc++.h>
using namespace std;
const int QAQ = 0;
const int MAXN = 1005;
const double Eps = 1e-15;
const double pi = acos(-1.0);
double xa,ya,xb,yb,xp,yp,v,t;
struct Point{
double x,y;
Point(double x = 0,double y = 0) : x(x) , y(y) {}
}point[MAXN];
double sqr(double x) { return x * x;}
int Dcmp(double x,double y = 0) { if(fabs(x - y) < 0) return 0;if(x > y) return 1;if(x < y) return -1;}
typedef Point Vector;
Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}
Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}
Vector operator * (Vector Alpha,double x) { return Vector(Alpha.x * x,Alpha.y * x);}
Vector operator / (Vector Alpha,double x) { return Vector(Alpha.x / x,Alpha.y / x);}
bool operator < (const Point &Alpha,const Point &Beta)
{
if(Alpha.x == Beta.x) return Alpha.y < Beta.y;
return Alpha.x < Beta.x;
}
bool operator == (const Point &Alpha,const Point &Beta)
{
if(Dcmp(Alpha.x - Beta.x) == 0 && Dcmp(Alpha.y - Beta.y) == 0) return true;
return false;
}
struct Line{
Point v,p;
Line() {}
Line(Point v,Point p) : v(v) , p(p) {}
Point point(double t)
{
return v + (p - v) * t;
}
}line[MAXN];
double dis(Point Alpha,Point Beta) { return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));}
double Dot(Vector Alpha,Vector Beta) { return Alpha.x * Beta.x + Alpha.y * Beta.y;}
//点积
double Cross(Vector Alpha,Vector Beta) { return Alpha.x * Beta.y - Alpha.y * Beta.x;}
//叉积
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _;
cin>>_;
while(_--)
{
cin>>xp>>yp;
cin>>xa>>ya;
cin>>xb>>yb;
cin>>v>>t;
Point A = Point(xa,ya),B = Point(xb,yb),P = Point(xp,yp);
double ans = 0.0000000000000;
double d = v * t;//求出圆的半径
A.x = A.x - P.x,A.y = A.y - P.y;
B.x = B.x - P.x,B.y = B.y - P.y;//我们把圆平移到原点
P.x = 0,P.y = 0;
double AB = dis(A,B),AP = dis(A,P),BP = dis(B,P);
double APB = acos((sqr(AP) + sqr(BP) - sqr(AB)) / (2.0 * AP * BP));
double Theta = APB / 2.0,h = AP * cos(Theta);
double x = sqrt(sqr(AP) - sqr(h));
P.x = 0,P.y = 0;
A.x = -x,A.y = h,B.x = x,B.y = h;
if(Dcmp(h - d) >= 0)
{
double APC = acos(d / AP);//acos已知cos值求角度,建模的时候可以发现
double BPD = acos(d / BP);
double CPD = 2 * pi - 2 * Theta - APC - BPD;
double S = x * h + d * (sqrt(sqr(AP) - sqr(d))) + CPD * d * d / 2;
ans = S;
}else
{
if(Dcmp(AP - d) >= 0)
{
double S1 = sqrt(sqr(AP) - sqr(d)) * d * 2;
double APE = acos(d / AP);
double Sigma = 2 * pi - 4 * APE;
double S2 = Sigma * d * d / 2;
ans = S1 + S2;
} else ans = pi * sqr(d);
}
cout<<fixed<<setprecision(15)<<ans<<endl;
}//这只是我的一种写法,所以可以大家自己亲自建模一下,说不定有更巧妙的写法
return QAQ;
}T3:物理问题的建模


题目来源:
( Attachments - 2018 German Collegiate Programming Contest (GCPC 18) - Codeforces
那么本题是一道三维计算几何的建模题,考虑到了一个万有引力常量和地球的半径,大致题意就是卫星的位置与信号间的关系,那么这题也是笔者在早期赛时写出来的一道题,题干特别长加上这是一道三维计算几何题,很少人会在赛时投入去做,那么这题在正式比赛中做出来的人数相对来说少一些,不过总体来讲不是很难,那么经过两题的简单几何建模题的讲解后,本题的建模任务交给读者,这里我放上我的代码供大家参考,在我看来这题不如说更像一道物理的计算题🤔(三维球体的建模肯定是更加的有趣捏~):
#include<bits/stdc++.h>
using namespace std;
const int QAQ = 0;
double r = 6371;
double v = 299792.458;
double lo,la,x,y,z,f,p,diam,t;
const double pi = acos(-1.0);
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _;
cin>>_;
cin>>lo>>la;
la = la * pi / 180.0;
lo = lo * pi / 180.0;
while(_--)
{
cin>>f>>p>>diam>>t;
double xr,yr,zr,xs = diam,ys = 0,zs = 0;
t = t * 2.0 * pi;
p = p * pi / 180.0;
f = f * pi / 180.0;
z = r * sin(la);
x = r * cos(lo - f) * cos(la);
y = r * sin(lo - f) * cos(la);
double a,b,c,d;
a = x,b = y,c = z;
d = -(x * x + y * y + z * z);
xr = cos(t) * xs - sin(t) * ys;
yr = sin(t) * xs + cos(t) * ys;
zr = zs,xs = xr;
ys = cos(p) * yr - sin(p) * zr;
zs = sin(p) * yr + cos(p) * zr;
if(d * (a * xs + b * ys + c * zs + d) > 0) cout<<"no signal"<<"\n";
else cout<<fixed<<setprecision(8)<<sqrt((x - xs) * (x - xs) + (y - ys) * (y - ys) + (z - zs) * (z - zs)) / v<<"\n";
}
return QAQ;
}
OK,那么对于这第一类的计算几何题,做法十分明确,主要考察的是一个建模和几何的基础知识,我在这里在放几题供读者们练习:
Problem - 452B - Codeforces
Problem - O - Codeforces
Problem - P - Codeforces
Problem - F - Codeforces
Problem - B - Codeforces
Problem - D - Codeforces
Problem - F - Codeforces
---------------------------------------------------- 我是一条分割线() ----------------------------------------------------
第二类 : 几何问题同时涉及一些XCPC基本算法的较难题
我来讲讲这类题的能够涉及到的一些算法,一般求路径可能会涉及最短路算法,求一些最优方案会涉及到随机增量法及其变种,还有动态规划(一般常用的是状态压缩)等等
T1:随机增量的应用
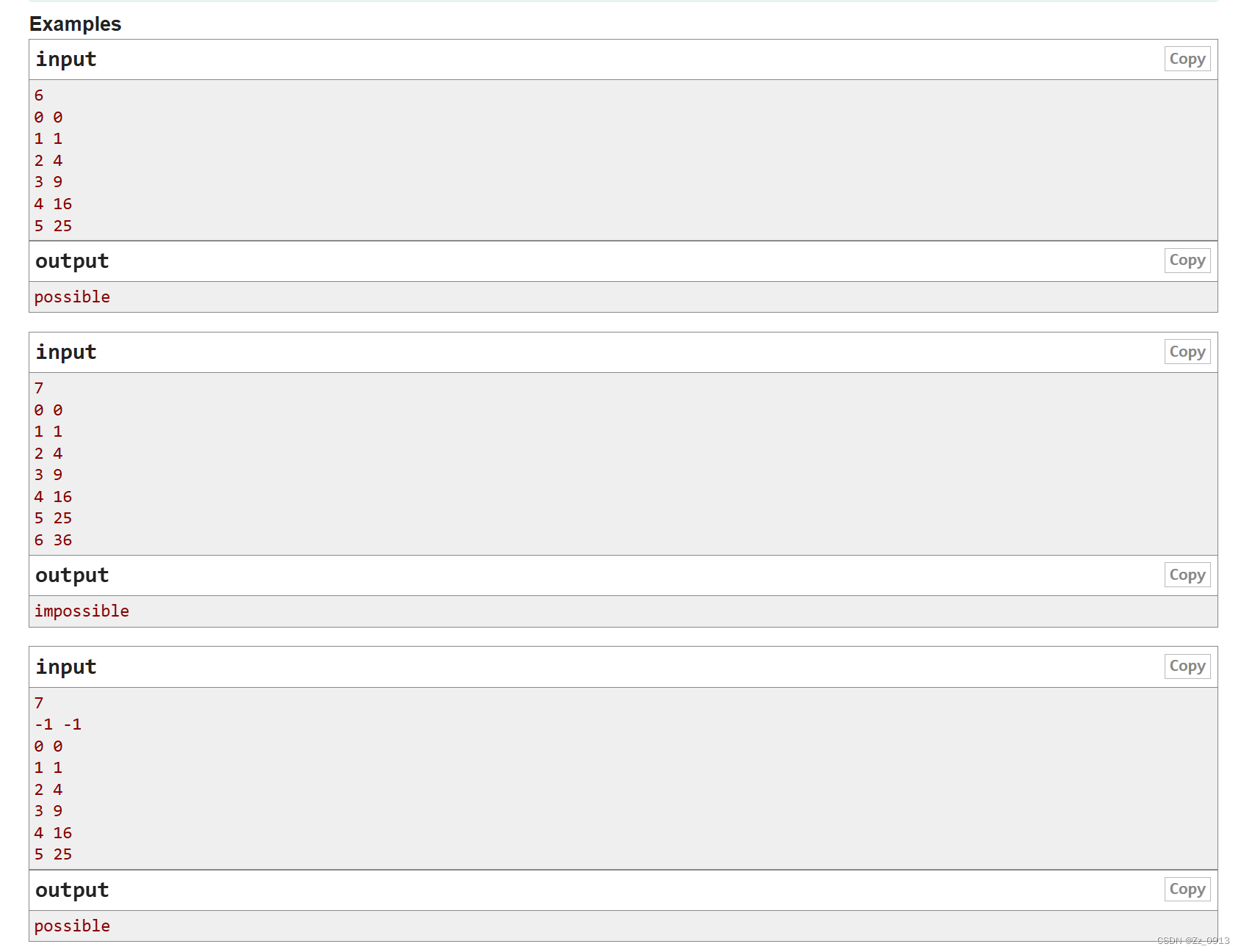
题目来源:Problem - B - Codeforces
题意: 给你二维平面上的n个点,询问你是否至多只需要三条直线就能将其全部连结.
题解:关于这题笔者联想到了一道板题,也就是最小圆覆盖,那题是给我们n个点找到一个半径最小的圆来覆盖平面上所有的点,这两道题有什么关联呢,那就是两者都是判断几何图形的一个覆盖性质,对于这类题我们一般可以尝试使用随机增量法的一个运用,随机增量法是啥(见以前的博客),举个例子?
/*①随意找一点作为初始解,并用随洗牌法打乱半平面顺序。
②如果没有型的半平面可以加入,输出有解。否则转③。
③加入一个新的半平面,如果当前点在半平面上,转②,否则转④。
④对于新加入的第k+1条直线,用前个半平面去截,如果截后有剩余,保留
剩余部分最下方一点,转②,否则输出无解。*/
👆这是某道计算几何的采用随机增量法的一个算法流程,所以我们可以借鉴一下,把所给出的这一题也设计一个类似的算法求解,首先我们建模:

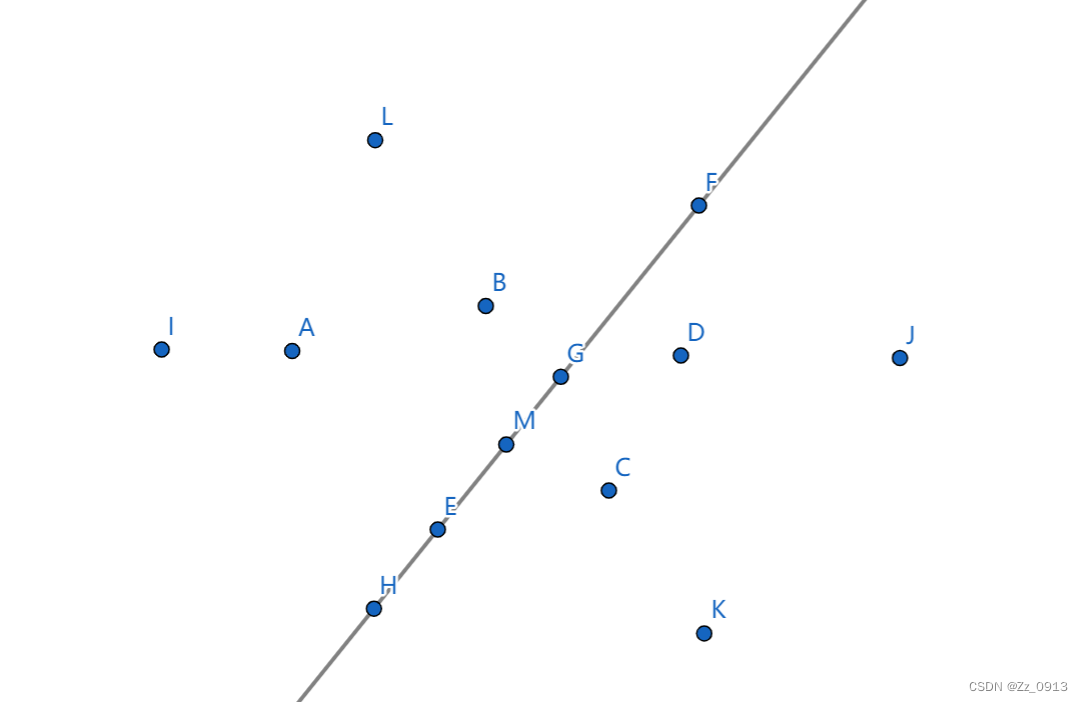
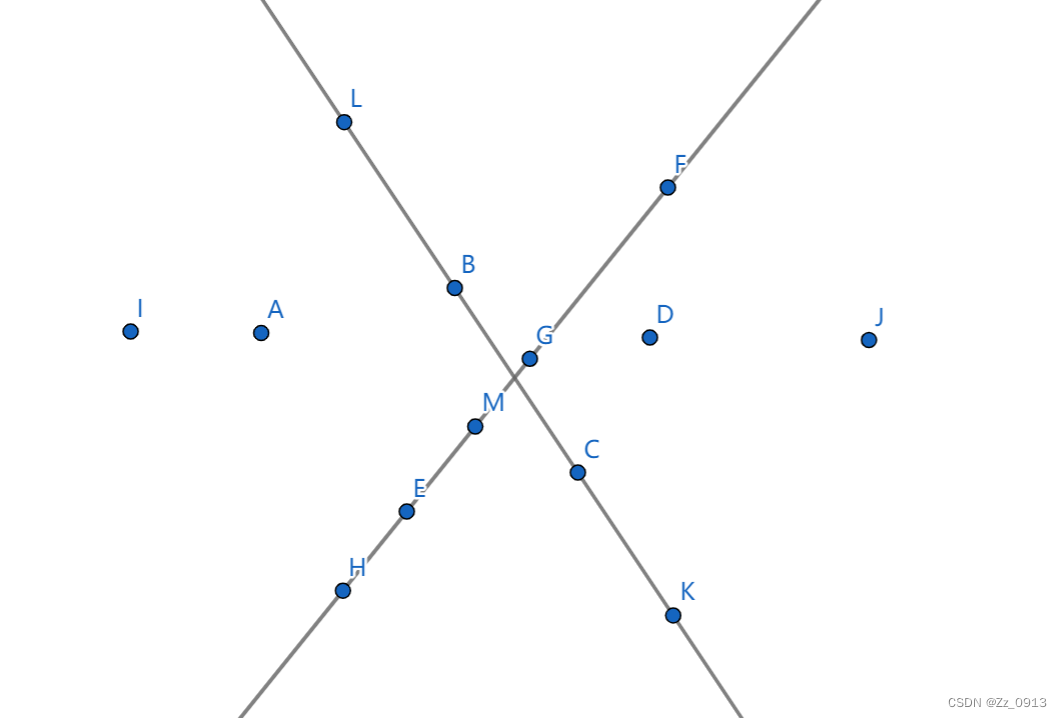
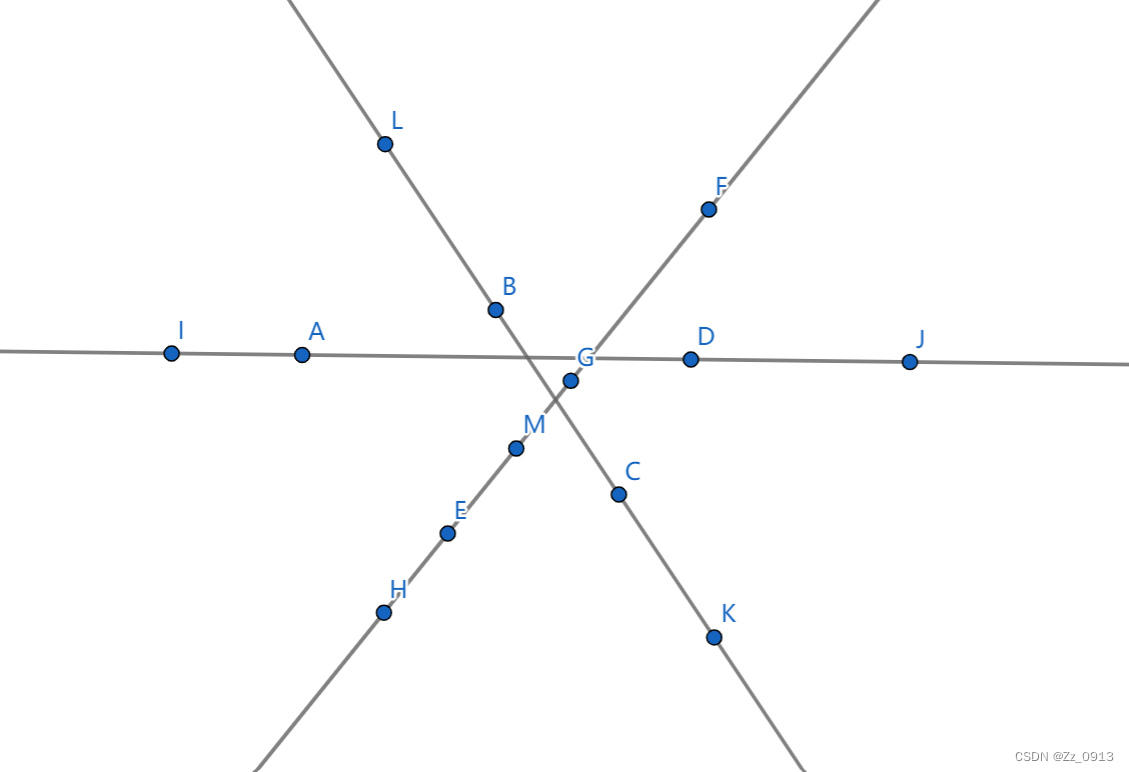
👆,然后笔者是这样设计算法的:
1.首先点数小于等于3的情况特判为成立.
2.然后对于其它情况,我们先挑选四个点,枚举答案的直线,也就是枚举四个点中的两个,每次把直线上的点删除,剩下的点中挑3个点,然后按四个点的情况枚举并删点,接着是剩余两个点的情况一样的进行删点,那么这样我们就有了三条直线,我们判断剩余是否还存在点不在这三条直线上,最后如果有成立的方案存在,那么这些点就是满足条件的。
👆:这部分的实现很明显用dfs非常的方便
推广:假如是让我们判断k条直线能否连接所有的点呢?
-----------那么也是一样的,我们首先枚举K个点中的两两直线,删点,然后是K - 1个,删点,一直到枚举两个点为止确定所有的直线,所以这个的时间复杂度是阶乘级别的,k就不能太大啦。在这题中的时间复杂度可以精确的算出,在K = 3时为 : O(18*n)
OK,接下来给大家献上我的代码,可以供参考👇:
#include<bits/stdc++.h>
using namespace std;
const double Eps = 1e-15;
const int QAQ = 0;
const int MAXN = 2e4 + 10;
int n,tong[MAXN],t,e,a[10],b[10],tong1[MAXN];
int t1,t2;
int x,y;
bool p;
struct Point{ int x,y; };
vector<Point> point;
bool check(Point x,Point y,Point z)
{
if((y.x - z.x) * (x.y - y.y) == (x.x - y.x) * (y.y - z.y))
return true;
return false;
}
void dfs(vector<Point> a,int k)//有一些点和要挑出的点的个数为K
{
if(a.size() <= k)
{
p = true;
return;
}
for(int i = 0;i <= k;i++)
for(int j = i + 1;j <= k;j++)//两点确定一条直线
{
vector<Point> b;
for(auto l : a)
if(!check(a[i],a[j],l)) b.push_back(l);
dfs(b,k - 1);
}
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _;
_ = 1;
while(_--)
{
cin>>n;
for(int i = 1;i <= n;i++)
{
cin>>x>>y;
point.push_back({x,y});
}
p = false;
dfs(point,3);//K= 3
if(p) cout<<"possible"<<endl;else cout<<"impossible"<<endl;
}
return QAQ;
}
T2:与最短路算法的结合
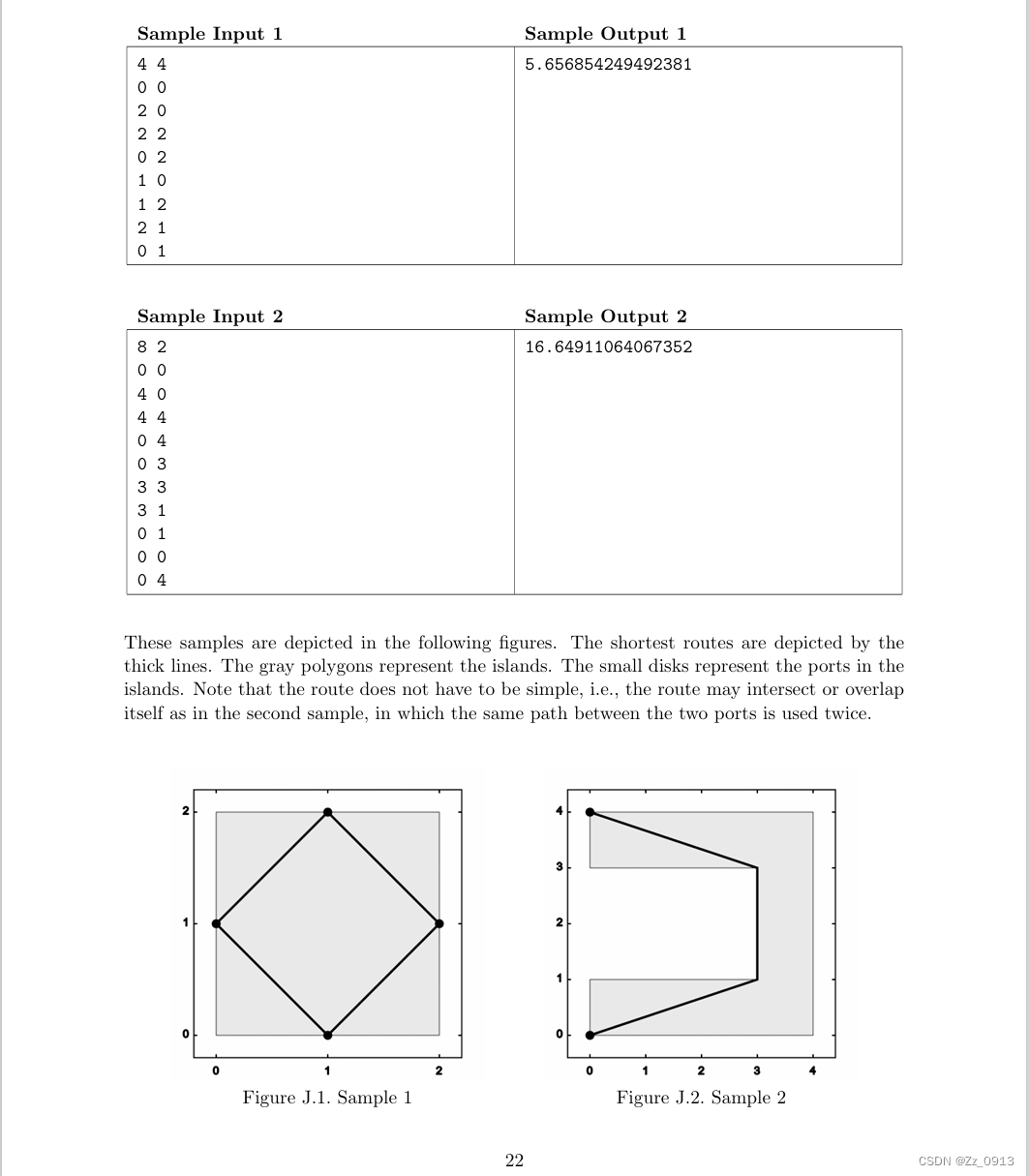
题目来源:Problem - J - Codeforces
题意: 给你一个任意多边形的一些顶点,以及多边形的边上的一些顶点,希望你能求出一条线路,满足这条线路经过所有的顶点并且任何线路的部分只能在多边形上,求其最短的长度。
这道题目的意思就相当明确了,建模十分好建: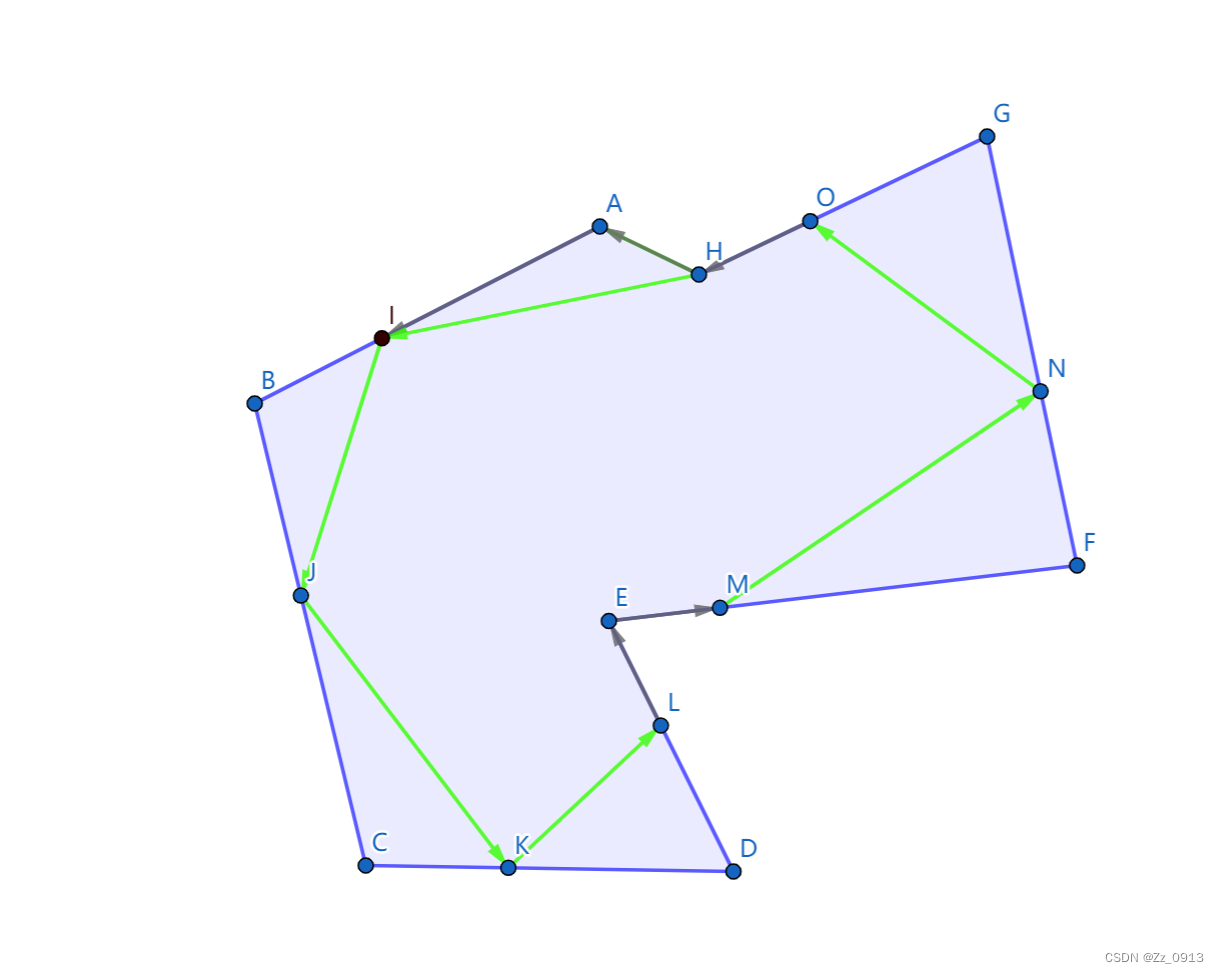
这样一画,那么这题的模型就出来了,大致的一个思路就是把点的一个圆周顺序排列出来,这里需要一个排序操作,然后建立点与点之间的一个距离关系,这些距离关系构成了一个边集,然后我们对这个边集跑一遍最短路即可。那么难点在哪里呢?
难点一:多边形的凹凸性不定,所以某两点的距离如图中的L和M不能直接连接,最佳方案而是LE+EM这两条边的和,所以判断一个半平面交是个难点。
难点二:那么为了方便计算,我们不止需要将上面的点与点建边,而是要把多边形的顶点加入,然后我们要通过半平面交筛选掉那些不合法的边集即可。
具体的流程: 连边->筛边->建图->FLoyed更新距离->点的时针顺序排序->Floyed求值
接下来就给出笔者的赛时代码,可供大家参考👇:
#include<bits/stdc++.h>
#define int long long
#define Alex ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
using namespace std;
const int mod = 998244353;
const int QAQ = 0;
const double Eps = 1e-9;
vector<int> V[555];
vector<int> G;
double dis[555][555];
double x,y;
int n,m,nn,k,gh;
double ans;
int Sign(double x)
{
if(fabs(x) <= Eps) return 0;
if(x == 0) return 0;
if(x > 0) return 1;
if(x < 0) return -1;
}
double sqr(double x)
{
return x * x;
}
struct Point{
double x,y;
Point(double x = 0,double y = 0) : x(x) , y(y) {}
};
Point Nodes[555];
typedef Point Vector;
Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}
Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}
double operator * (Vector Alpha,Vector Beta)
{
return Alpha.x * Beta.x + Alpha.y * Beta.y;
}
double operator ^ (Vector Alpha,Vector Beta)
{
return (Alpha.x * Beta.y - Alpha.y * Beta.x);
}
double operator | (Vector Alpha,Vector Beta)
{
return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));
}
bool operator == (Vector Alpha,Vector Beta)
{
return Sign(Alpha.x - Beta.x) == 0 && Sign(Alpha.y - Beta.y) == 0;
}
bool OnSegment(Point x,Point y,Point z)
{
return Sign((y - x) ^ (z - x)) == 0
&& Sign((y - x) * (z - x)) > 0
&& Sign((x - y) * (z - y)) > 0;
}//判断点在线上否?
int Intersection(Point x)
{
int ans = 0;
for(int i = 1;i <= nn;i++)
{
int u = i,v = i % nn + 1;
if((OnSegment(Nodes[u],Nodes[v],x)) || Nodes[u] == x) return 1;
double gh = (Nodes[v] - Nodes[u]) ^ (x - Nodes[u]);
if(gh > 0 && Nodes[u].y < x.y && x.y <= Nodes[v].y) ans = ans ^ 1;
if(gh < 0 && Nodes[u].y >= x.y && x.y > Nodes[v].y) ans = ans ^ 1;
}
return ans;
}//求交,主要用到的是一个关键的叉积运算
bool ok(int x,int y)
{
for(int i = 1;i <= nn;i++)
{
int u = i,v = i % nn + 1;
double A = (Nodes[x] - Nodes[u]) ^ (Nodes[v] - Nodes[u]);
double B = (Nodes[y] - Nodes[u]) ^ (Nodes[v] - Nodes[u]);
double C = (Nodes[u] - Nodes[x]) ^ (Nodes[y] - Nodes[x]);
double D = (Nodes[v] - Nodes[x]) ^ (Nodes[y] - Nodes[x]);
if((Sign(A) * Sign(B) < 0) && (Sign(C) * Sign(D) < 0)) return false;
if(OnSegment(Nodes[x],Nodes[y],Nodes[i])) return false;
}
Vector ljh = Nodes[x] + Nodes[y];
ljh.x = ljh.x / 2.00;
ljh.y = ljh.y / 2.00;
if(Intersection(ljh)) return true;else return false;
}//这里的判断方法我们采用的是求半平面交,这是一个难点,不过有一个计算几何板子就能解决
inline bool cmp(int x,int y)
{
return dis[x][gh] < dis[y][gh];
}
signed main()
{
Alex;
int _;
_ = 1;
while(_--)
{
cin>>n>>m;
k = 0;
for(int i = 1;i <= n;i++)
{
k++;
cin>>Nodes[k].x>>Nodes[k].y;
}
for(int i = 1;i <= m;i++)
{
k++;
cin>>Nodes[k].x>>Nodes[k].y;
for(int j = 1;j <= n;j++)
{
int u = j,v = j % n + 1;
if(OnSegment(Nodes[u],Nodes[v],Nodes[k]) || Nodes[u] == Nodes[k])
V[j].push_back(k);
}
}//建边
nn = n;
n = k;
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
{
if(i == j) dis[i][j] = dis[j][i] = 0;
else dis[i][j] = INT_MAX;
}
for(int i = 1;i <= n;i++)
for(int j = i + 1;j <= n;j++)
{
if(ok(i,j) == false) continue;
dis[i][j] = dis[j][i] = fmin(dis[i][j],Nodes[i] | Nodes[j]);
}//筛边
for(int k = 1;k <= n;k++)
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
dis[i][j] = fmin(dis[i][j],dis[i][k] + dis[k][j]);//用FLoyed更新距离
k = 0;
for(int i = 1;i <= nn;i++)
{
gh = i;
sort(V[i].begin(), V[i].end(),cmp);
for(auto v : V[i])
{
k++;
G.push_back(v);
}
}//点的排序
double ans = 0.00;
for(int i = 0;i <= k - 1;i++)
ans = ans + dis[G[i]][G[(i + 1) % k]];//结论
cout<<fixed<<setprecision(15)<<ans<<'\n';
}
return QAQ;
}
T3:几何中的数论知识点考察

题目来源:Problem - J - Codeforces
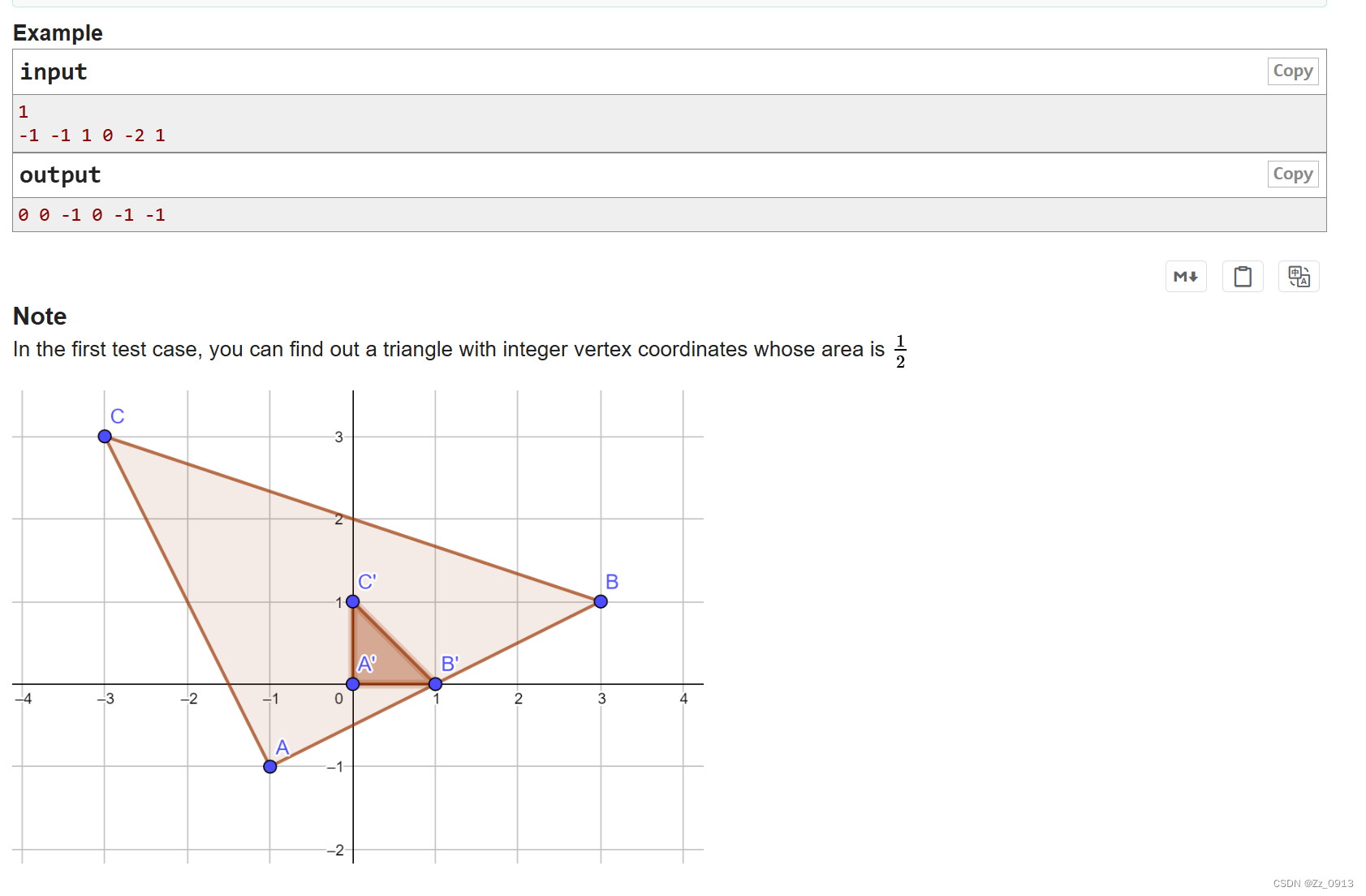
题意: 给你一个顶点都为整点的三角形,让你求出一个面积最小的整点三角形,使其与给出的三角形相似。
emmmmm,这题笔者在VP的时候没写出来啊,看似简单实则很有难度的,但是这题我们不需要建模,我们只需要知道最小的那个相似三角形,需要满足什么条件?那就是三边都与给定三角形都成比例,且一定为两个完全平方数的和,也就是我们常说的勾股数,所以说我们只需要求出一个满足条件的比例即可,对于勾股数,我们也可以找到相应的结论:
有了上述的理论基础,我们就可以认定这个算法是可以实现的了,不过貌似这题也就跟计算几何的关系不是很大了,它更是偏向于了一个数论中的结论,所以我这里给出一个可行的代码:
#include<bits/stdc++.h>
#define Alex ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define fors(i, a, b) for(int i = (a); i < (b); ++i)
#define all(vec) vec.begin(),vec.end()
using namespace std;
#define P complex<ll>
ll diva(ll a, ll b)
{
ll d = a / b, r = a % b;
if(2 * r >= b)d++;
if(2 * r <= -b)d--;
return d;
}
P div(P a, P b)
{
ll d = norm(b);
a = a * conj(b);
return {diva(a.real(), d), diva(a.imag(), d)};
}
P gcd(P a, P b)
{
if(norm(b) == 0) return a;
return gcd(b, a - div(a,b) * b);
}
int main()
{
Alex;
int T;
cin>>T;
while(T--)
{
ll x1,y1,x2,y2,x3,y3;
cin>>x1>>y1>>x2>>y2>>x3>>y3;
P a = P(x2 - x1, y2 - y1), b = P(x3 - x1, y3 - y1);
P g = gcd(a, b);
a = div(a, g);
b = div(b, g);
cout<<"0 0 "<<a.real()<<" "<<a.imag()<<" "<<b.real()<<" "<<b.imag()<<endl;
}
return 0;
}
那么为了防止博文太长了(其实是笔者累啦),这个第二类计算几何我打算再放六个,然后第三类的强度比较大,因此,我在这里郑重决定,把剩下的内容放入<<计算几何系列——XCPC中计算几何一些题型杂谈(中/下)>>中去doge,不过在这里我也放几题有趣的思考题,大家可以去试试捏~:(下一章的内容要好好考虑,大概在2024年6.30号之前会出~)
如果有什么不会的地方可以在Codeforces上找用户Healexr,欢迎来一起讨论问题哈~



























 5268
5268

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








