吴恩达《深度学习专项》笔记+代码实战（二）：简单的神经网络——逻辑回归

这堂课要学习的是逻辑回归——一种求解二分类任务的算法。同时，这堂课会补充实现逻辑回归必备的数学知识、编程知识。学完这堂课后，同学们应该能够用Python实现一个简单的小猫辨别器。

前排提示：本文篇幅较长。如果想看本文的精简版，欢迎移步我在其他地方发的文章.

学习提示

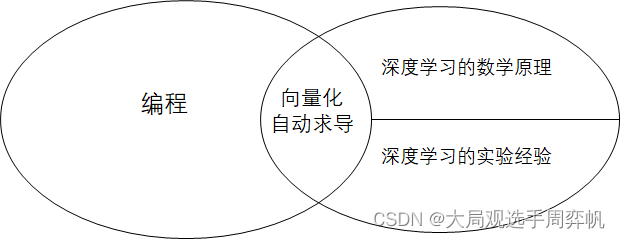
如上图所示，深度学习和编程，本来就是相对独立的两块知识。

深度学习本身的知识包括数学原理和实验经验这两部分。深度学习最早来自于数学中的优化问题。随着其结构的复杂化，很多时候我们解释不清为什么某个模型性能更高，只能通过重复实验来验证模型的有效性。因此，深度学习很多情况下变成了一门“实验科学”。

深度学习中，只有少量和编程有关系的知识，比如向量化计算、自动求导器等。得益于活跃的开源社区，只要熟悉了这些少量的编程技巧，人人都可以完成简单的深度学习项目。但是，真正想要搭建一个实用的深度学习项目，需要完成大量“底层”的编程工作，要求开发者有着广泛的编程经验。

通过上吴恩达老师的课，我们应该能比较好地掌握深度学习的数学原理，并且了解深度学习中少量的编程知识。而广泛的编程经验、修改模型的经验，这些都是只上这门课学不到的。

获取修改模型的经验这项任务过于复杂，不太可能短期学会，几乎可以作为研究生的课题了。而相对而言，编程的经验就很好获得了。

我的系列笔记会补充很多编程实战项目，希望读者能够通过完成类似的编程项目，在学习课内知识之余，提升广义上的编程能力。比如在这周的课程里，我们会用课堂里学到的逻辑回归从头搭建一个分类器。

课堂笔记

本节课的目标

在这节课里，我们要完成一个二分类任务。所谓二分类任务，就是给一个问题，然后给出一个“是”或“否”的回答。比如给出一张照片，问照片里是否有一只猫。

这节课中，我们用到的方法是逻辑回归。逻辑回归可以看成是一个非常简单的神经网络。

符号标记

从这节课开始，我们会用到一套统一的符号标记：

$(x,y)$ 是一个训练样本。其中，$x$ 是一个长度为 $n_x$ 的一维向量，即 $x\in {\mathcal{R}}^{n_x}$。$y$ 是一个实数，取0或1，即 y ∈ { 0 , 1 } y \in \{0, 1\} y∈{ 0,1}。取0表示问题的的答案为“否”，取1表示问题的答案为“是”。

这套课默认读者对统计机器学习有基本的认识，似乎没有过多介绍训练集是什么。在有监督统计机器学习中，会给出训练数据。训练数据中的每一条训练样本包含一个“问题”和“问题的答案”。神经网络根据输入的问题给出一个自己的解答，再和正确的答案对比，通过这样一个“学习”的过程来优化解答能力。

对计算机知识有所了解的人会知道，在计算机中，颜色主要是通过RGB（红绿蓝）三种颜色通道表示。每一种通道一般用长度8位的整数表示，即用一个0~255的数表示某颜色在红、绿、蓝上的深浅程度。这样，一个颜色就可以用一个长度为3的向量表示。一幅图像，其实就是许多颜色的集合，即许多长度为3的向量的集合。颜色通道，再算上某颜色所在像素的位置$(x,y)$，图像就可以看成一个3维张量$I\in {\mathcal{R}}^{H\times W\times 3}$，其中$H$是图像高度，$W$是图像宽度，$3$是图像的通道数。在把图像输入逻辑回归时，我们会把图像“拉直”成一个一维向量。这个向量就是前面提到的网络输入$x$，其中$x$的长度$n_x$满足$n_x=H\times W\times 3$。这里的“拉直”操作就是把张量里的数据按照顺序一个一个填入新的一维向量中。

其实向量就是一维的，但我还是很喜欢强调它是“一维”的。这是因为在计算机中所有数据都可以看成是数组（甚至C++的数组就叫vector)。二维数组不过是一维数组的数组，三位数组不过是二维数组的数组。在数学中，为了方便称呼，把一维数组叫“向量”，二维数组叫“矩阵”，三维及以上数组叫“张量”。其实在我看来它们之间只是一个维度的差别而已，叫“三维向量”、“一维张量”这种不是那么严谨的称呼也没什么问题。

实际上，我们有很多个训练样本。样本总数记为$m$。第$i$个训练样本叫做$(x^{(i)},y^{(i)})$。在后面使用其他标记时，也会使用上标$(i)$表示第$i$个训练样本得到的计算结果。

所有输入数据的集合构成一个矩阵（其中每个输入样本用列向量的形式表示，这是为了方便计算机的计算）：

$$X=\left[\begin{array}{cccc}|& |& & |\\ x^{(1)}& x^{(2)}& ...& x^{(m)}\\ |& |& & |\end{array}\right],X\in {\mathcal{R}}^{n_x\times m}$$

同理，所有真值也构成集合 $Y$:

$$Y=\left[\begin{array}{cccc}{y}^{(1)}& y^{(2)}& ...& y^{(m)}\end{array}\right],Y\in {\mathcal{R}}^m$$
由于每个样本$y^{(i)}$是一个实数，所以集合$Y$是一个向量。

逻辑回归的公式描述

逻辑回归是一个学习算法，用于对真值只有0或1的“逻辑”问题进行建模。给定输入$x$,逻辑回归输出一个$\hat{y}$。这个$\hat{y}$是对真值$y$的一个估计，准确来说，它描述的是$y=1$的概率，即$\hat{y}=P(y=1|x)$

逻辑回归会使用一个带参数的函数计算$\hat{y}$。这里的参数包括$w\in {\mathcal{R}}^{n_x},b\in \mathcal{R}$。

说起用于拟合的函数，最容易想到的是线性函数$w^{T}x+b$（即做点乘再加$b$： $w^{T}x+b=({\Sigma }_{i=1}^{n_x}{w}_i{x}_i)+b$ ）。但线性函数的值域是$(-\infty ,+\infty )$（即全体实数$\mathcal{R}$），概率的取值是$[0,1]$。我们还需要一个定义域为$\mathcal{R}$，值域为$[0,1]$，把线性函数映射到$[0,1]$上的一个函数。

逻辑回归中，使用的映射函数是sigmoid函数$\sigma$,它的定义为：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$

这个函数可以有效地完成映射，它的函数图像长这个样子：

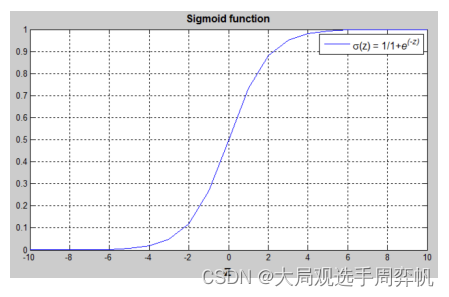
这里不用计较为什么使用这个函数，只需要知道这个函数的趋势：$x$越小，$\sigma (x)$越靠近0；$x$越大，$\sigma (x)$越靠近1。

也就是说，最终的逻辑回归公式长这个样子：$\hat{y}=$