DTW算法详解
1.DTW
1.1 时序相似度
在时间序列数据中,一个常见的任务是比较两个序列的相似度,作为分类或聚类任务的基础。那么,时间序列的相似度应该如何计算呢?
“ 经典的时间序列相似性度量方法总体被分为两 类: 锁步度量(lock-step measures) 和弹性度量(elastic measures) . 锁步度量是时间序列进行 “一对一”的比 较; 弹性度量允许时间序列进行 “一对多”的比较.
——《时间序列数据挖掘的相似性度量综述》
”最简单的相似度计算方法可能是计算两个时间序列的欧氏距离。欧氏距离属于锁步度量
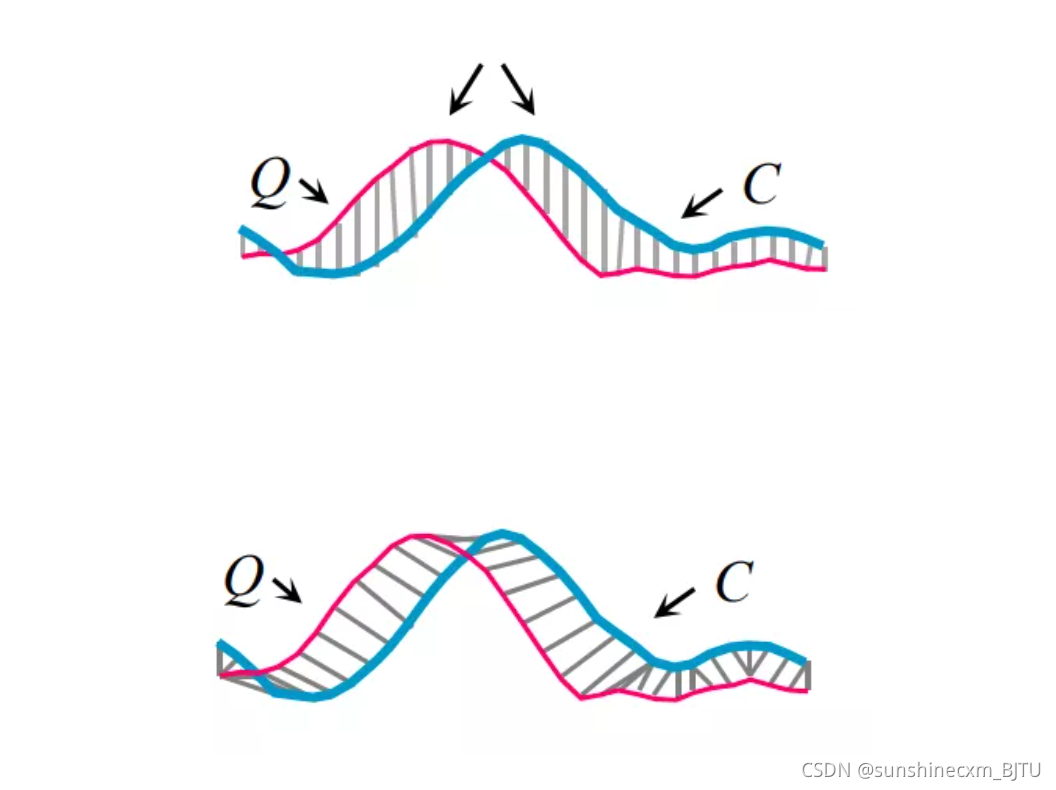
假设有两个时间序列,Q和C,如果直接用欧氏距离计算相似度的话,如果存在时间步不对齐,序列长短不一等问题…
如上图1所示,如果序列长短不一,或时间步不对齐的时候,欧氏距离是无法有效计算两个时间序列的距离,特别是在峰值的时候。图2则是DTW算法,首先将其中一个序列进行线性放缩进行某种“扭曲”操作,以达到更好的对齐效果,可以存在一对多mapping的情况,适用于复杂时间序列,属于弹性度量
1.2 DTW算法
动态时间规整在60年代由日本学者Itakura提出,用于衡量两个长度不同的时间序列的相似度。把未知量伸长或缩短(压扩),直到与参考模板的长度一致,在这一过程中,未知序列会产生扭曲或弯折,以便其特征量与标准模式对应
首先假设有两条序列 Q QQ 和 C CC,他们的长度分别是 n nn 和 m mm
Q = q 1 , q 2 , . . . , q n Q=q_1,q_2,...,q_nQ=q1,q2,...,qn
C = q 1 , q 2 , . . . , q n C=q_1,q_2,...,q_nC=q1,q2,...,qn用一个 m × n m\times nm×n 矩阵来对比两个序列,warping路径会穿越这个矩阵,warping路径的第 k kk 个元素表示为w k = ( i , j ) k w_k=(i,j)_kwk=(i,j)k ,横纵代表的是两个序列对齐的点
约束条件1)边界条件:w 1 = ( 1 , 1 ) w_1=(1,1)w1=(1,1) 和w k = ( m , n ) w_k=(m,n)wk=(m,n),表示两条序列首尾必须匹配,各部分的先后次序匹配。
2)连续性: 如果w k = ( a , b ) w_k=(a,b)wk=(a,b)且w k − 1 = ( a ′ , b ′ ) w_k-1=(a',b')wk−1=(a′,b′),则必须满足 a − a ′ ≤ 1 a-a' \leq 1a−a′≤1
且 b − b ′ ≤ 1 b-b' \leq 1b−b′≤1。这条约束表示在匹配过程中多对一和一对多的情况只能匹配周围一个时间步的的情况,也就是不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q QQ和C CC中的每个坐标都在wraping路径中出现。3)单调性: 如果 w k − 1 = ( a ′ , b ′ ) w_k-1=(a',b')wk−1=(a′,b′),且w k = ( a , b ) w_k=(a,b)wk=(a,b),则必须满足a − a ′ ≥ 0 a-a' \geq 0a−a′≥0
且b − b ′ ≥ 0 b-b' \geq 0b−b′≥0,表示warping路径一定是随时间单调递增的。满足以上约束条件的warping路径有很多,所以问题的本质是最优化问题——找出最优warping路径。
解法思路是通过动态规划算法,数学语言描述为:
【举例】
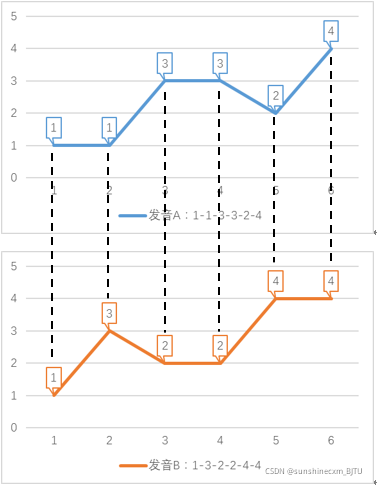
DTW最初用于识别语音的相似性。我们用数字表示音调高低,例如某个单词发音的音调为1-3-2-4。现在有两个人说这个单词,一个人在前半部分拖长,其发音为1-1-3-3-2-4;另一个人在后半部分拖长,其发音为1-3-2-2-4-4。现在要计算1-1-3-3-2-4和1-3-2-2-4-4两个序列的距离(距离越小,相似度越高)。因为两个序列代表同一个单词,我们希望算出的距离越小越好,这样把两个序列识别为同一单词的概率就越大。
先用传统方法计算两个序列的欧几里得距离,即计算两个序列各个对应的点之间的距离之和。
距离之和
= |A(1)-B(1)| + |A(2)-B(2)| + |A(3)-B(3)| + |A(4)-B(4)| + |A(5)-B(5)| + |A(6)-B(6)|
= |1-1| + |1-3| + |3-2| + |3-2| + |2-4| + |4-4|
= 6
如果我们允许序列的点与另一序列的多个连续的点相对应(相当于把这个点所代表的音调的发音时间延长),然后再计算对应点之间的距离之和。如下图:B(1)与A(1)、A(2)相对应,B(2)与A(3)、A(4)相对应,A(5)与B(3)、B(4)相对应,A(6)与B(5)、B(6)相对应。
这样的话,距离之和
= |A(1)-B(1)| + |A(2)-B(1)| + |A(3)-B(2)| + |A(4)-B(2)| + |A(5)-B(3)| + |A(5)-B(4)| + |A(6)-B(5)| + |A(6)-B(6)|
= |1-1| + |1-1| + |3-3| + |3-3| + |2-2| + |2-2| + |4-4| + |4-4|
= 0我们把这种“可以把序列某个时刻的点跟另一时刻多个连续时刻的点相对应”的做法称为时间规整(Time Warping)。
现在我们用一个6*6矩阵M表示序列A(1-1-3-3-2-4)和序列B(1-3-2-2-4-4)各个点之间的距离,M ( i , j ) M(i, j)M(i,j) 等于A的第i个点和B的第j个点之间的距离,即
我们看到传统欧几里得距离里对应的点:
- A(1)-B(1)
- A(2)-B(2)
- A(3)-B(3)
- A(4)-B(4)
- A(5)-B(5)
- A(6)-B(6)
它们正好构成了对角线,对角线上元素和为6。
时间规整的方法里,对应的点为:
- A(1)A(2)-B(1)
- A(3)A(4)-B(2)
- A(5)-B(3)B(4)
- A(6)-B(5)B(6)
这些点构成了从左上角到右下角的另一条路径,路径上的元素和为0。
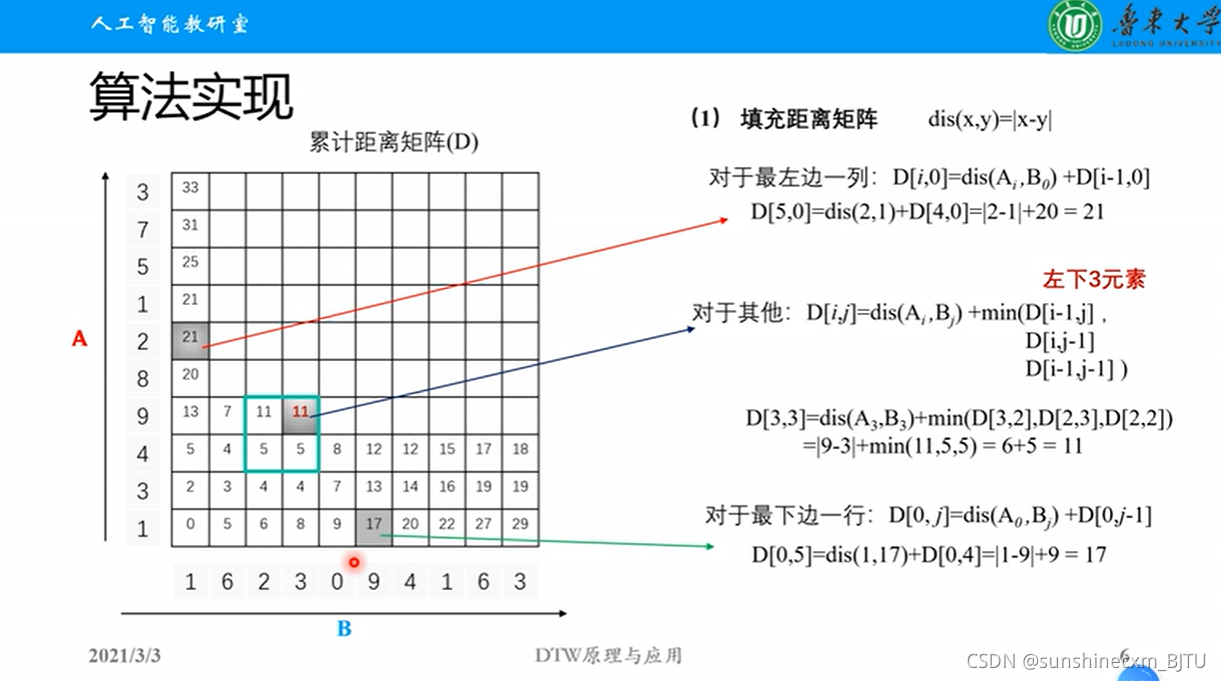
因此,DTW算法的步骤为:
- 计算两个序列各个点之间的距离矩阵。
- 寻找一条从矩阵左上角到右下角的路径,使得路径上的元素和最小。
我们称路径上的元素和为路径长度。那么如何寻找长度最小的路径呢?
矩阵从左上角到右下角的路径长度有以下性质:
- 当前路径长度 = 前一步的路径长度 + 当前元素的大小
- 路径上的某个元素(i, j),它的前一个元素只可能为以下三者之一:
a) 左边的相邻元素 (i, j-1)
b) 上面的相邻元素 (i-1, j)
c) 左上方的相邻元素 (i-1, j-1)假设矩阵为M,从矩阵左上角(1,1)到任一点(i, j)的最短路径长度为Lmin(i, j)。那么可以用递归算法求最短路径长度:
起始条件:
递推规则:
递推规则这样写的原因是因为当前元素的最短路径必然是从前一个元素的最短路径的长度加上当前元素的值。前一个元素有三个可能,我们取三个可能之中路径最短的那个即可。参考文献
https://www.bilibili.com/video/BV12r4y1A7mT?share_source=copy_web
https://zhuanlan.zhihu.com/p/43247215
https://it.wikipedia.org/wiki/Dynamic_time_warping
fastdtw 包计算
https://pypi.org/project/fastdtw/
from fastdtw import fastdtw
from scipy.spatial.distance import euclidean
x = np.array([1, 2, 3, 3, 7])
y = np.array([1, 2, 2, 2, 2, 2, 2, 4])
distance, path = fastdtw(x, y, dist=euclidean)
print(distance)
print(path)
# 5.0
# [(0, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 5), (3, 6), (4, 7)]







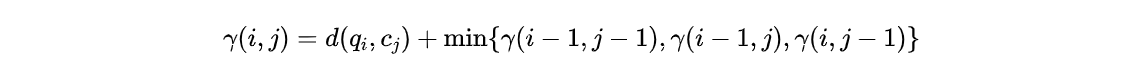

























 779
779

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








