卷积神经网络（CNN）

小黄要当程序员

已于 2023-09-14 10:35:37 修改

阅读量1.6k

点赞数 1

分类专栏：神经网络文章标签： cnn 人工智能深度学习神经网络机器学习算法卷积神经网络

于 2023-09-07 09:29:54 首次发布

本文链接：https://blog.csdn.net/a2333333_/article/details/132318483

版权

神经网络专栏收录该内容

5 篇文章

订阅专栏

本文围绕卷积神经网络展开，指出全连接前馈网络处理高维数据时参数量巨大的问题。介绍了图片数据的表示、局部不变性和感受野，阐述了一维和二维卷积的原理、特点及相关参数，还说明了网络构成，包括全连接与卷积对比、汇聚层作用及卷积神经网络典型结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

全连接前馈网络有十分强大的能力，但也正是由于它两层之间的神经元两两连接，这也就造成了一个问题，对于高维数据而言，参数量是十分巨大的
以一张480P的640*480的三通道标清图片为例，其输入数据便有640*480*3=921,600个，而训练所涉及的图片又有成千上万，训练过程就显得十分复杂

一、从数据到图片

对于图片数据而言，我们常以[C,H,W]来表示；其中C代表通道数，彩色图片为3，黑白则为1；H,W为图片的宽高，每一个单位代表一个像素点；

1.1局部不变性

人类识别图片内容是一个复杂且抽象的过程，把一张图片进行翻转，平移，裁剪一般是不影响识别的；（左图由右图变换而来，人类仍然可以识别是同一类

显然，我们以往接触的常规数据并没有如此强大的局部不变性，全连接网络也不支持特征的交换。

我们在使用图片数据进行训练时常把图像进行翻转，平移，裁剪等一系列操作，期望机器能学习到不容易受干扰的特征识别的能力，我们称这种做法为数据增强。

1.2感受野

笔者看来，图片的感受野指的是图片的特定区域

当我们选定蓝框所在的区域时，我们仅仅提取框内的像素信息，对于图片的其他部分并没提取信息

此时，蓝框所在区域称为此时的感受野

人类识别物体是基于整体的思想而进行的

而机器更聚焦于图片的某个部分，也就是感受野所提供的信息

我们将感受野的灰度信息以一定的权重加以杂糅，这对人类来说十分抽象

但于机器而言就是对判断是否是某一物体的重要信息

二、卷积

2.1全连接网络

我们复习一下全连接网络（Fully Connected Neural Network）

全连接网络层与层之间神经元两两相连，每一连接则代表一个参数

其连接数为m*n，所以当神经元足够多时，参数量便十分的巨大

2.2一维卷积

一维卷积同全连接网络相似

神经元之间都是通过乘上参数进行连接

不过不同的是层与层之间的神经元选择性的连接，本层神经元只同上一层的部分神经元相连

图中神经元a只与x、y、z神经元相连，其只接受了x，y，z的有效信息

这里x，y，z便是感受野，其信息汇聚于神经元a

如此卷积网络的参数就大大减少了，并且本层的某一神经元只接受了上层部分神经元的信息

不过注意，本层神经元和上层神经元连接的数量是固定的，且有顺序的

在图中这种连接为为参数 $w=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ ，我们称之为滤波器（Filter）或者卷积核（Convolution Kernel），卷积核随着神经元计算而横向移动

抽象的，我们可以认为这是一个平移的过程，即连接随着神经元的平移而平移

2.3二维卷积

二维卷积同一维卷积类似，都是一个平移的过程

二维卷积常适用于图像数据，图像（或其他特征映射）经卷积产生的结果称为特征映射（feature map）

不过同的是，由于增加了一个维度，卷积核还要考虑纵向的移动

同时这里的卷积核由向量变为矩阵了，此时的连接为相应区域同卷积核相同部分相乘再相加

二维卷积运用的范围非常的广，在此介绍以下针对二维卷积的一些相关知识

首先，卷积核的平移未必只能是一个单位，还可能一次性移动多个单位，移动的单位数我们称之为步长（stride）

同时卷积核横向移动和纵向移动的步长不一定一致，二维卷积中我们用一个二维向量表示步长，例如 $stirde=(1,2)$ 便是横向移动时每次1个步长，而纵向移动时一次2个步长

当然，既然步长可以定义，卷积核的形状（kernel size）也可以定义，它不一定是长宽相等，形状为 $size=(2,1)$ 也未尝不可

为了使卷积后的特征图形状可以更好的控制，我们通过填充（padding）的方式

填充即在原特征图周围添加0

输入神经元个数经过不同大小卷积核、步长、填充得到不同大小的特征映射

输入神经元个数	$M$
卷积核大小	$K$
步长	$S$
填充	$P$

特征映射的大小为 $\frac{(M-K+2P))}{S}+1$

此公式对二维卷积同样适用

在步长为1的情况下，我们常用奇数大小的卷积核，如此我们可以设定填充数 $P=K-1$ ，使得特征映射同原图大小一致

同时，卷积网络还能满足对输入输出通道维数的控制

图中是一个由三维RGB图像向二维卷积的一个过程

输入是一个有着3通道的RGB图片，其分别和两个三通道的卷积核相乘再相加，于是得到了二维的卷积后的特征映射

不难看出，卷积网络中，卷积核的维度对应着输入维度大小（input size），而卷积核的数量对应着输出维度的大小（output size）

不同的卷积核具有不同的特征提取能力

下图便是一个很好的例子

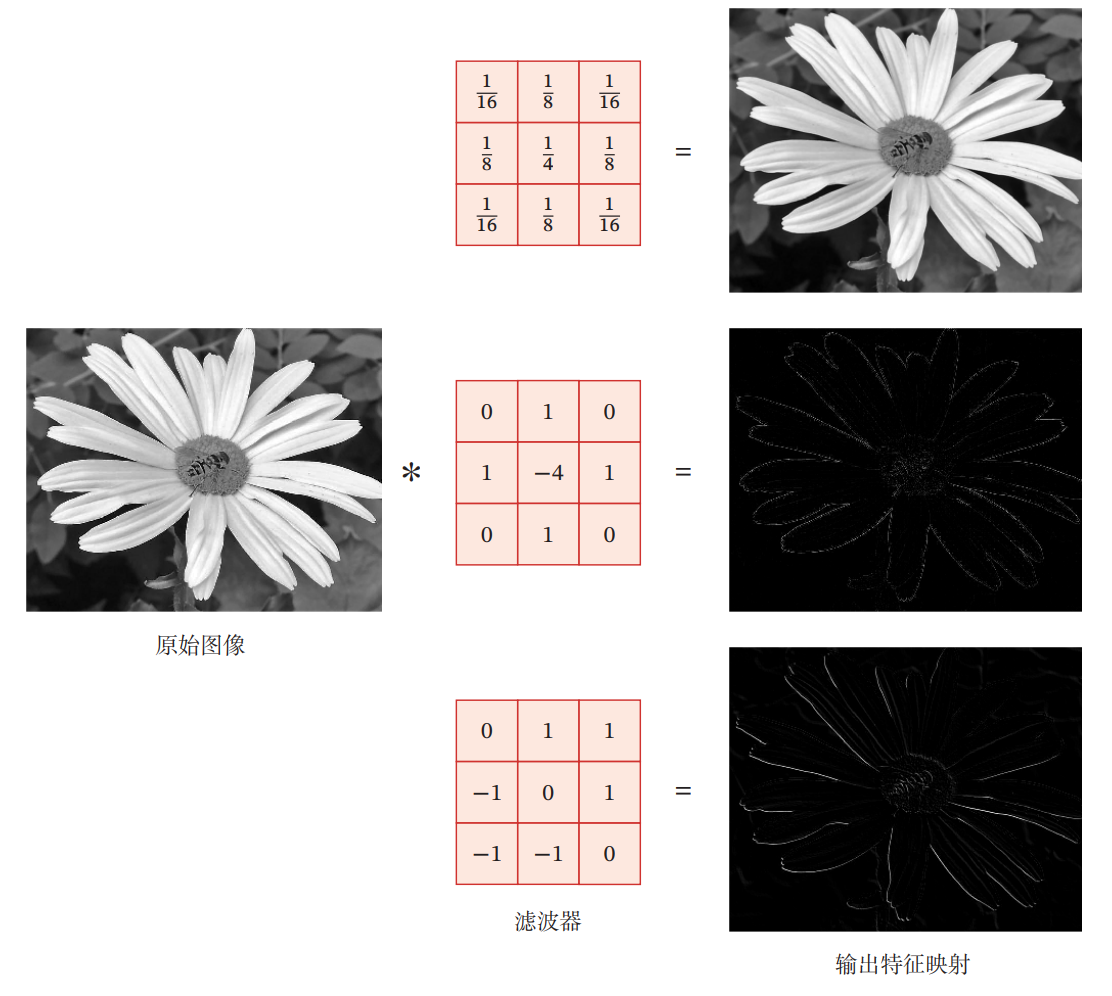
三、网络构成

3.1全连接与卷积

如果两层神经元之间采取的全连接模式，这就意味着任意两层的两个神经元之间都有一个权重参数

如果 $l$ 层有 $M_l$ 个神经元， $l-1$ 层有 $M_{l-1}$ 个神经元，那么就有 $M_l\times M_l-1$ 个权重参数

当每一层神经元数多，网络层数深的时候，参数的数量将会十分的爆炸

如果采用一维卷积来代替， $l$ 层的净输入 $z^{(l)}$ 为 $l-1$ 层激活值 $\alpha^{(l-1)}$ 与卷积核 $w^{(l)}\in R^K$ 的卷积输

出，用 $z^{(l)}=w^{(l)}\bigotimes \alpha^{(l-1)}+b^{(l)}$ 表示

其中 $\bigotimes$ 代表卷积操作； $w^{(l)}\in R^K$ 中的参数是可学习的， $b^{(l)}$ 作为偏置同样也是可以学习的

比起全连接网络而言，卷积的权重参数（也就是神经元之间的连接）少了很多

卷积有着局部连接和权重共享两条性质

1）局部连接

第 $l$ 层神经元只同 $l-1$ 层的部分神经元相连，连接数量同卷积核的大小一致

2）权重共享

也正是由于第 $l$ 层神经元是由 $l-1$ 层神经元经卷积操作变化而来，卷积过程即卷积核对 $l-1$ 层神经元进行滑动，所以不同的相邻的几组神经元他们是共享卷积核中的权值的（图中相同的颜色代表着相同的权值

3.2汇聚层

汇聚层可以理解为特殊的卷积层

汇聚（Pooling）是对特征映射进行下采样（Down sampling）操作，降低特征映射的大小，从而减小运算复杂度，避免过拟合

汇聚同卷积类似，都是有一窗口对数据进行滑动，提取窗口内的数据特征

常见的汇聚操作有平均汇聚以及最大汇聚

1）平均汇聚（Mean pooling）

即对窗口内所有数值取平均操作，可以理解为大小a*a的卷积核中，每一个参数均为 $\frac{1}{a^2}$

2）最大汇聚（Max pooling）

即对窗口内所有数值取最大操作，几乎认为这一操作是连续变换的，反向传播时也可以求导

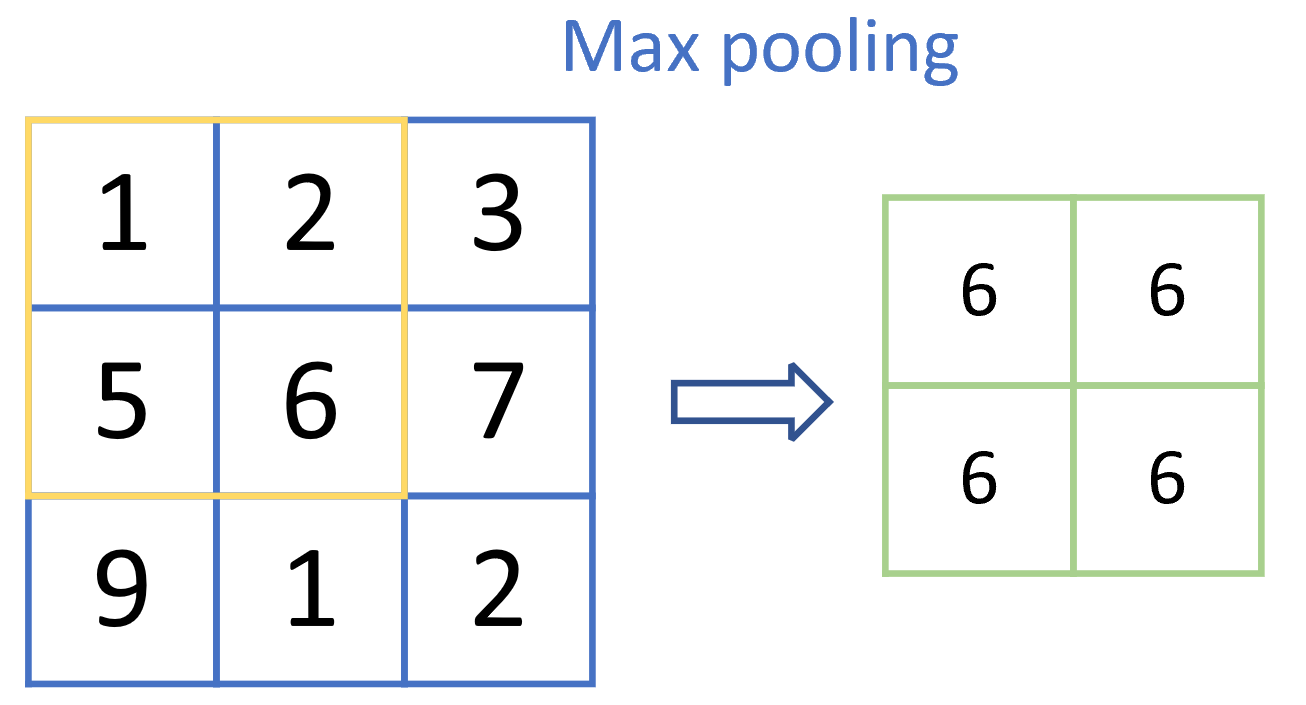
3.3卷积神经网络结构

一个典型的卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成

目前常用的卷积网络整体结构如下图所示所示

一个卷积块为连续 $M$ 个卷积层和 $b$ 个汇聚层（ $M$ 通常设置为2 ∼ 5， $b$ 为0或1）；一个卷积网络中可以堆叠 $N$ 个连续的卷积块，然后在后面接着 $K$ 个全连接层（ $N$ 的取值区间比较大，比如 1 ∼ 100或者更大； $K$ 一般为0 ∼ 2）

值得注意的是，在网络优化（3）提到的批量归一化，可以一定程度上防止梯度爆炸

在卷积神经网络中，我们往往把他看作一个等同卷积层、汇聚层这样的层来看待‘

笔者查阅了一些资料，关于卷积，激活以及BN的顺序

如果激活函数是ReLU函数，则顺序为Con-BN-ReLU

如果激活函数是Sigmoid函数，则顺序为Con-Sigmoid-BN