目录
一、凸优化
1.1评价标准
当我们建立模型之后,我们希望有一种标准来评价模型的好坏;
而优化问题的目的就是根据这一评价标准,使得我们向好的方向改正,这里的标准可以是最大化收益,亦可是最小化损失。
统计学习中,我们常用的是损失(Loss)来描述模型‘不好’的程度,损失越小,我们的模型就越好。
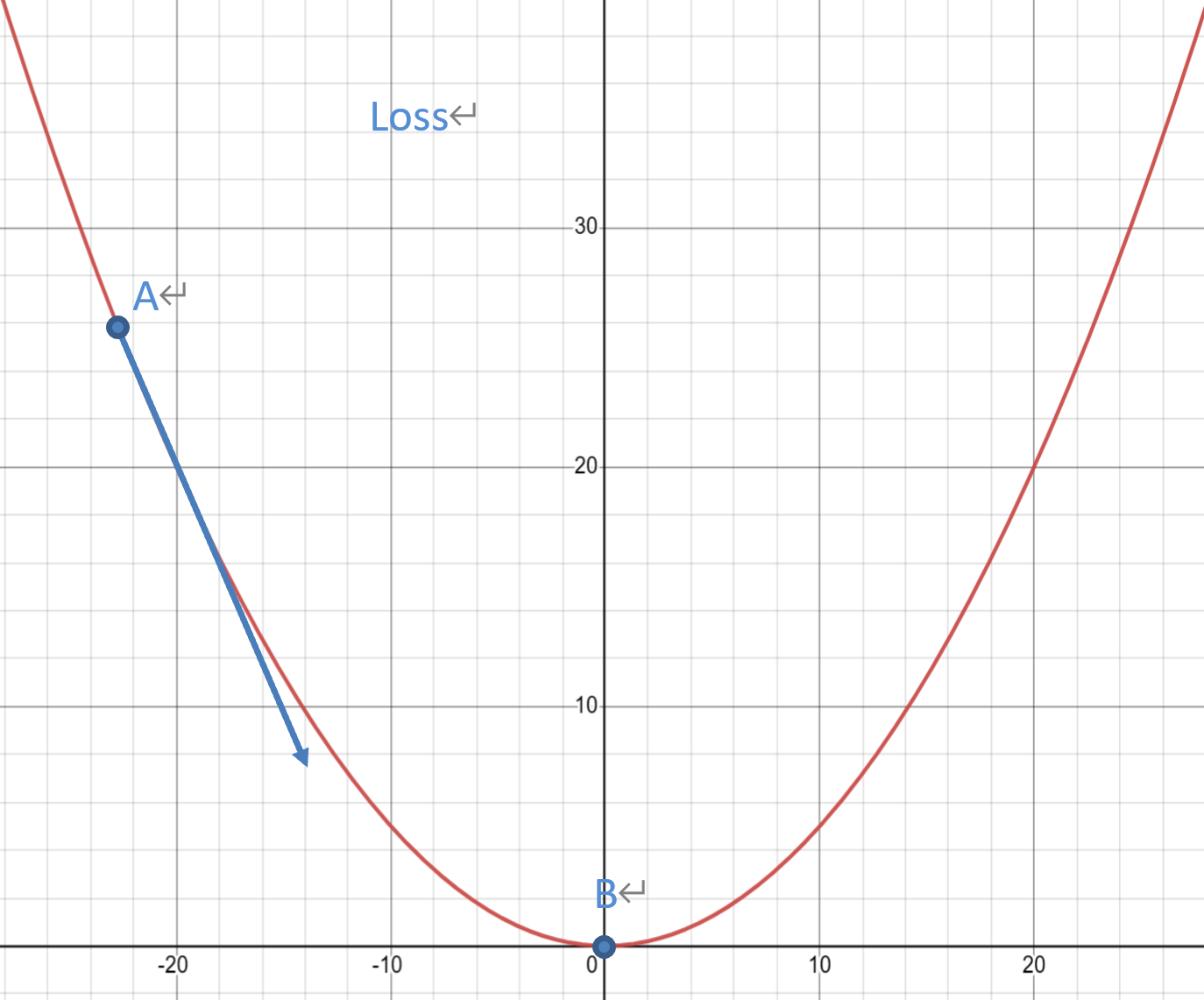
如果这个二次函数的图像是我们的损失图;
假设我们处于点A处,此时损失较大,我们期待它可以向箭头方向前进,以此达到损失减小的目的。当我们达到点B时,此时损失达到了函数最小值了,我们认为达成了我们的优化目的。
1.2驻点
不过现实是,我们优化模型的时候,找到损失最小点并不容易。
上图中损失最小点B点导数值为0,是驻点。
我们来看一下驻点的定义:驻点是导数值为0的点,的极值点一定是驻点或者导数不存在的点,然而反之却不一定。
我们来看一个例子,当我们构造形如的函数时,
处的导数为0,但0显然不是最大或者最小值点,甚至不是极值点。
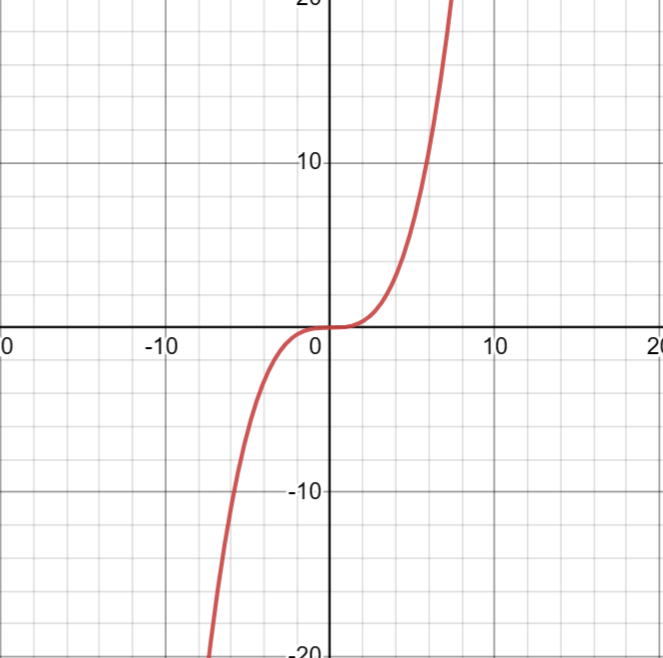
这给我们造成了许多困扰,我们只能通过导数值为0找到驻点,无法直接找到最值点;
当一个点时最值点时,他一定是驻点;但是驻点并不一定是最值点,他可能是局部极值点,或者鞍点。
那么我们是否可以通过一些条件的约束,使得我们的驻点就是我们的最值点呢?
1.3凸优化条件
满足以下条件的问题,我们定义为凸优化问题:
对于目标函数,限定为凸函数;对于优化变量的可行域,限定为凸集。
凸优化问题的解(就是损失的驻点)就是我们要找的最小值点
看一下凸集的定义:
如此定义的集合是凸集,可以理解为集合中任意两点的连线都在集合之内,集合的‘角’是向外凸出的,所以叫凸集。

再来看一下凸函数的定义:
如此定义为凸函数,可以理解为两点连线的值大于两点之间函数值
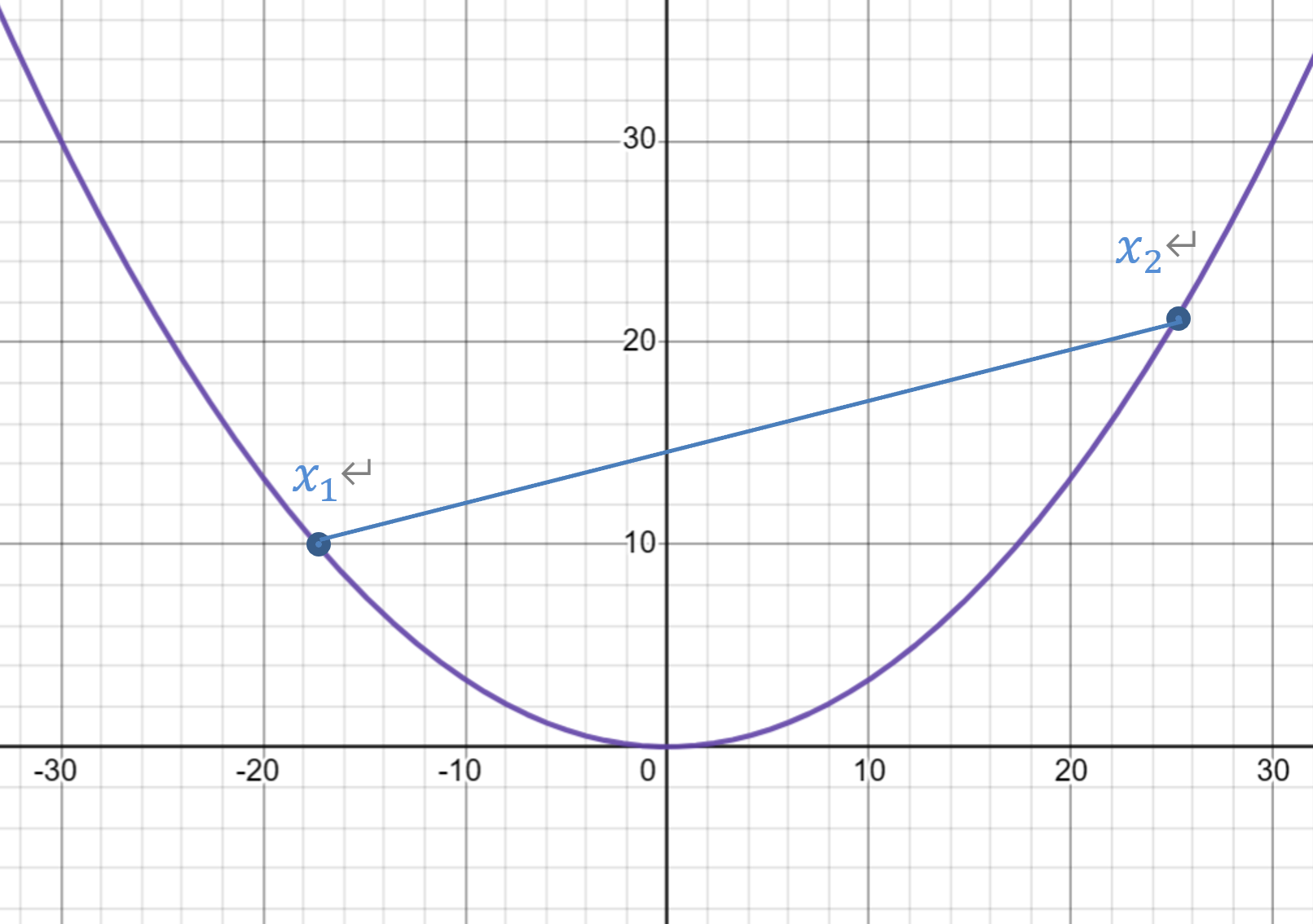
当定义域是凸集
是凸函数时,我们称为凸优化问题。
当定义域维数大于1时,我们列出其黑塞(Hessian)矩阵,如果黑塞矩阵半正定,则判断为凸函数。
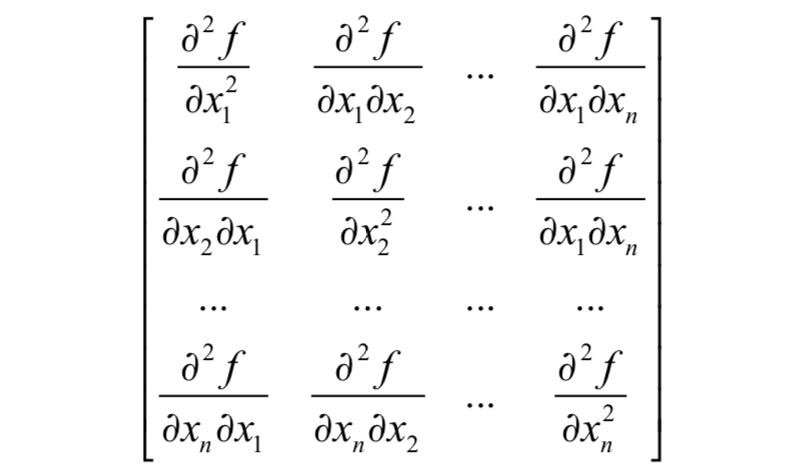
1.4凸优化形式
形如下式的优化问题称为凸优化问题;
其中为我们需要最小化的损失函数,
为不等式约束条件,
为等式约束条件。
二、梯度下降
2.1损失函数
损失函数是上述损失的数值化表达,用数字大小来衡量损失的强弱。
我们常用的损失有
1)均方损失(MSE)
其中是我们模型在我们输入某个样本特征后得到的预测值,而
是该样本的真实值,
是样本个数。
2)交叉熵损失(Cross Entropy)
交叉熵损失常用于衡量分类任务预测概率和真实标签的误差;当输入样本的特征之后,返回的是样本属于各类别的概率,且
;而样本的标签描述的是样本属于哪一类,如果属于第
类,那么样本的真实标签则为
,其中第
列为1其余全为0。
公式中,是预测概率,
是真实标签,
是类别个数,
是样本个数。
2.2梯度
设函数 在点
的某一邻域
内有定义,自点
引射线
,若
存在,则称
为点
沿
方向的方向导数。
显然我们可以找到无数条射线,这也代表着方向导数有无限多,而我们关注的是其中最大的一个,其含义为:沿着该方向函数变化的最快;这就是我们说的梯度。
损失函数的梯度是我们重点关注的对象,损失的最小负梯度方向是减小最快的方向,我们该方向优化可以使我们的损失更快的降低。
我们来看一个实例:
当我们想拟合直线时,我们寻找直线上两个点
以及
,我们对这两点的预测值为
,对应关系为
,其中
为初始参数;
此时我们拥有我们的预测值以及真实值
,我们便可以计算我们的预测损失;这里使用MSE损失,于是损失:
我们用损失分别对求导得到:
是我们待优化的参数,我们希望通过改变他们从而降低损失;
其中是步长,常取0.01,其含义为参数一次更新迈的‘步子’大小。
我们如此进行一次,就代表我们参数完成了一次更新;其含义为:我们朝着损失减小最快的方向更新。





















 833
833











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








