永磁同步电机学习日志总结Day6-1

关于调制比m的定义，在不同的论文里面有不同的表述，所以最终一区二区分界的m值也会不同。但是经过计算，比例是一样的，一个重大发现。

主流的有以下几种：

线性调制区：0<m<1，过调制区：1<m<1.103，m=sqrt(3)*Um/Udc。（传统调制度定义）

线性调制区：0<m<0.9069，过调制区：0.9069<m<1，m=pi/2*Um/Udc。（过调制调制度定义）

线性调制区：0<m<0.866，过调制一区：0.866<m<0.909，过调制二区：0.909<m<1，m=3/2*Um/Udc。

线性调制区：1<m<1.049，过调制一区：1.049<m<1.154，过调制二区：1.154<m，（最终要用的m定义）

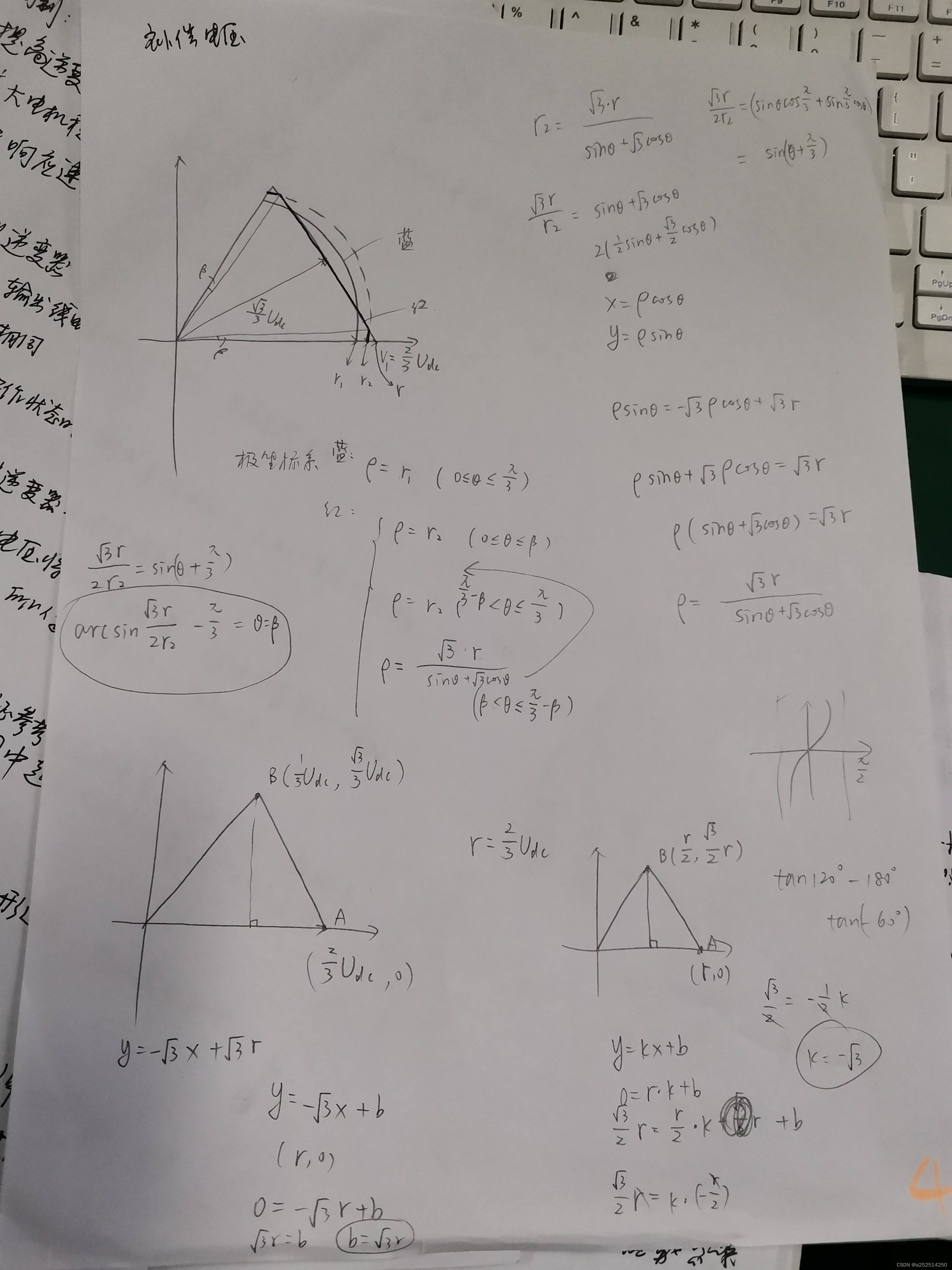
以上是对于参考电压和实际电压的坐标转换，使用到的数学知识是极坐标和三角函数变换（高中数学选修以及必修四）（感谢lxy的帮助）

最终得出的结果与某篇论文相互印证是正确的。（验证在“6”里）

 

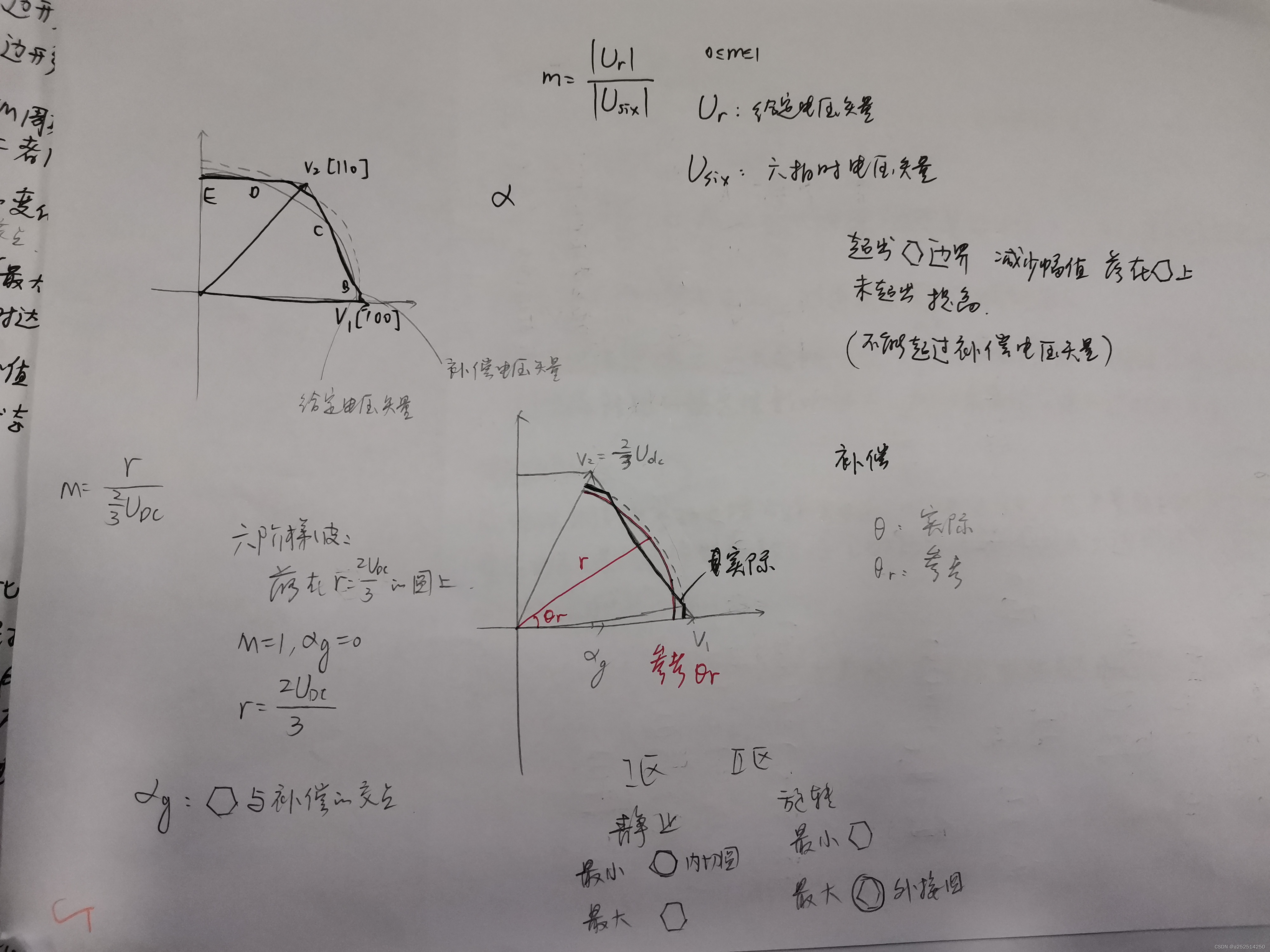
参考电压模长为r。V1模长为2/3*Udc。内切圆半径为Udc/sqrt(3)。

线性调制：0<r<Udc/sqrt(3)，即内切圆内部。

过调制一区：Udc/sqrt(3)<r<六边形边界。

过调制二区：六边形边界<r<2/3*Udc，即六边形外接圆。

线性调制区不多赘述。

过调制一区：补偿电压矢量是圆弧，半径大于参考电压模长，但是小于V1。

过调制二区：补偿电压矢量半径最大就是V1了，不能再大了，此时实际电压落在六边形边界上。如果要再增大，需要借用V1的长度，相当于旋转起来。但是由于开始就进行两次坐标变换，此时只需返璞归真就行，所以实际操作是让V1停留时间长一些即可。

由此总结，过调制一区的参考电压矢量和实际电压矢量角度是一样的，但是模长会不一样；过调制二区为了得到长时间停留的V1，角度会跳变。过调制二区最终得到的是六阶梯波。

 

 

 

 对我很有帮助的是这篇论文：

 文章比较完备地叙述了线性调制区、过调制一区、过调制二区的定义和算法。