Codeforces 815A-Karen and Game

Karen and Game

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.

One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.

To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.

Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!

Input

The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.

The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).

Output

If there is an error and it is actually not possible to beat the level, output a single integer -1.

Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.

The next k lines should each contain one of the following, describing the moves in the order they must be done:

• row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
• col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".

If there are multiple optimal solutions, output any one of them.

Examples

input

3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1

output

4
row 1
row 1
col 4
row 3

input

3 3
0 0 0
0 1 0
0 0 0

output

-1

input

3 3
1 1 1
1 1 1
1 1 1

output

3
row 1
row 2
row 3

Note

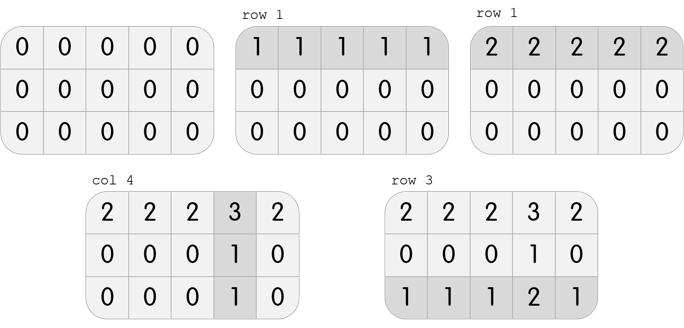
In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:

In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.

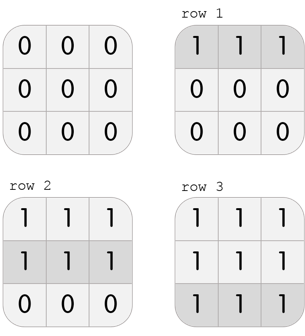
In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:

Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.

题意：给你一个初始全为零的n*m的方格，每次操作可以使一行或一列全部加一，问最少要操作几步能使方格和输入一样

解题思路：可以将输入给的方格全部清为零，那么只要每次将一行或一列不含零的全部减去这一行或这一列的最小值，因为步数要最少，所以行和列那个少先找哪个

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <set>
#include <stack>
#include <map>
#include <climits>

using namespace std;

#define LL long long
const int INF = 0x3f3f3f3f;

int n, m;
int a[200][200], ans[300], vis[2][300], cnt[300];
string s[300];

int main()
{
	while (~scanf("%d%d", &n, &m))
	{
		int sum = 0, step = 0, res = 0;
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
			{
				scanf("%d", &a[i][j]);
				if (a[i][j]) sum++;
			}
		memset(vis, 0, sizeof vis);
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= m; j++)
				if (!a[i][j]) { vis[0][i] = 1; break; }
		}
		for (int i = 1; i <= m; i++)
		{
			for (int j = 1; j <= n; j++)
				if (!a[j][i]) { vis[1][i] = 1; break; }
		}
		while (1)
		{
			int flag = 0;
			for (int k = n < m ? 0 : 1, p = 0; p < 2; p++, k = (k + 1) % 2)
			{
				for (int i = 1; i <= (!k ? n : m); i++)
				{
					if (!vis[k][i])
					{
						int mi = INF;
						if (!k)
						{
							for (int j = 1; j <= m; j++)
								mi = min(mi, a[i][j]);
						}
						else
						{
							for (int j = 1; j <= n; j++)
								mi = min(mi, a[j][i]);
						}
						if (!mi) { vis[k][i] = 1; continue; }
						flag = 1;
						if (!k)
						{
							for (int j = 1; j <= m; j++)
							{
								a[i][j] -= mi;
								if (!a[i][j]) sum--;
							}
						}
						else
						{
							for (int j = 1; j <= n; j++)
							{
								a[j][i] -= mi;
								if (!a[j][i]) sum--;
							}
						}
						if(!k) s[step] = "row";
						else s[step] = "col";
						ans[step] = i;
						cnt[step++] = mi;
						res += mi;
						vis[k][i] = 1;
					}
				}
			}
			if (!flag) break;
		}
		if (sum) printf("-1\n");
		else
		{
			printf("%d\n", res);
			for (int i = 0; i < step; i++)
				for (int j = 1; j <= cnt[i]; j++)
					cout << s[i] << " " << ans[i] << endl;
		}
	}
	return 0;
}