【数值分析】数值积分——Newton—Cotes求积公式、龙贝格求积法

将区间 $[a,b]$ 分为n段区间，即 $a=x_{0}<x_{1}<x_{2}<\cdots <x_{n}=b$ ，每个子区间的长度 $\Delta x_{i}=(x_{i}-x_{i-1}),(i=1,2,\cdots ,n)$ 在每个子区间上任取一点 $\xi _{i}\in [x_{i},x_{i-1}],(i=1,2,\cdots n)$ ，当区间足够小时，每个区间的面积可近似为 $\Delta S_{i}=f(\xi _{I})\Delta x_{i}$ ，对 $\Delta S_{i}$ 求和 $S=\sum_{i=1}^{n}\Delta S_{i}=\sum_{i=1}^{n}f(\xi _{i})\Delta x_{i}$

对 $\Delta x_{i}$ 去极限，则曲边梯形的面积 $A=\lim_{\Delta x_{i}\rightarrow 0}S=\lim_{\Delta x_{i}\rightarrow 0}\sum_{i=1}^{n}f(\xi _{i})\Delta x_{i}$

牛顿—莱布尼兹公式： $\int_{a}^{b}f(x)dx=F(b)-F(a)$ ，该公式在求解含函数 $f(x)$ 的定积分时，若函数 $f(x)$ 的原函数 $F(x)$ 容易得到，那么可以得到一个精确解。但在实际问题中很多函数 $f(x)$ 的原函数难以求解或无法找到，导致无法使用牛顿—莱布尼兹公式。

数值积分面临的问题： $f(x)$ 的表达式未知； $f(x)$ 的原函数不能初等表示，如何求解 $\int_{a}^{b}f(x)dx$ 的可估计误差的近似值？

只利用有限节点和函数在有限个节点处的函数值计算积分，只涉及加减乘除四则运算。

对积分得近似求解有以下方法：

矩形法： $\int_{a}^{b}f(x)dx=\sum_{k=1}^{n}\int_{x_{k-1}}^{x_{k}}f(x)dx\approx \sum_{k=1}^{n}(x_{k}-x_{k-1})f(x_{k})$

梯形法： $\int_{a}^{b}f(x)dx\approx \sum_{k=1}^{n}\frac{1}{2}(x_{k}-x_{k-1})[f(x_{k-1})+f(x_{k})]$

数值积分公式

·数值积分公式的一般形式

$\int_{a}^{b}f(x)dx\approx \sum_{k=0}^{n}A_{k}f(x_{k})$ 式中 $x_{k}$ 称为求积节点， $A_{k}$ 称为求积系数， $A_{k}$ 仅与节点 $x_{k}$ 的选取有关， $A_{k}$ 不依赖于被积函数 $f(x)$ 的具体形式。

设给定一组节点 $a\leq x_{0}<x_{1}<x_{2}<\cdots <x_{n}\leq b$ ，以多给的n+1个节点作插值节点作函数 $f(x)$ 的插值多项式： $L_{n}(x)=\sum_{k=0}^{n}l_{k}f(x_{k})$ ，带入求积公式： $\int_{a}^{b}f(x)dx\approx \int_{a}^{b}L_{n}(x)dx=\sum_{k=0}^{n}\int_{a}^{b}l_{k}(x)dxf(x_{k})$ ， $A_{k}=\int_{a}^{b}l_{k}(x)dx$

$l_{k}=\prod_{j=0,j\neq k}^{n}\frac{x-x_{j}}{x_{k}-x_{j}},$ $R_{n}(f)=\int_{a}^{b}f(x)dx-\int_{a}^{b}L_{n}(x)dx=\int_{a}^{b}\frac{f^{(n+1)}(\xi )}{(n+1)!}\omega _{(n+1)}(x)dx$

但在上述公式中插值型求积公式的求积系数当节点不等距很难求得，误差表达式中得不确定点的处理有难度。

·Newton—Cotes求积公式

设将积分区间 $[a,b]$ n等分，记步长 $h=\frac{b-a}{n}$ ，选取等距节点 $x_{k}=a+kh$

将 $x_{k}=a+kh,h=\frac{b-1}{n},x=a+th$ 代入求积公式得： $\int_{a}^{b}f(x)dx\approx \int_{a}^{b}L_{n}(x)dx=\sum_{k=0}^{n}\int_{a}^{b}l_{k}(x)dxf(x_{k})$

$A_{k}=\int_{a}^{b}\prod_{0\leq j\leq n,j\neq k}\frac{x-x_{j}}{x_{k}-x_{j}}dx=\int_{0}^{n}(\prod_{0\leq j\leq n,j\neq k}\frac{(t-j)h}{(k-j)h})hdt=$ $\frac{(-1)^{n-k}h}{k!(n-k)!)}\int_{0}^{n}\prod_{0\leq j\leq n,j\neq k}(t-j)dt$

$A_{k}=(b-a)\frac{(-1)^{n-k}}{nk!(n-k)!}\int_{0}^{n}\prod_{0\leq j\leq n}^{j\neq k}(t-j)dt=C_{k}^{(n)}(b-a)$

Newton—Cotes求积公式可改写为： $Q[f]=\sum_{k=0}^{n}A_{k}f(x_{k})=\sum_{k=0}^{n}C_{k}^{(n)}(b-a)f(x_{k})=$ $(b-a)\sum_{k=0}^{n}C_{k}^{(n)}f(x_{k})$

其中： $C_{k}^{(n)}=\frac{(-1)^{n-k}}{nk!(n-k)!}\int_{0}^{n}\prod_{0\leq j\leq n}^{j\neq k}(t-j)dt,C_{k}^{(0)}=C_{n-1}^{n},\sum_{k=0}^{n}C_{k}^{(0)}=1$ （插值型、节点等距）

·梯形求积公式（n=1）

取 $n=1$ ， $x_{0}=a,x_{1}=b,h=b-a$

Cotes系数为： $C_{0}^{(1)}=-\int_{0}^{1}(t-1)dt=\frac{1}{2},C_{1}^{(1)}=\int_{0}^{1}tdt=\frac{1}{2}$

求积公式为： $Q[f]=(b-a)\sum_{k=0}^{1}C_{k}^{(1)}f(x_{k})=\frac{b-a}{2}[f(x_{0})+f(x_{1})]$

即， $I[f]\approx Q[f]=\frac{b-a}{2}[f(a)+f(b)]$ 称为梯形求积公式

$R_{1}(f)=\int_{a}^{b}f(x)dx-\int_{a}^{b}L_{1}(x)dx=\int_{a}^{b}\frac{f^{2}(\xi )}{2!}\omega_{2}(x)dx$ $=\int_{a}^{b}\frac{f^{2}(\xi )}{2!}(x-a)(x-b)dx=\frac{f_{''(\xi )}}{2}[\frac{x^{3}}{3}-(a+b)\frac{x^{2}}{2}+abx]_{a}^{b}$

$=-\frac{f^{''}(\eta )}{12}(b-a)^{3}$

·辛普森求积公式（n=2）

取 $n=2,x_{0}=a,x_{1}=\frac{b+a}{2},x_{2}=b,h=\frac{b-a}{2}$

Cotes系数为： $C_{0}^{(2)}=\frac{-1}{2}\int_{0}^{2}(t-1)(t-2)dt=\frac{1}{6},C_{1}^{(2)}=\frac{-1}{2}\int_{0}^{2}t(t-2)dt=\frac{4}{6}$ $,C_{2}^{(2)}=\frac{1}{4}\int_{0}^{2}t(t-1)dt=\frac{1}{6}$

求积公式为： $Q[f]=(b-a)\sum_{k=0}^{2}C_{k}^{(2)}f(x_{k})=(b-a)[\frac{1}{6}f(x_{0})+\frac{4}{6}f(x_{1})+\frac{1}{6}f(x_{2})]=$ $\frac{b-a}{6}[f(a)+4f(\frac{a+b}{2})+f(b)]$

即， $I[f]\approx Q[f]=\frac{b-a}{6}[f(a)+4f(\frac{a+b}{2})+f(b)]=\frac{h}{3}[f(a)+4f(\frac{a+b}{2})+f(b)]$

取 $H_{3}(a)=f(a),H_{3}(b)=f(b),H_{3}(\frac{a+b}{2})=f(\frac{a+b}{2}),H^{'}_{3}(\frac{a+b}{2})=f^{'}(\frac{a+b}{2})$

根据Hermite插值余项：

$R(x)=f(x)-H_{3}(x)=\frac{f^{4}(\xi )}{4!}(x-a)(x-\frac{a+b}{2})^{2}(x-b)$

$\int_{a}^{b}R(x)dx=\frac{1}{4!}\int_{a}^{b}f^{(4)}(\xi )(x-a)(x-\frac{a+b}{2})^{2}(x-b)dx$

由积分中值定理知： $\eta \in (a,b),R(f)=\frac{f^{4}(\eta )}{4!}\int_{a}^{b}(x-a)(x-\frac{a+b}{2})^{2}(x-b)dx=-\frac{(b-a)^{5}}{2880}f^{(4)}(\eta )$

·代数精度

分析插值型求积公式得余项： $R(f)=\int_{a}^{b}[f(x)-p(x)]dx=\int_{a}^{b}\frac{f^{(n+1)}(\xi )}{(n+1)!}\omega (x)dx$

当f(x)是次数不高于m的多项式时，有 $f^{(n+1)}(x)=0,R(f)=0$ 求积公式能成为准确的等式。闭区间 $[a,b]$ 上的连续函数可用多项式逼近。

对于一个一般的求积公式： $\int_{a}^{b}f(x)dx\approx \sum_{k=0}^{n}A_{k}f(x_{k})$ 如果对于次数不超过m的多项式均能准确的成立，但对于m+1次多项式不准确成立，则称该求积公式具有m次代数精度。

证明方法：对于当 $f(x)$ 分别为 $\begin{Bmatrix} 1,x,x^{2},\cdots ,x^{m} \end{Bmatrix}$ 时，求积公式 $\int_{a}^{b}f(x)dx\approx \sum_{k=0}^{n}A_{k}f(x_{k})$ 精确成立。当 $f(x)=x^{m+1}$ 时， $\int_{a}^{b}f(x)dx\approx \sum_{k=0}^{n}A_{k}f(x_{k})$ 不精确成立即可。

一般地要是求积公式具有m次精度，只要令 $f(x)=1,x,\cdots ,x^{m}$ 都能准确成立，这就要求

$\left\{\begin{matrix} \sum_{k=0}^{n}A_{k}=b-a=\int_{a}^{b}1dx\\ \sum_{k=0}^{n}A_{k}x_{k}=\frac{1}{2}(b^{2}-a^{2})=\int_{a}^{b}xdx\\ \cdots \\ \sum_{k=0}^{n}A_{k}x_{k}^{m}=\frac{1}{m+1}(b^{m+1}-a^{m+1})=\int_{a}^{b}x^{m}dx \end{matrix}\right.$ ，构造求积公式原则上是确定参数 $x_{k}$ 和 $A_{k}$ 的代数问题。

定理：n+1个节点的求积公式 $\int_{a}^{b}f(x)dx\approx \sum_{k=0}^{n}A_{k}f(x_{k})$ 为插值型求积公式的充分必要条件是公式至少具有n次代数精度。

证明：

必要性：n+1个节点的插值型求积公式的求积系数及余项为：

$A_{k}=\int_{a}^{b}l_{k}(x)dx,R_{n}(x)=\int_{a}^{b}\frac{f^{n+1}(\xi )}{(n+1)!}\omega _{n+1}(x)dx$ ，而 $\int_{a}^{b}f(x)dx=\int_{a}^{b}P(x)dx+\int_{a}^{b}R(x)dx$

当 $f(x)$ 为不高于n次的多项式时，余项 $R(x)=0$ ，所以求积公式至少具有m次代数精度。

充分性：若求积公式至少有n次代数精度，则对n次多项式 $l_{k}(x)=\prod_{j=0,j\neq k}^{n}\frac{x-x_{j}}{x_{k}-x_{j}},k=0,1,\cdots ,n$ 精确成立，即 $\int_{a}^{b}l_{k}(x)dx=\sum_{j=0}^{n}A_{k}l_{k}(x_{k})$ ，而 $l_{k}(x_{j})=\delta _{kj}=\left\{\begin{matrix} 1,k=j\\ 0,k\neq j \end{matrix}\right.$ ，

取 $f(x)=l_{k}(x),\int_{a}^{b}f(x)dx=\int_{a}^{b}l_{k}(x)dx=\sum_{j=0}^{n}A_{j}l_{k}(x_{j})=A_{k}$ ，所以有 $\int_{a}^{b}l_{k}(x)dx=A_{k}$ ，即求积公式为插值型求积公式。

定理：当n为偶数时，牛顿—科特斯求积公式至少具有n+1次代数精度。

·复化求积

Newton—Cotes求积公式在节点较多时，由于高次插值的不稳定导致不稳定。复化求积法将区间分为若干个子区间，在每个子区间上用低阶求积公式。

·复化梯形公式

将区间 $[a,b]$ 分为n等分，分点 $x_{i}=a+kh,h=\frac{b-a}{n},k=0,1,\cdots ,n$ ，在每个子区间 $[x_{k},x_{k+1}](k=0,1,\cdots ,n-1)$ 上引用梯形公式 $\int_{x_{k}}^{x_{k+1}}f(x)dx=\frac{h}{2}[f(x_{k}+f(x_{k+1})]-\frac{h^{3}}{12}f^{''}(\eta _{k}),\eta _{k}\in [x_{k},x_{k+1}]$ ，求和可得：

$I=\int_{a}^{b}f(x)dx=\sum_{k=0}^{n-1}\int_{x_{k}}^{x_{k+1}}f(x)dx=\frac{h}{2}\sum_{k=0}^{n-1}[f(x_{k}+f(x_{k+1})]$ $+R_{n}(f)$

$T_{n}=\frac{h}{2}[f(x_{0})+\sum_{k=1}^{n-1}f(x_{k})+\sum _{k+0}^{n-2}f(x_{k+1})+f(x_{n})]$ $=\frac{h}{2}[f(a)+2\sum_{k=1}^{n-1}f(x_{k})+f(b)]$

$R_{T}(f)=\int_{a}^{b}f(x)dx-T_{n}=-\frac{h^{3}}{12}\sum_{k=0}^{n-1}f^{''}(\xi _{k})$ ， $f^{''}(x)$ 在 $[a,b]$ 连续，故 $\eta \in [a,b]$ ，使得 $f^{''}(\eta )=\frac{1}{n}\sum_{k=0}^{n-1}f^{''}(\xi _{k})$

$\therefore R_{T}(f)=\int_{a}^{b}f(x)dx-T_{n}=-\frac{h^{3}}{12}nf^{''}(\eta )=-\frac{b-a}{12}h^{2}f^{''}(\eta )$

$f(x)\in C^{2}[a,b]$ 时可以证明： $lim_{n\rightarrow \propto }T_{n}=\int_{a}^{b}f(x)dx$

·复化辛普森公式

将区间 $[a,b]$ 分为n=2m等分，分点 $x_{k}=a+kh,h=\frac{b-a}{n},k=0,1,\cdots ,n$ ，在每个子区间 $[x_{2k-2},x_{2k}]$ 上引用，辛普森公式得：

$S(x)=\int_{x_{2k-2}}^{2k}f(x)dx\approx \frac{x_{2k}-x_{2k-2}}{6}[f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})]$ $=\frac{h}{3}[f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})]$

$S_{n}=\frac{h}{3}\sum_{k=1}^{m}[f(x_{2k-2})+4f(x_{2k-1})+f(x_{2k})]$ $=\frac{h}{3}[f(a)+4\sum_{k=1}^{m}f(x_{2k-1})+2\sum_{k=1}^{m-1}f(x_{2k})+f(b)]$

$R_{S}(f)=\int_{a}^{b}f(x)dx-S_{n}=-\frac{(2h)^{5}}{2880}\sum_{k=1}^{m}f^{(4)}(\xi _{k}),\xi _{k}\in [x_{2k-2},x_{2k}]$

$f^{(4)}(x)$ 在区间[a,b]连续，故 $\eta \in [a,b]$ ，使得 $f^{''}(\eta )=\frac{1}{m}\sum_{k=0}^{n-1}f^{(4)}(\xi _{k})$

$\therefore R_{s}(f)=\int_{a}^{b}f(x)dx-S_{n}=-\frac{(2h)^{5}}{2880}mf^{4}(\eta )=-\frac{b-a}{180}h^{4}f^{(4)}(\eta )$ ， $\eta \in (a,b)$

$f(x)\in C^{2}[a,b]$ 时可以证明： $lim_{m\rightarrow \propto }S_{n}=\int_{a}^{b}f(x)dx$

·逐次分半算法

·梯形法的逐次分半算法

设将区间[a,b]分为n等分，共有n+1个分电，如果将求积区间再二分一次，则分点增加至2n+1个

每个子区间 $[x_{k},x_{k+1}]$ 经过二分增加了一个分点， $x_{k+\frac{1}{2}}=\frac{1}{2}(x_{k}+x_{k+1})$ ，用复化梯形求积公式求得该子区间上的积分值为： $\int_{x_{k}}^{x_{k+1}}=\frac{1}{2}\frac{h}{2}[f(x_{k})+2f(x_{k+\frac{1}{2}})+f(x_{k})]$ ， $T_{2n}=\frac{h}{4}\sum_{k=0}^{n-1}[f(x_{k})+f(x_{k+1})]+2\frac{h}{4}\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$ ,

复化梯形公式： $T_{n}=\frac{h}{2}[f(a)+2\sum_{k=1}^{n-1}f(x_{k})+f(b)]$ ，得出梯形法的逐次分半公式： $T_{2n}=\frac{1}{2}T_{n}+\frac{h}{2}\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$

·逐次分半算法：

梯形公式： $T_{1}=\frac{b-a}{2}[f(a)+f(b)]$

将区间[a,b]二等分，每个小区间的长度为 $\frac{b-a}{2}$ ， $T_{2}=\frac{T_{1}}{2}+\frac{h}{2}f(a+\frac{h}{2})$ ；

将区间[a,b]四 $(2^{2})$ 等分，每个小区间的长度为 $\frac{b-a}{2^{2}}=\frac{b-a}{4}$ ， $T_{4}=\frac{T_{2}}{2}+\frac{h}{2^{2}}[f(a+\frac{h}{4})+f(a+\frac{3h}{4})]$ ；

……

将区间[a,b] $2^{k}$ 等分，分点 $x_{i}=a+\frac{b-1}{2^{k}}i(i=0,1,2,\cdots ,2^{k})$ ，每个小区间的长度为 $\frac{b-a}{2^{k}}$ ，由归纳法可得：

$T_{2^{k}}=\frac{1}{2}T_{2^{k-1}}+\frac{b-a}{2^{k}}\sum_{i=1}^{2^{k-1}}f[]a+\frac{b-a}{2^{k}}(2i-1)]$

·龙贝格求积法

复化梯形公式算法简单，但收敛慢，精度低，由复化梯形求积公式的余项表达式知：

$\because I-T_{N}=-\frac{b-a}{12}h^{2}f^{''}(\eta ),\eta \in (a,b);I-T_{2n}=-\frac{b-a}{12}(\frac{h}{2})^{2}f^{''}(\overline{\eta} ),$ $\overline{\eta} \in (a,b)$

假定， $f^{''}(\eta )\approx f^{''}(\overline{\eta })\Rightarrow \frac{I-T_{2n}}{I-T_{n}}\approx \frac{1}{4}\Rightarrow I-T\approx \frac{1}{3}(T_{2n}-T_{n})$ ，若 $T_{2n}-T_{n}$ 很小，可保证 $T_{2n}$ 的误差很小

$I\approx T_{2n}+\frac{1}{3}(T_{2n}-T_{n})=\frac{4}{3}T_{2n}-\frac{1}{3}T_{n}=\frac{4T_{2n}-T_{n}}{4-1}$

当n=1时，我们计算上式右端：

$T=\frac{4t_{1}-t_{1}}{4-1}=\frac{4}{3}\frac{b-a}{2}[\frac{1}{2}f(a)+f(\frac{a+b}{2})+\frac{1}{2}f(b)]-\frac{1}{3}(b-a)[\frac{1}{2}f(a)+\frac{1}{2}f(b)]$

$=(b-a)[\frac{1}{6}f(a)+\frac{4}{6}f(\frac{a+b}{2})+\frac{1}{6}f(b)]=S_{1}$

这恰好是辛普森公式的结果，即有 $S_{1}=\frac{4}{4-1}T_{2}-\frac{1}{4-1}T_{1}$

类似的可验证： $S_{2}=\frac{4}{4-1}T_{4}-\frac{1}{4-1}T_{2},\cdots, S_{n}=\frac{4}{4-1}T_{2n}-\frac{1}{4-1}T_{n}$

即： $S_{n}=\frac{4}{3}T_{2n}-\frac{1}{3}T_{n}$

复化辛普森求积公式的余项：

$R_{n}=I-S_{n}=-\frac{b-a}{180}(\frac{h}{2})^{4}f^{(4)}(\eta )=O(h^{4}),$ $R_{2n}=I-S_{2n}=-\frac{b-a}{180}(\frac{h}{4})^{2}f^{(4)}(\overline{\eta })$

假定， $f^{(4)}(\eta )\approx f^{(4)}(\overline{\eta })\Rightarrow \frac{I-S_{2n}}{I-S_{n}}\approx \frac{1}{16}\Rightarrow I-S\approx \frac{1}{15}(S_{2n}-S_{n})$ ， $I\approx S_{2n}+\frac{1}{15}(S_{2n}-S_{n})\approx \frac{4^{2}S_{2n}-S_{n}}{4^{2}-1}$

可验证： $C_{n}=\frac{16}{15}S_{2n}-\frac{1}{15}S_{n},C_{n}$ ——复化柯特斯积分值

事实上， $C_{1}=\frac{4^{2}S_{2}-S_{1}}{4^{2}-1}=\frac{16}{15}S_{2}-\frac{1}{15}S_{1}=\frac{7y_{0}+32y_{1}+12y_{2}+32y_{3}+7y_{4}}{90}$ 恰为柯斯特公式

同理： $C_{2}=\frac{4^{2}S_{4}-S_{2}}{4^{2}-1}$

根据柯斯特积分公式的余项： $R_{n}=I-C_{n}=-\frac{2(b-a)}{945}(\frac{h}{4})^{6}f^{(6)}(\eta ),$ $R_{2n}=I-C_{2n}=-\frac{2(b-a)}{945}(\frac{h}{8})^{6}f^{(6)}(\overline{\eta })$

$\frac{I-C_{2n}}{I-C_{n}}\approx \frac{1}{64},I\approx \frac{64}{63}C_{2n}-\frac{1}{63}C_{n}$ ， $R_{n}=\frac{4^{3}C_{2n}-C_{n}}{4^{3}-1},R_{n}$ ——龙贝格积分值

即， $R_{1}=\frac{4^{3}C_{2}-C_{1}}{4^{3}-1},R_{2}=\frac{4^{3}C_{4}-C_{2}}{4^{3}-1},\cdots ,R_{n}=\frac{4^{3}C_{2n}-C_{n}}{4^{3}-1}$ ，该式为龙贝格公式得到的龙贝格序列

用若干个积分近似值推算出更为精确的积分近似值的方法，成为外推方法。

序列 $\begin{Bmatrix} T_{N} \end{Bmatrix},\begin{Bmatrix} S_{N} \end{Bmatrix},\begin{Bmatrix} C_{N} \end{Bmatrix},\begin{Bmatrix} R_{N} \end{Bmatrix}$ 分别成为梯形序列、辛普森序列、科特斯序列和龙贝格序列。由龙贝格序列还可以继续外推，但因 $\frac{4^{m}}{4^{m}-1}\approx 1$ 及 $\frac{1}{4^{m}-1}\approx 0(m\geq 4),$ 故通常到龙贝格序列为止。

记 $T_{m}^{k}=\frac{4^{m}T_{m-1}^{k+1}-T_{m-1}^{(k)}}{4^{m}-1},(m=1,2,\cdots ,k=0,1,2,\cdots )$

则 $\begin{Bmatrix} T_{0}^{k} \end{Bmatrix}$ 就是梯形值序列 $\begin{Bmatrix} T_{2} \end{Bmatrix}$ ， $\begin{Bmatrix} T_{1}^{k} \end{Bmatrix}$ 就是辛普森值序列 $\begin{Bmatrix} S_{2} \end{Bmatrix}$ ， $\begin{Bmatrix} T_{2}^{k} \end{Bmatrix}$ 就是科特斯值序列 $\begin{Bmatrix} C_{2} \end{Bmatrix}$ ， $\begin{Bmatrix} T_{3}^{k} \end{Bmatrix}$ 就是龙贝格值序列 $\begin{Bmatrix} R_{2} \end{Bmatrix}$

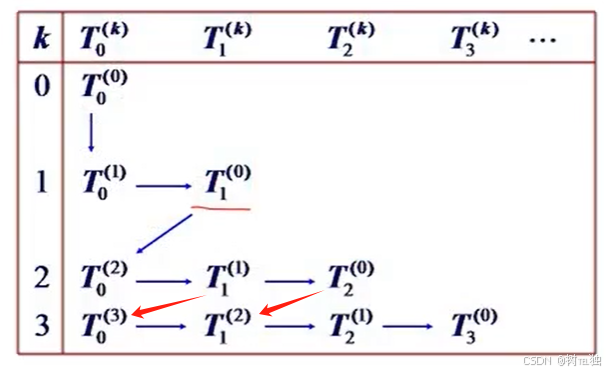
·理查森外推法

设 $I=\int_{a}^{b}f(x)dx$ 将区间 $[a,b]2^{k}$ 等分， $h=\frac{b-a}{2^{k}}$ ，记用复化梯形公式求得的近似值为 $T_{n}$ 记为 $T(h)$

注意到： $I-T(h)=-\frac{b-a}{12}h^{2}f^{''}(\eta )=O(h^{2})$ ，而 $lim_{h\rightarrow 0}T(h)=T(0)=I,T_{2n}=T(\frac{h}{2})$ ，

则 $T(h)=I+a_{1}h^{2}+a_{2}h^{4}+a_{3}h^{6}+\cdots ,$ $T(\frac{h}{2})=I+\frac{1}{2^{2}}a_{1}h^{2}+\frac{1}{2^{4}}a_{2}h^{4}+\frac{1}{2^{6}}a_{3}h^{6}+\cdots$

$\Rightarrow T_{1}(h)=\frac{4T(\frac{h}{2})-T(h)}{3}=I+b_{1}h^{4}+b_{2}h^{6}+\cdots$ ，即 $T_{1}(h)-I=O(h^{4})$

如此构造序列 $T_{1}(h),T_{1}(\frac{2}{h}),\cdots$ 就是辛普森序列 $S_{n},S_{2n},\cdots$

由 $T_{1}(h)=I+\beta _{1}\frac{h^{4}}{16}+\beta _{2}h^{6}+\cdots$ ，若令 $T_{2}(h)=\frac{16}{15}T_{1}(\frac{h}{2})-\frac{1}{15}T_{1}(h)\Rightarrow T_{2}(h)=I+\gamma _{1}h^{6}+\gamma _{2}h^{8}+\cdots$