本文介绍了高斯过程和贝叶斯优化的概念及其在机器学习中的应用。高斯过程是一种随机过程，当其有限维分布为正态分布时，常用于复杂函数的建模。贝叶斯优化则是在函数无解析表达或存在外界干预的情况下，寻找函数极值的一种策略，它通过高斯过程估计模型，并利用提取函数来指导采样。常见的提取函数包括Expected Improvement（EI）和Upper Confidence Bound（UCB），它们在探索与利用之间寻求平衡。
高斯过程（Gaussian process）
高斯过程常在论文里面简写为GP。定义：如果随机过程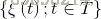
的有限维分布均为正态分布，则称此随机过程为高斯过程或正态过程。
首先我们来解读一下定义：
第一个问题：什么是随机过程？
大家都学过概率论，一定知道什么叫样本空间和随机变量（此处假设读者知道）。在概率论中，讲过样本空间，随机变量相当于是在样本空间中的一次采样，采样的结果是一个事件，在每次采样的时候都满足一定的分布。随机过程和随机变量的区别在于，样本空间里装的不是事件，装的是过程（一串事件）。每次的采样的结果是一个过程，比如一个序列，一个时间的函数等等。
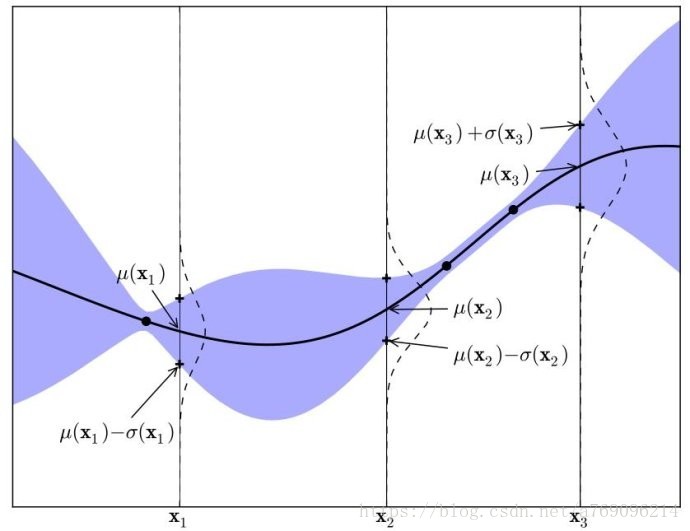
样本空间就是图中蓝紫色的部分，在蓝紫色空间中随便画一条函数，都是一个可能的随机过程。（这张图是盗用的“阿米斯丹猫的博客”）
第二个问题：什么是“随机过程的有限维分布均为正态分布”？
我们先来看一个随机序列：
这是一个有限维n的序列，我们可以理解为一个无穷维序列
进行的n次采样。
在这里可以理解为时间，但是更准确的应该理解为一个连续的指标集。因为其一般性，就可以看成的有限维分布。
所以“随机过程的有限维分布均为正态分布”就好理解了，即
最低0.47元/天 解锁文章
扫一扫
1216
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
