1.指数家族 (伯努利分布、泊松分布、高斯分布、贝塔分布、迪特利特分布等)
η:natural parameter
T(y) :sufficient statistic 充分统计量,(如果θ是总体样本的分布函数的参数,其充分统计量为t,则给定t的取值,样本的分布与θ无关)
a(η) log partition function,保证p(y;η)不同y值的概率加起来=1
T、a、b函数确定的话,就确定一种分布族(如伯努利分布),函数参数为η,η的取值不同表示同一分布族里面不同的分布(如伯努利分布里p(y=1|x)取值不一样)
2.伯努利分布的指数形式如下
因此
3.构造GLM
三个假设
(1)y|x;θ 满足如上形式的指数分布,参数为η
(2)我们要预测的目标是E[T(y)|x],即给定x,求T(y)。
当T(y)=y时,要学习的假设h(x)=E[y|x]
(3)η=θ ^T x
因此,当y|x:θ 满足伯努利分布时,h(x)=E[y|x]=Ф
4 Softmax Regression (T(y)多维)
例如 y可以取值1,2,3...,k,可看成k分类问题
则T(y)为k-1维向量
其概率分布








 本文介绍了指数家族的概念,包括常见的伯努利分布、泊松分布等,并解释了充分统计量和自然参数的作用。同时,文章详细阐述了如何利用这些概念构建广义线性模型(GLM),并以伯努利分布为例说明了如何进行预测。
本文介绍了指数家族的概念,包括常见的伯努利分布、泊松分布等,并解释了充分统计量和自然参数的作用。同时,文章详细阐述了如何利用这些概念构建广义线性模型(GLM),并以伯努利分布为例说明了如何进行预测。
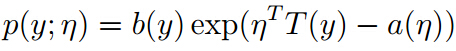
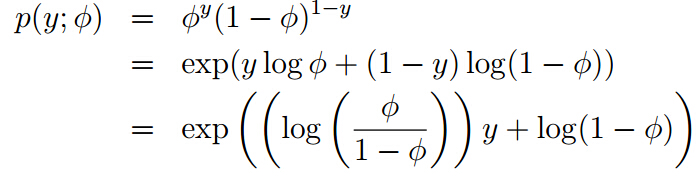
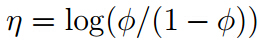
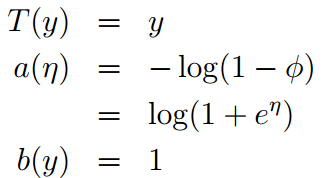
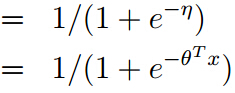
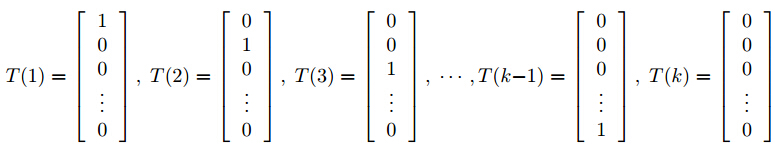
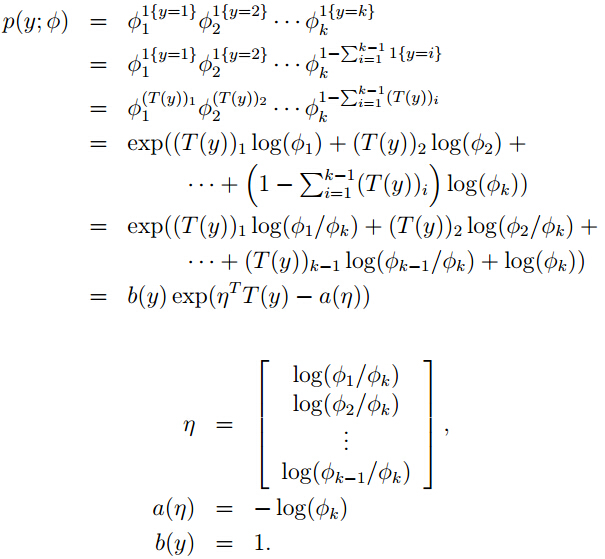

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








