Python 离群点检测算法 -- LOF详解

局部离群因子（LOF）是一种有效的无监督学习方法，它使用最近邻搜索来识别异常点，是一种基于密度的技术。在本章中，我将解释其动机和算法，并带领大家在 PyOD 中进行实践。基于密度的算法都对异常值很敏感，很容易出现过拟合，解决方法是训练多个模型，然后汇总得分。通过聚合多个模型，过拟合的几率会降低，预测精度也会提高。PyOD 模块提供了几种汇总结果的方法：平均法（Average）、最大值的最大值法（MOM）、最大值的平均值法（AOM）和平均值的最大值法（MOA）。在文中，我将只演示平均法。

离群点可以是全局性的，也可以是局部性的
离群点很容易感知，但用数学定义却不容易。相距甚远的数据点就是离群点。一次我在海滩岩石上看日落，一群海鸥站在我旁边的岩石上，有一只灰色的海鸥独自站在另一块岩石上。从我坐的地方看，那只灰色的海鸥是个异类。虽然海滩很长，海滩上还有很多其他的单身海鸥。从海滩的近处向远处看，那只灰色海鸥并不像离群的。

上述故事表明，离群点可能是全局离群点，也可能是局部离群点。数据点远离其附近的数据体时，会被视为离群值。图 (A) 展示了局部异常值和全局异常值。全局的算法可能只能捕捉到全局离群值。如果需要识别局部异常值，就需要一种能够关注局部邻域的算法。局部邻域中数据点的密度是关键，而 LOF 将不同密度的局部邻域纳入了识别局部离群值的考虑范围。

全局和局部离群值
LOF 如何工作？
LOF计算的是数据点相对于其相邻数据点的密度偏差，用于识别离群点。下图中a1点的密度远低于蓝色簇的点，显示蓝色聚类比绿色聚类更密集。当数据密度不同，LOF尤其有效。点a2是绿色聚类的局部离群点。LOF可以检测局部离群点。

局部离群因子（LOF）旨在调整不同局部密度的变化。它分为五个步骤，其中第四步涉及局部密度，第五步比较点的邻域密度与附近数据集群的密度。

Step 1: K-neighbors
Step 2: K-distance
Step 3: Reachability-distance (RD)
Step 4: Local reachability density (LRD)
Step 5: Local Outlier Factor of K-neighbor: LOF(k)

Reachability-distance
首先，K-近邻是指 K-近邻之前的圆周区域。在图 (B) 中，O点的第一、第二和第三近邻分别是p1、p2 和p3。虚线圆是 K=3 时 K 最近邻的面积。这一定义与 KNN 相同。
其次，K-distance(o) 是点O到 K 最近邻居的距离。该距离可以用欧氏距离或曼哈顿距离测量。
第三，点 O 的可达性距离是 K-distance*(o*)或任意点P 与O 之间距离的最大值。P2到O的距离为d(P2,O)，小于点P3到O 的距离，即 K-distance(o)。因此P2的 RD 为 K-distance(o)，即P3到O 的距离。

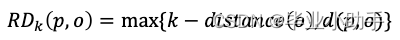
步骤 1 和 2 只是帮助定义步骤 3 中的可达性距离。可及距离公式是为了减少所有靠近O 点的点P的*d(p,o)*的统计波动。

在步骤 4 中，LRD 是O点与其邻居的平均可达距离的倒数。LRD 值低意味着最近的数据体远离O 点。

最后，在步骤 5 中，LOF 是点O的 K 个邻居的平均 LRD 与其 LRD 之比，如下式所示。第一项是 K 个邻居的平均 LRD。LOF 是p的 LRD 与点p的 K 个近邻的 LRD 之比的平均值。第二项是点O 的 LRD。

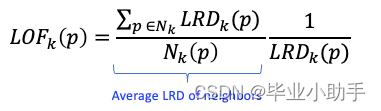
如果O点不是离群点，则邻近点的平均 LRD 与 O 点的 LRD 大致相等，此时 LOF 几乎等于 1。另一方面，如果O点是一个离群点，则第一期的邻居平均 LRD 将高于第二期，此时 LOF 将大于 1。

在 LOF 中使用距离比可以确保考虑到不同的局部密度。无论聚类密度如何，聚类中数据点的 LOF 值通常都接近于 1。例如，在图（A）中，蓝色或绿色聚类中数据点的 LOF 值都接近 1，尽管这两个聚类的密度不同。

一般来说，如果 LOF> 1，则被视为离群点。该数据点与相邻数据点的距离比预期的要远。另一方面，如果一个数据点位于数据密集区域，它就不是离群点。它的 LOF 值将接近 1。

建模流程
可以通过选择一个阈值来区分离群点得分高的异常观测值和正常观测值。如果先验知识表明异常值的百分比不应超过1%，那么您可以选择一个相应的阈值。

对于模型的合理性，两组之间特征的描述统计数据（比如均值和标准差）非常关键。如果预期异常组的某一特征平均值应该高于正常组，而结果恰恰相反，就需要对该特征进行调查、修改或放弃，并重新建模。

第一步：建立 LOF 模型
我将使用 PyOD 的generate_data()函数生成百分之十的离群值。数据生成过程（DGP）将创建六个变量，并且模拟数据集中包含目标变量 Y，但无监督模型只使用 X 变量。目的是为了增加案例的趣味性，异常值的百分比设置为 5%，“contamination=0.05”。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pyod.utils.data import generate_data
contamination = 0.05 # percentage of outliers
n_train = 500       # number of training points
n_test = 500        # number of testing points
n_features = 6      # number of features
X_train, X_test, y_train, y_test = generate_data(
    n_train=n_train, 
    n_test=n_test, 
    n_features= n_features, 
    contamination=contamination, 
    random_state=123)

X_train_pd = pd.DataFrame(X_train)
X_train_pd.head()

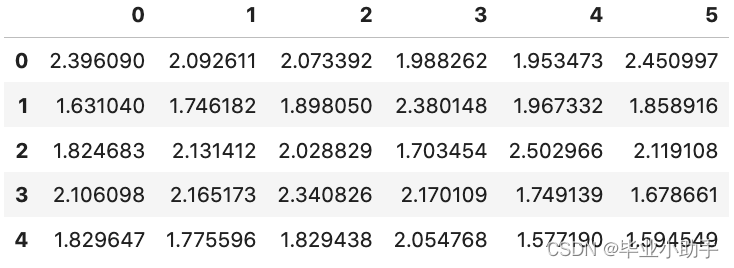
前两个变量绘制成散点图。散点图中的黄色点是百分之十的异常值。紫色点为正常观测值。

# Plot
plt.scatter(X_train_pd[0], X_train_pd[1