线性规划python

最新推荐文章于 2024-05-26 20:07:53 发布

平平平安喔

最新推荐文章于 2024-05-26 20:07:53 发布

阅读量6.1k

点赞数 4

文章标签： python 开发语言

本文链接：https://blog.csdn.net/abc1234564546/article/details/126248007

版权

线性规划

线性规划（Linear Programming 简记LP）是运筹学的一个重要分支，它起源于工业生产组织管理的决策问题，数学上它用来确定多变量线性函数在变量满足线性约束条件下的最优值。线性规划模型通常由三个要素—决策变量、目标函数和约束条件构成。一般来讲，决策变量是决策者为了达到预定目标而要控制的那些量，问题的求解就是找出决策变量的最终取值；

一、线性规划的概念和理论

1.线性规划一般模型

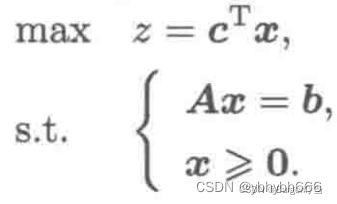
在这里插入图片描述

2.线性规划解的概念及理论

线性规划的基本点就是：在满足一定约束条件下使预定目标达到最优。

（1）可行解：满足全部约束条件的决策向量 x\in R^n 称为可行解；

（2）可行域：全部可行解构成的集合；

（3）最优解：使目标函数达到最优值（最大或最小值，并且有界）的可行解

定理：当线性规划问题有最优解时，一定可以在可行域的某个顶点上取到。当有唯一解时，最优解就是可行域的某个顶点。当有无穷多个最优解时，其中至少有一个解是可行域的一个顶点。

3.可转化为线性规划的问题

很多看起来不是线性规划的问题也可以通过变换转化为线性规划问题来求解，如问题
在这里插入图片描述
要把上面的问题转化成线性规划问题，主要注意到事实：对任意的xi，存在ui,vi>=0 满足

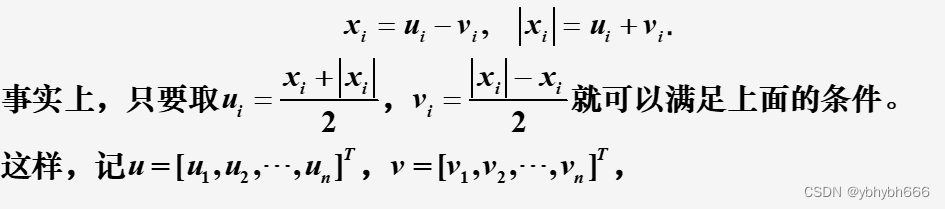
就可把上面的问题变成

二、线性规划的Python求解

1.用scipy.optimize模块求解

函数：linprog
在这里插入图片描述
注意：scipy中线性规划的标准型：

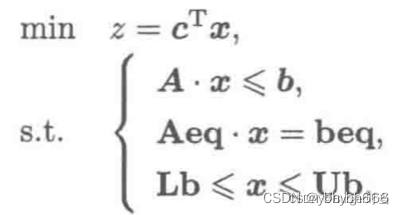
注意目标函数转化为求最小值（如果求最大值则等号两面加负号）

约束条件全部改成小于

1.1给个例题可以会明白一些

在这里插入图片描述

from scipy.optimize import linprog
c = [-1, 4]
A = [[-3, 1], [1, 2]]#类似系数矩阵
b = [6, 4]#类似结果矩阵
bound=((None,None),(-3,None))#x,y取值范围
res=linprog(c,A,b,None,None,bound)
print("目标函数的最小值：",res.fun)
print("最优解为：",res.x)

目标函数的最小值： -21.999999840824927
最优解为： [ 9.99999989 -2.99999999]
所以所求问题的最优解为：x1=10,x2=-3，目标函数最优值为-22

1.2.求下列线性规划问题

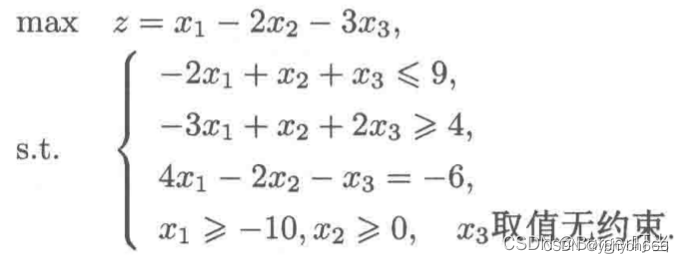
在这里插入图片描述
首化先为scipy标准型：

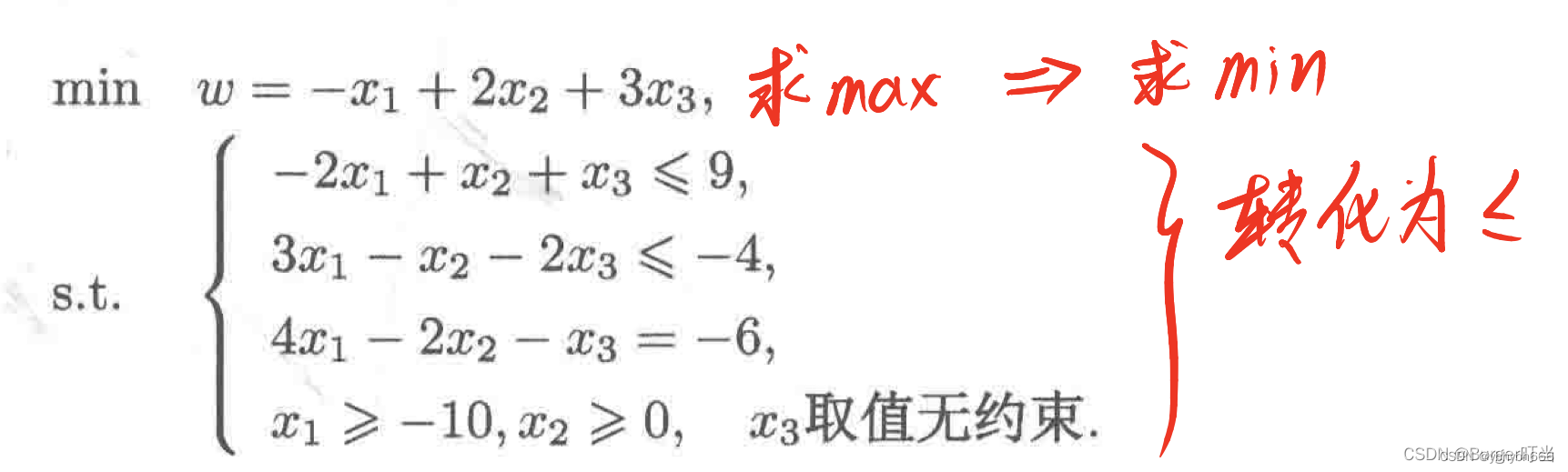
from scipy.optimize import linprog
c=[-1, 2, 3]; A = [[-2, 1, 1], [3, -1, -2]]
b=[[9], [-4]]; Aeq=[[4, -2, -1]]; beq=[-6]
LB=[-10, 0, None];
UB=[None]*len(c)  #生成3个None的列表
bound=tuple(zip(LB, UB))  #生成决策向量界限的元组
res=linprog(c,A,b,Aeq,beq,bound)
print("目标函数的最小值：",res.fun)
print("最优解为：",res.x)

在这里插入图片描述

1.3.在实际问题中应用

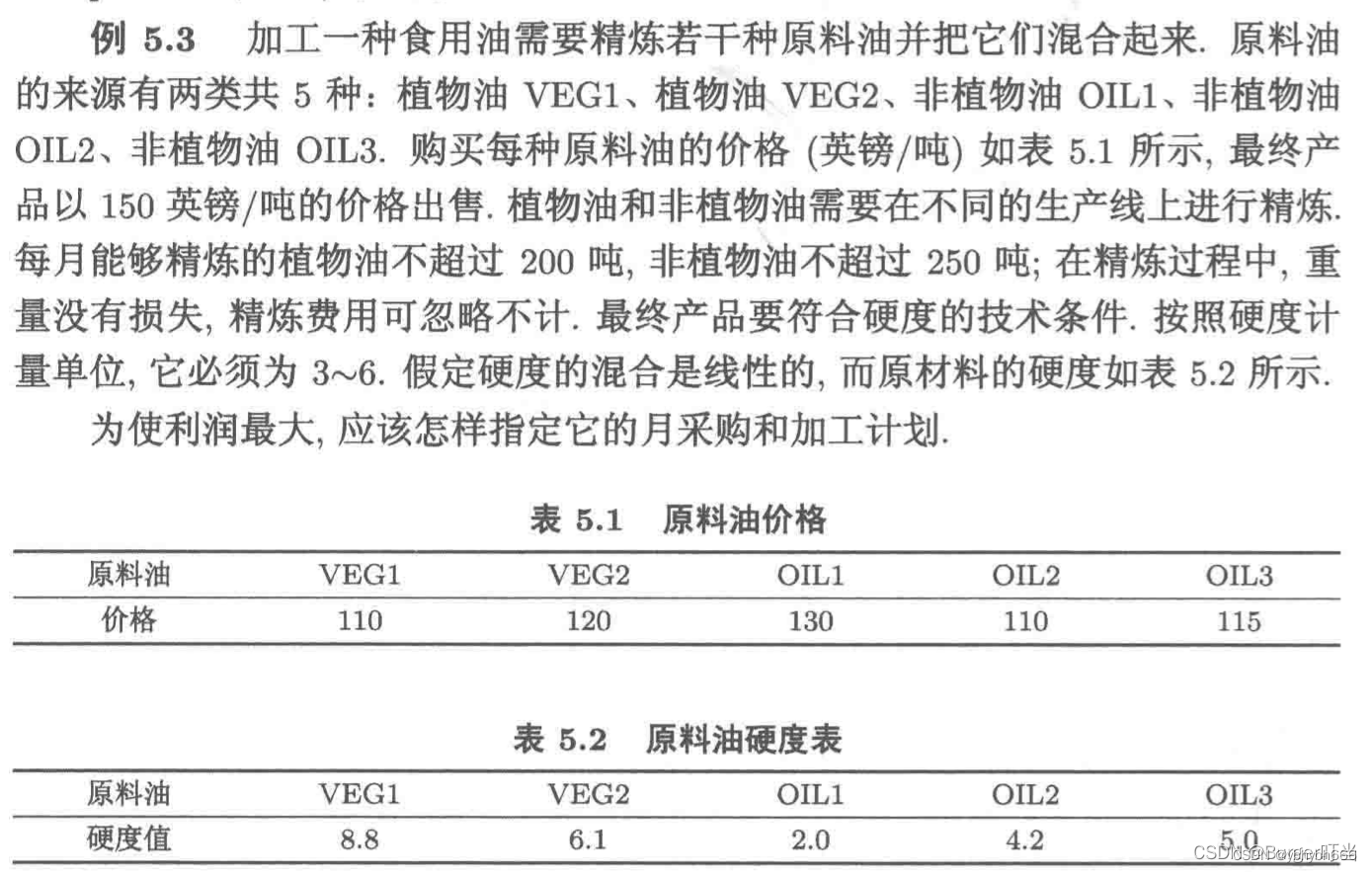
在这里插入图片描述

所以得到线性规划模型：

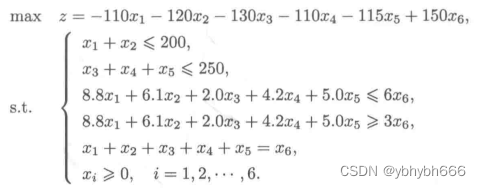
转化为python标准型：

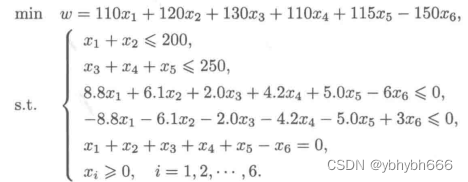
from scipy.optimize import linprog
c=[110, 120, 130, 110, 115,-150]    #目标向量
A =[[1,1,0,0,0, 0],[0,0,1,1,1,0],[8.8,6.1,2.0,4.2,5.0,-6],[-8.8,-6.1,-2.0,-4.2,-5.0,3]]
b=[[200],[250],[0],[0]]; Aeq=[[1,1,1,1,1,-1]]; beq=[0]
res=linprog(c,A,b,Aeq,beq)
print("目标函数的最小值：",res.fun)
print("最优解为：",res.x)

在这里插入图片描述

2.用cvxopt.solvers模块求解

cvxopt.solvers模块求解线性规划模型的标准型如下：
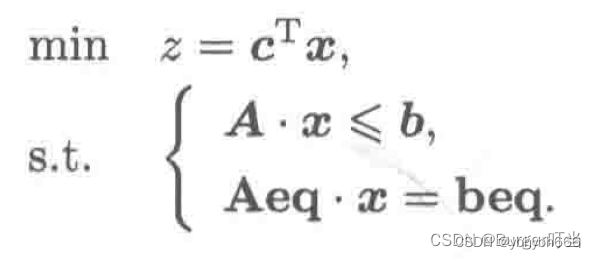
在这里插入图片描述

2.1求解线性规划：

在这里插入图片描述

import numpy as np
from cvxopt import matrix, solvers
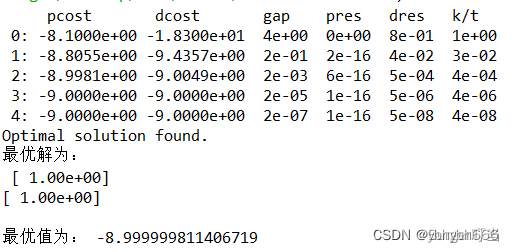
c=matrix([-4.,-5]); A=matrix([[2.,1],[1,2],[-1,0],[0,-1]]).T
b=matrix([3.,3,0,0]); sol=solvers.lp(c,A,b)
print("最优解为：\n",sol['x'])
print("最优值为：",sol['primal objective'])

在这里插入图片描述

2.2求解线性规划

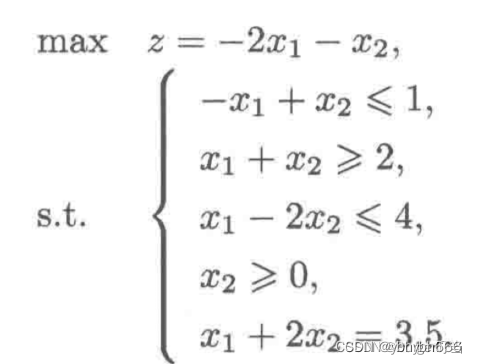
在这里插入图片描述
转化为标准型

import numpy
from cvxopt import matrix, solvers
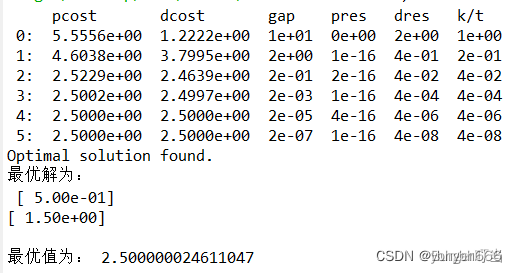
c=matrix([2.,1]); A=matrix([[-1.,1],[-1,-1],[1,-2],[0,-1]]).T
b=matrix([1.,-2,4,0]); Aeq=matrix([1.,2],(1,2)) #Aeq为行向量
beq=matrix(3.5); sol=solvers.lp(c,A,b,Aeq,beq)
print("最优解为：\n",sol['x'])
print("最优值为：",sol['primal objective'])

在这里插入图片描述

3 用cvxpy求解

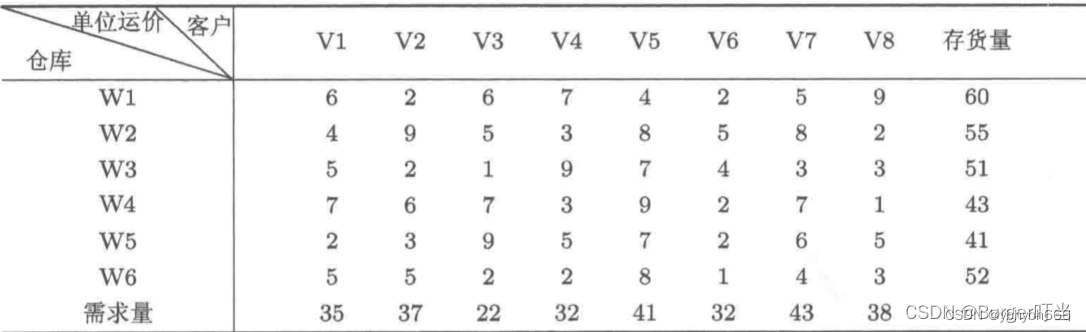
已知某种商品6个仓库的存货量，8个客户对该商品的需求量，单位商品运价如表5.4所示，试确定6个仓库到8个客户的商品调运数量，使总的运输费用最小。

在这里插入图片描述

import cvxpy as cp
import numpy as np
import pandas as pd
d1=pd.read_excel("Pdata5_6.xlsx",header=None)
d2=d1.values; c=d2[:-1,:-1]
d=d2[-1,:-1].reshape(1,-1); e=d2[:-1,-1].reshape(-1,1)
x=cp.Variable((6,8))
obj=cp.Minimize(cp.sum(cp.multiply(c,x)))  #构造目标函数
con=[cp.sum(x,axis=1,keepdims=True)<=e,
cp.sum(x,axis=0,keepdims=True)==d,x>=0]  #构造约束条件
prob=cp.Problem(obj,con)  #构造模型
prob.solve(solver='GLPK_MI',verbose=True)    #求解模型
print("最优值为：",prob.value)
print("最优解为：\n",x.value)