前言
关于位置编码和RoPE
- 应用广泛,是很多大模型使用的一种位置编码方式,包括且不限于LLaMA、baichuan、ChatGLM等等
- 我之前在本博客中的另外两篇文章中有阐述过(一篇是关于LLaMA解读的,一篇是关于transformer从零实现的),但自觉写的不是特别透彻好懂
再后来在我参与主讲的类ChatGPT微调实战课中也有讲过,但有些学员依然反馈RoPE不是特别好理解
考虑到只要花足够多的时间 心思 投入,没有写不清楚的,讲课更是如此,故为彻底解决这个位置编码/RoPE的问题,我把另外两篇文章中关于位置编码的内容抽取出来,并不断深入、扩展、深入,比如其中最关键的改进是两轮改进,一个12.16那天,一个12.21那天
- 12.16那天
小的改进是把“1.1 标准位置编码的起源”中,关于i、2i、2i+1的一系列计算结果用表格规整了下
如此,相比之前把一堆数字一堆,表格更加清晰、一目了然
大的改进是把“3.1.1 第一种形式的推导(通俗易懂版)”的细节重新梳理了以下,以更加一目了然、一看即懂,可能是全网关于RoPE最通俗细致的推导 - 12.21那天
把RoPE的本质给强调出来
最终成为本文
第一部分 transformer原始论文中的标准位置编码
如此篇文章《Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT》所述,RNN的结构包含了序列的时序信息,而Transformer却完全把时序信息给丢掉了,比如“他欠我100万”,和“我欠他100万”,两者的意思千差万别,故为了解决时序的问题,Transformer的作者用了一个绝妙的办法:位置编码(Positional Encoding)
1.1 标准位置编码的起源
即将每个位置编号,从而每个编号对应一个向量,最终通过结合位置向量和词向量,作为输入embedding,就给每个词都引入了一定的位置信息,这样Attention就可以分辨出不同位置的词了,具体怎么做呢?
- 如果简单粗暴的话,直接给每个向量分配一个数字,比如1到1000之间
- 也可以用one-hot编码表示位置

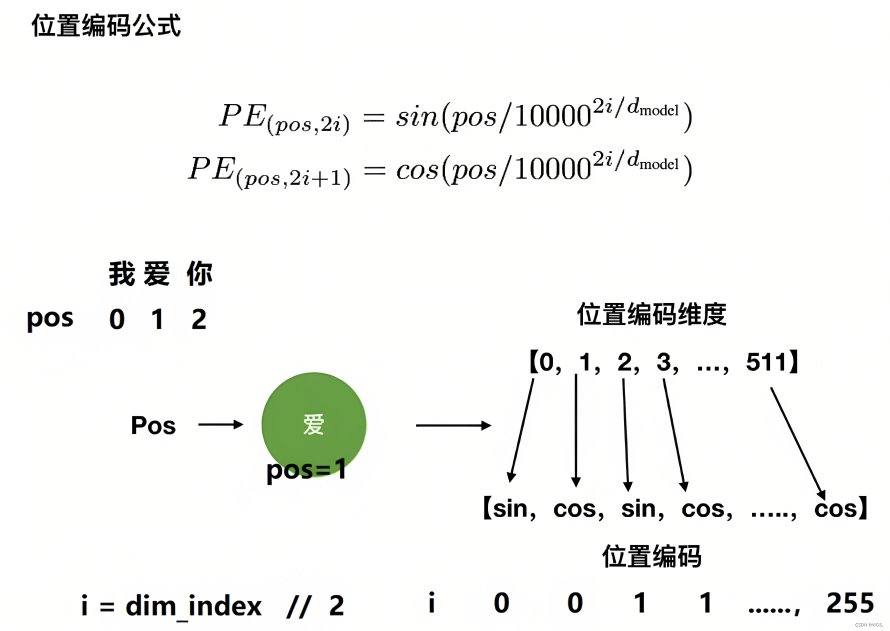
- transformer论文中作者通过sin函数和cos函数交替来创建 positional encoding,其计算positional encoding的公式如下
其中,pos相当于是每个token在整个序列中的位置,相当于是0, 1, 2, 3...(看序列长度是多大,比如10,比如100),代表位置向量的维度(也是词embedding的维度,transformer论文中设置的512维)
至于
是embedding向量的位置下标对2求商并取整(可用双斜杠
表示整数除法,即求商并取整),它的取值范围是
,比如
相当于位置向量的第多少维
(0 2 4等偶数维用sin函数计算)0 1 2 3 4 5 6 .... 510 511 是指向量维度中的偶数维,即第0维、第2维、第4维...,第510维,用sin函数计算
是向量维度中的奇数维,即第1维、第3维、第5维..,第511维,用cos函数计算
不要小看transformer的这个位置编码,不少做NLP多年的人也不一定对其中的细节有多深入,而网上大部分文章谈到这个位置编码时基本都是千篇一律、泛泛而谈,很少有深入,故本文还是细致探讨下
1.2 标准位置编码的示例:多图多举例
考虑到一图胜千言 一例胜万语,举个例子,当我们要编码「我 爱 你」的位置向量,假定每个token都具备512维,如果位置下标从0开始时,则根据位置编码的计算公式可得『且为让每个读者阅读本文时一目了然,我计算了每个单词对应的位置编码示例(在此之前,这些示例在其他地方基本没有)』
- 当对
上的单词「我」进行位置编码时,它本身的维度有512维
- 当对
上的单词「爱」进行位置编码时,它本身的维度有512维
然后再叠加上embedding向量,可得

- 当对
上的单词「你」进行位置编码时,它本身的维度有512维
- ....
最终得到的可视化效果如下图所示

1.3 标准位置编码的coding实现
代码实现如下
-
“”“位置编码的实现,调用父类nn.Module的构造函数”“”
-
class PositionalEncoding(nn.Module):
-
def __init__(
self, d_model, dropout, max_len
=
5000):
-
super(PositionalEncoding,
self).__init__()
-
self.dropout
= nn.Dropout(p
=dropout) # 初始化dropout层
-
-
# 计算位置编码并将其存储在pe张量中
-
pe
= torch.
zeros(max_len, d_model) # 创建一个max_len x d_model的全零张量
-
position
= torch.arange(
0, max_len).unsqueeze(
1) # 生成
0到max_len-
1的整数序列,并添加一个维度
-
# 计算div_term,用于缩放不同位置的正弦和余弦函数
-
div_term
= torch.exp(torch.arange(
0, d_model,
2)
*
-
-(math.log(
10000.0)
/ d_model))
-
-
# 使用正弦和余弦函数生成位置编码,对于d_model的偶数索引,使用正弦函数;对于奇数索引,使用余弦函数。
-
pe[:,
0
::
2]
= torch.sin(position
* div_term)
-
pe[:,
1
::
2]
= torch.cos(position
* div_term)
-
pe
= pe.unsqueeze(
0) # 在第一个维度添加一个维度,以便进行批处理
-
self.register_buffer(
'pe', pe) # 将位置编码张量注册为缓冲区,以便在不同设备之间传输模型时保持其状态
-
-
# 定义前向传播函数
-
def forward(
self, x):
-
# 将输入x与对应的位置编码相加
-
x
= x
+ Variable(
self.pe[:, :x.
size(
1)],
-
requires_grad
=
False)
-
# 应用dropout层并返回结果
-
return
self.dropout(x)
本文发布之后,有同学留言问,上面中的第11行、12行代码
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
为什么先转换为了等价的指数+对数运算,而不是直接幂运算?是效率、精度方面有差异吗?
这里使用指数和对数运算的原因是为了确保数值稳定性和计算效率
- 一方面,直接使用幂运算可能会导致数值上溢或下溢。当d_model较大时,10000.0 ** (-i / d_model)中的幂可能会变得非常小,以至于在数值计算中产生下溢。通过将其转换为指数和对数运算,可以避免这种情况,因为这样可以在计算过程中保持更好的数值范围
- 二方面,在许多计算设备和库中,指数和对数运算的实现通常比幂运算更快。这主要是因为指数和对数运算在底层硬件和软件中有特定的优化实现,而幂运算通常需要计算更多的中间值
所以,使用指数和对数运算可以在保持数值稳定性的同时提高计算效率。
既然提到了这行代码,我们干脆就再讲更细致些,上面那行代码对应的公式为

其中的中括号对应的是一个从 0 到 的等差数列(步长为 2),设为
且上述公式与这个公式是等价的
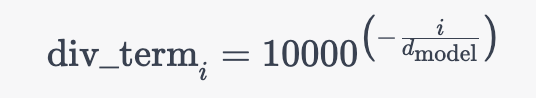
为何,原因在于,从而有
最终,再通过下面这两行代码完美实现位置编码
-
# 使用正弦和余弦函数生成位置编码,对于d_model的偶数索引,使用正弦函数;对于奇数索引,使用余弦函数。
-
pe[:,
0
::
2]
= torch.sin(position
* div_term)
-
pe[:,
1
::
2]
= torch.cos(position
* div_term)
第二部分 从复数到欧拉公式
先复习下复数的一些关键概念
- 我们一般用
表示复数,实数
叫做复数的实部,实数
叫做复数的虚部
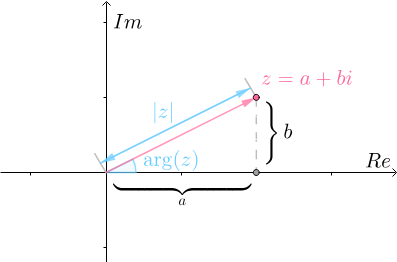
- 复数的辐角是指复数在复平面上对应的向量和正向实数轴所成的有向角

的共轭复数定义为:
,也可记作
,复数与其共轭的乘积等于它的模的平方,即
,这是一个实数
2.1 如何通俗易懂的理解复数
在我们的日常生活中,经常会遇到各种平移运动,为了描述这些平移运动,数学上定义了加减乘除,然还有一类运动是旋转运动,而加减乘除无法去描述旋转运动,而有了复数之后,便不一样了,此话怎讲?
根据复数的定义:,可以看出来:
,而这个展开过程就揭示了虚数
背后的本质,因为这个展开过程中的两次乘法可以看成连续的操作
- 即把 1 经过2次完全一样的操作:
,变成了 −1 ,那什么样的操作能得到这个效果呢?
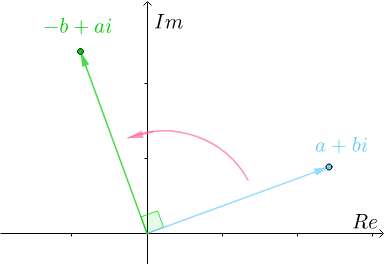
- 你两眼一亮,直呼:旋转啊,先旋转 90度,再旋转 90 度就可以了啊,如下图所示
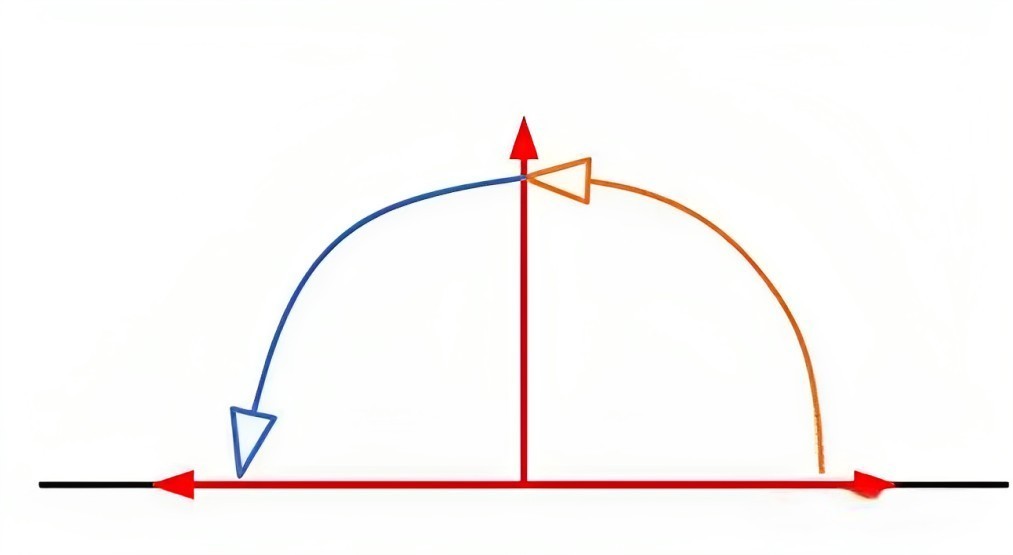
so, 就代表了旋转(至此,可能你已经隐隐约约意识到,为何我们在解释旋转位置编码时,为何要扯上复数了),为形象说明,再举两个例子
- 比如对于
,自然数 1,绕坐标中心旋转180度(
),再平移1 ,就回到坐标原点
- 再比如对于
2.2 如何快速理解欧拉公式
2.2.1 什么是欧拉公式
当 表示任意实数,
是自然对数的底数,
是复数中的虚数单位,则根据欧拉公式有
表达的含义在于该指数函数可以表示为实部为,虚部为
的一个复数
该欧拉公式相当于建立了指数函数、三角函数和复数之间的桥梁,但怎么推导出来的呢,其实很简单
- 由于有
- 所以,如果
,则有
2.2.2 欧拉公式与三角函数
如何直观的理解这个欧拉公式呢?
其实,可以把看作通过单位圆的圆周运动来描述单位圆上的点,
通过复平面的坐标来描述单位圆上的点,是同一个点不同的描述方式,所以有
,如下图所示
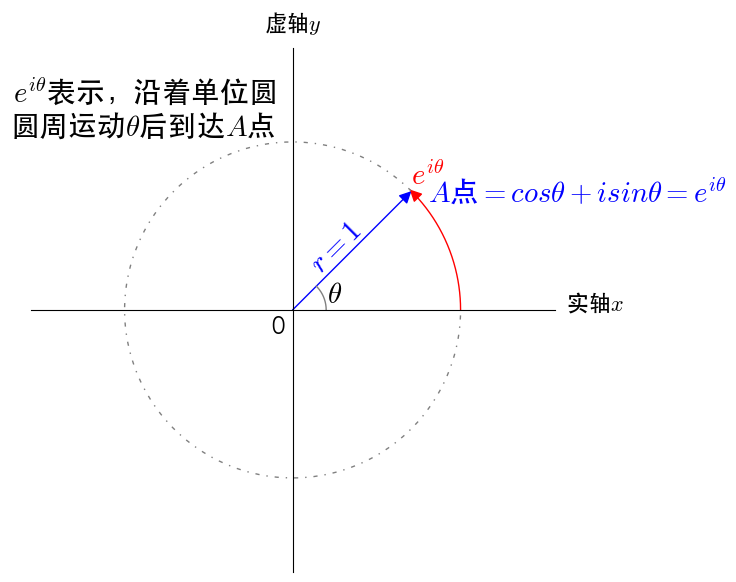
根据欧拉公式,可以轻易推出:
sinθ=eiθ−e−iθ2i),继续可知,我们现在要证明的是存在
g(xm,xn,






















 2274
2274











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








