网易的校招薪资。。。

数据结构和算法

于 2024-01-25 14:40:55 发布

阅读量1.3k

点赞数 20

本文链接：https://blog.csdn.net/abcdef314159/article/details/135857195

版权

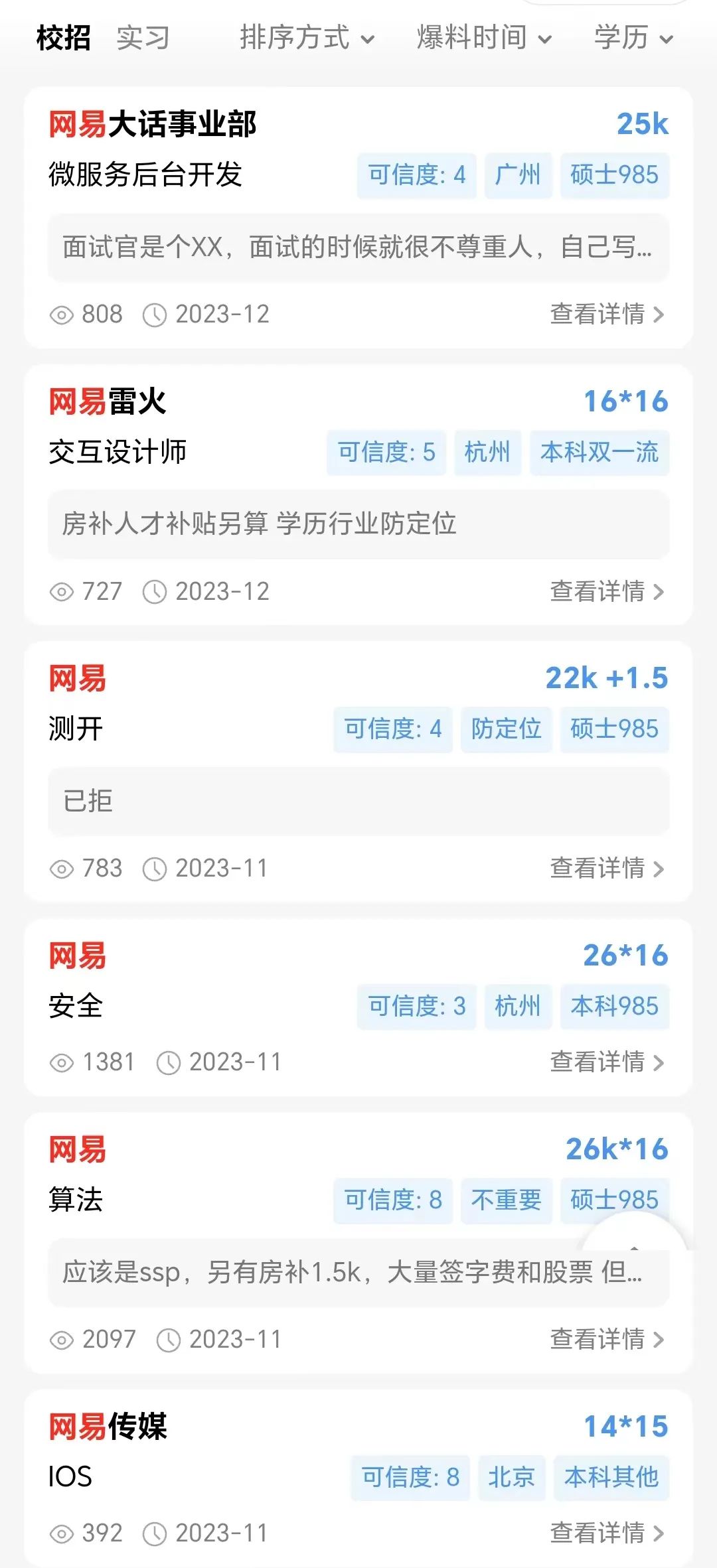
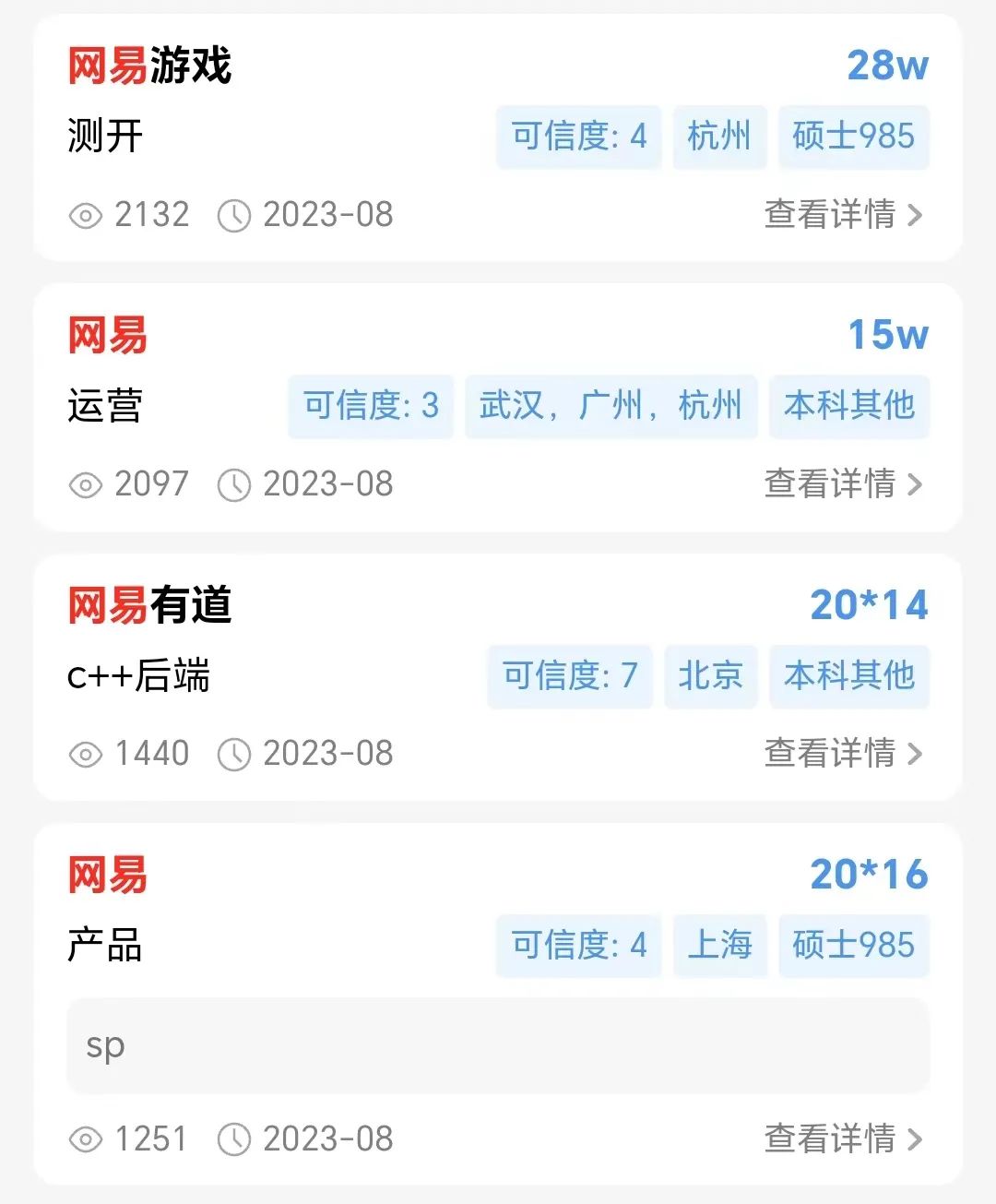
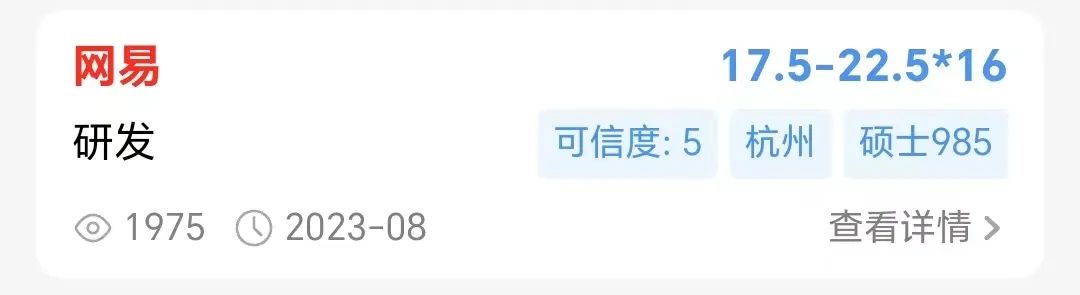
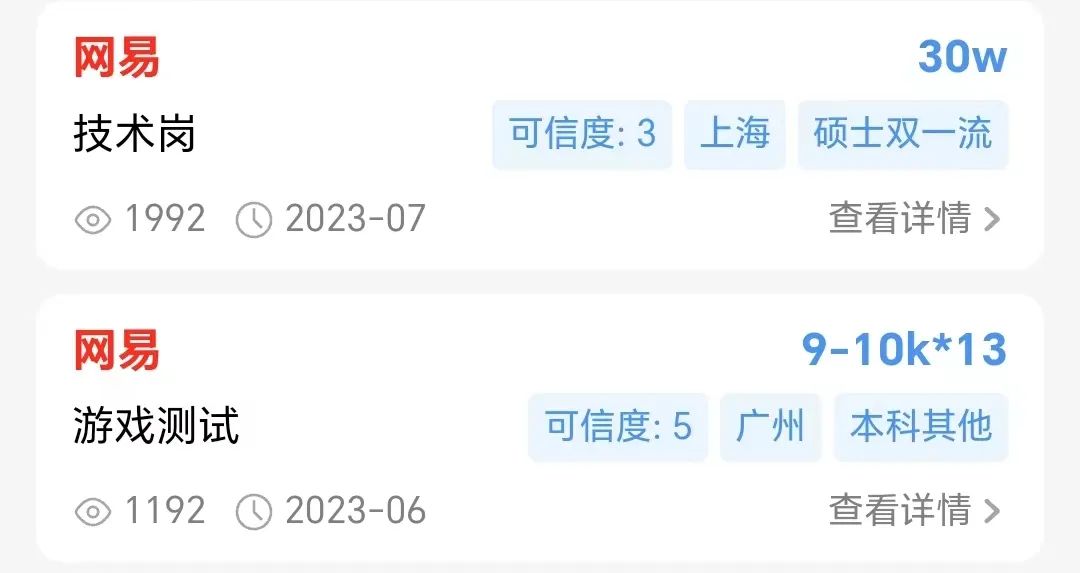
昨天我们看了网易裁员的消息，今天来看下网易的校招薪资，数据来源OfferShow，从薪资结构上来看16薪居多，对于开发岗来说年薪也能达到20w到30w，对于校招来说这个薪资不算少。但相比较我们之前看的字节，华为，腾讯等大厂的校招薪资确实差了一点。

--------------下面是今天的算法题--------------

我们今天继续看网易的面试题，这题是网易的第542题：01 矩阵，难度是中等，这题除了网易以外，字节也考过，我们来看下。

问题描述

来源：LeetCode第542题

难度：中等

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例1：

输入：mat = [[0,0,0],[0,1,0],[0,0,0]]

输出：[[0,0,0],[0,1,0],[0,0,0]]

示例2：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]

输出：[[0,0,0],[0,1,0],[1,2,1]]

m == mat.length
n == mat[i].length
1 <= m, n <= 10^4
1 <= m * n <= 10^4
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

动态规划解决

这题让计算的是每一个位置离他最近的0的距离，因为0到他自己的距离最短，值为0，我们不需要计算，这里只需要计算1到离他最近的0的距离即可。

提到最短最近等词我们首先想到的是BFS，当然这题使用BFS是可以解决的，除了使用BFS还可以使用动态规划来解决，我们来看下动态规划的解决思路。

定义dp[m][n]，其中dp[i][j]表示坐标（i，j）离他最近的0的距离。如果要计算坐标（i，j）离他最近的0的距离，那么这个距离肯定要经过他的上下左右4个方向中的一个，我们取最小的即可，也就是：

dp[i][j]=min(dp[i-1][j],dp[i+1][j],dp[i][j-1],dp[i][j+1])+1;

注意这里不能出现数组越界，但还有一个问题，就是如果我们从上往下遍历，当计算到dp[i][j]的时候，dp[i-1][j]和dp[i][j-1]的值已经计算过了，但dp[i+1][j]和dp[i][j+1]的值都还没有计算，所以这个时候我们需要两次遍历，先从上往下遍历一次，然后再从下往上遍历一次即可。

JAVA：

public int[][] updateMatrix(int[][] matrix) {
    int m = matrix.length, n = matrix[0].length;
    int[][] dp = new int[m][n];// 返回结果
    int max = m * n;
    // 从左上角开始
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (matrix[i][j] != 0) {// 当前位置只有1的时候才计算
                int up = i > 0 ? dp[i - 1][j] : max;// 上
                int left = j > 0 ? dp[i][j - 1] : max;// 左
                // 选择两个方向的最小值加1
                dp[i][j] = Math.min(up, left) + 1;
            }
        }
    }
    // 从右下角开始
    for (int i = m - 1; i >= 0; i--) {
        for (int j = n - 1; j >= 0; j--) {
            if (matrix[i][j] != 0) {// 当前位置只有1的时候才计算
                int down = (i < m - 1) ? dp[i + 1][j] : max;// 下
                int right = (j < n - 1) ? dp[i][j + 1] : max;// 右
                // 选择四个方向的最小。
                dp[i][j] = Math.min(Math.min(down, right) + 1, dp[i][j]);
            }
        }
    }
    return dp;
}

C++：

public:
    vector<vector<int>> updateMatrix(vector<vector<int>> &mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> dp(m, vector<int>(n));// 返回结果
        int max = m * n;
        // 从左上角开始
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (mat[i][j] != 0) {
                    int up = i > 0 ? dp[i - 1][j] : max;// 上
                    int left = j > 0 ? dp[i][j - 1] : max;// 左
                    // 选择两个方向的最小值加1
                    dp[i][j] = min(up, left) + 1;
                }
            }
        }
        // 从右下角开始
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                if (mat[i][j] != 0) {
                    int down = (i < m - 1) ? dp[i + 1][j] : max;
                    int right = (j < n - 1) ? dp[i][j + 1] : max;
                    // 选择四个方向的最小。
                    dp[i][j] = min(min(down, right) + 1, dp[i][j]);
                }
            }
        }
        return dp;
    }

C：

int min(int a, int b) {
    return a > b ? b : a;
}

int **updateMatrix(int **mat, int matSize, int *matColSize, int *returnSize, int **returnColumnSizes) {
    int n = *matColSize;
    *returnSize = matSize;
    *returnColumnSizes = matColSize;
    int max = matSize * n;
    int **dp = (int **) malloc(matSize * sizeof(int *));// 返回结果
    for (int i = 0; i < matSize; i++) {
        dp[i] = (int *) malloc(sizeof(int) * n);
        memset(dp[i], 0, sizeof(int) * n);// 初始化0
    }

    // 从左上角开始
    for (int i = 0; i < matSize; i++) {
        for (int j = 0; j < n; j++) {
            if (mat[i][j] != 0) {
                int up = i > 0 ? dp[i - 1][j] : max;// 上
                int left = j > 0 ? dp[i][j - 1] : max;// 左
                // 选择两个方向的最小值加1
                dp[i][j] = min(up, left) + 1;
            }
        }
    }
    // 从右下角开始
    for (int i = matSize - 1; i >= 0; i--) {
        for (int j = n - 1; j >= 0; j--) {
            if (mat[i][j] != 0) {
                int down = (i < matSize - 1) ? dp[i + 1][j] : max;
                int right = (j < n - 1) ? dp[i][j + 1] : max;
                // 选择四个方向的最小。
                dp[i][j] = min(min(down, right) + 1, dp[i][j]);
            }
        }
    }
    return dp;
}

Python：

def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
    m, n = len(mat), len(mat[0])
    dp = [[0] * n for _ in range(m)]  # 返回结果
    max = m * n
    # 从左上角开始
    for i in range(m):
        for j in range(n):
            if mat[i][j]:
                up = dp[i - 1][j] if i > 0 else max  # 上
                left = dp[i][j - 1] if j > 0 else max  # 左
                # 选择两个方向的最小值加1
                dp[i][j] = min(up, left) + 1

    # 从右下角开始
    for i in range(m - 1, -1, -1):
        for j in range(n - 1, -1, -1):
            if mat[i][j]:
                down = dp[i + 1][j] if i < m - 1 else max
                right = dp[i][j + 1] if j < n - 1 else max
                # 选择四个方向的最小。
                dp[i][j] = min(min(down, right) + 1, dp[i][j])
    return dp