ZOJ 3863 Paths on the Tree 树分治

题目链接：点击打开链接

题意：

给定n个点的树。 常量k

问：对于一对路径，如果公共点<=k则为合法。

问有多少个合法的路径。

{1-3, 2-4} 和 {2-4,1-3} 视为2个不同的路径对。

1-3, 3-1视为相同路径。

思路：

首先来得到一个O(n^3)的算法:

把问题转成=> 总方案数 - 公共点>k个的路径对数

显然公共点是连续的，所以公共点会组成一条路径，我们设为 x-y，则枚举x和y，就能得到公共的部分（当然要保证x-y的公共点数>k)

那么现在的问题是 以公共路径为x-y 的路径对有多少条。

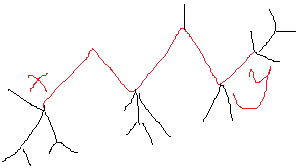
x有很多子树: x1, x2, x3 ···xi 图中为(1, 3, 3) 设sumx = x_1 + x_2 + ··+ x_i ( 这里sumx = 7

y有很多子树: y1, y2, y3···yi  图中为(1, 3, 1) 设sumy = y_1 + y_2 + ··+ y_i ( 这里sumy = 5

在x子树中选2个点排列的方案数 ans_x = (sum_x  - x_i) * x_i (for any i) + (sum_x-1)

（为何加上sum_x-1, 因为不同子树间的方案已经计算过2次，但一个点是x，另一点是子树节点的方案只计算了一次, 所以+ x_1 + x_2 +···+x_i = sum_x-1)

这样就能求出公共路径一端是x，选择2个点的方法数。

化简一下ansx = sumx * (sumx-1) - xi*xi + (sumx-1); 

我们设 fang = xi*xi;

则ansx = sumx*(sumx-1) - fang + (sumx-1);

进一步：

我们若要求出删除一个子树w后选2个点的方法数也就能简单地得到：

ansx' = (sumx - xi - w) * xi + (sumx-w-1) { i!=w } = (sumx-w) * (sumx-w-1) - (fang - w*w) + sumx-w-1;

剩下就是树分治。计算公共路径经过重心的方法数。

sum[cur][j] 表示对于当前枚举的重心的子树 ，子树中公共路径端点距离重心的距离恰好为 j 的个数。 相当于上述中的公共路径端点为X时，X端的方法数（即sumx)

sum[old][j] 表示以前枚举的重心的子树，子树中公共路径端点距离重心的距离>= j 的个数。同理相当于上述中公共路径端点为Y时

注意：

1、公共路径外的部分（即X子树中选的2个点，这两个点可以任意）可以经过重心，不能经过重心的只有公共部分的路径。

2、注意在找重心时算出的树的最大深度并不是 重心的最大深度。所以深度要持续更新。 

3、清空“后缀和”要多清一点，因为第二条的原因。

done..

/*
by:http://blog.csdn.net/acmmmm
*/
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <stack>
#include <time.h>
#include <queue>
template <class T>
inline bool rd(T &ret) {
	char c; int sgn;
	if (c = getchar(), c == EOF) return 0;
	while (c != '-' && (c<'0' || c>'9')) c = getchar();
	sgn = (c == '-') ? -1 : 1;
	ret = (c == '-') ? 0 : (c - '0');
	while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0');
	ret *= sgn;
	return 1;
}
template <class T>
inline void pt(T x) {
	if (x <0) {
		putchar('-');
		x = -x;
	}
	if (x>9) pt(x / 10);
	putchar(x % 10 + '0');
}
using namespace std;
typedef unsigned long long ll;
const int N = 100005;

struct Edge{
	int from, to, nex;
}edge[N << 1];
int head[N], edgenum;
void add(int u, int v){ Edge E = { u, v, head[u] }; edge[edgenum] = E; head[u] = edgenum++; }
int size[N], parent[N];
void dfs_init(int u, int fa){
	size[u] = 1; parent[u] = fa;
	for (int i = head[u]; ~i; i = edge[i].nex){
		int v = edge[i].to; if (v == fa)continue;
		dfs_init(v, u);
		size[u] += size[v];
	}
}
int n, k, maxdep;

int dp[N], num[N];//num[i]表示 以i为根的树 节点数  
//树重心的定义：dp[i]表示 将i点删去后 最大联通块的点数  
int root;
bool vis[N];
int siz;//** 表示当前 计算的树的节点数   
int G[N], top;
void getroot(int u, int fa, int deep){//找树的重心  
	dp[u] = 0; num[u] = 1;
	maxdep = max(maxdep, deep);
	for (int i = head[u]; ~i; i = edge[i].nex){
		int v = edge[i].to; if (v == fa || vis[v])continue;
		getroot(v, u, deep + 1);
		num[u] += num[v];
		dp[u] = max(dp[u], num[v]);
	}
	dp[u] = max(dp[u], siz - num[u]);
	if (dp[u] < dp[root])root = u;
}

ll ans, sum[2][N], w[N];
int dep[N];
ll Siz(int u, int v){
	if (v == parent[u])return size[u];
	else return n - size[v] ;
}
void dfs(int u, int fa, int deep){
	dep[u] = deep; maxdep = max(maxdep, deep);
	w[u] = Siz(u, fa) * (Siz(u, fa) - 1);
	num[u] = 1;
	G[top++] = u;
	for (int i = head[u]; ~i; i = edge[i].nex){
		int v = edge[i].to; if (v == fa)continue;
		w[u] -= Siz(v, u) * Siz(v, u);
		if (vis[v])continue;
		dfs(v, u, deep + 1);
		num[u] += num[v];
	}
	w[u] += Siz(u, fa);
}
void work(int u){
	siz = num[u];
	root = maxdep = 0;
	getroot(u, u, 0);
	if (maxdep * 2 < k)return;
	int old = 1, cur = 0;
	fill(sum[cur], sum[cur] + maxdep + 10, 0);
	sum[cur][0] = 1;
	ll all = n, fang = 0;
	for (int i = head[root]; ~i; i = edge[i].nex){
		int v = edge[i].to;
		fang += Siz(v, root) * Siz(v, root);
	}

	for (int i = head[root], j; ~i; i = edge[i].nex){
		int V = edge[i].to; if (vis[V])continue;
		top = 0;
		dfs(V, root, 1);
		swap(old, cur);
		fill(sum[cur], sum[cur] + maxdep + 10, 0);
		
		for (j = 0; j < top; j++) sum[cur][dep[G[j]]] += w[G[j]];
		for (j = 0; j <= maxdep; j++)
		{
			if (k-j <= maxdep)
			ans += sum[cur][j] * sum[old][max(0, k-j)];
		}
		for (j = maxdep-1; j >= 0; j--) sum[cur][j] += sum[cur][j + 1];
		if (k <= maxdep)
			ans += sum[cur][k] * (all - Siz(V, root) - 1 + (all - Siz(V, root)) * (all - Siz(V, root) - 1) - (fang - Siz(V, root)*Siz(V, root)));
		for (j = maxdep; j >= 0; j--)sum[cur][j] += sum[old][j];
	}
	vis[root] = true;
	for (int i = head[root]; ~i; i = edge[i].nex)
	if (false == vis[edge[i].to]) work(edge[i].to);
}

int main(){
	dp[0] = N;
	int T; rd(T);
	while (T--){
		rd(n); rd(k);
		memset(head, -1, sizeof head); edgenum = 0;
		for (int i = 1, u, v; i < n; i++){
			rd(u); rd(v); add(u, v); add(v, u);
		}
		dfs_init(1, 1);		
		ans = 0;
		num[1] = n;
		memset(vis, 0, sizeof vis);
		work(1);
		ll all = (ll)n*(n + 1) / 2;
		cout << (all * all - ans) << endl;
	}
	return 0;
}
/*
991

6 3
1 2
2 3
2 4
1 5
5 6

4 1
1 2
2 3
3 4

6 1
1 2
1 3
1 4
2 5
5 6

6 1
1 2
1 3
1 4
3 5
3 6

5 1
1 2
1 3
3 4
4 5


6 2
1 2
2 3
3 4
3 5
4 6

3 2
1 2
1 3

5 1
1 2
1 3
1 4
2 5


*/