数据结构入门——时间复杂度和空间复杂度

> 1. 时间复杂度：

时间复杂度实际上就是一个函数，计算程序执行的总次数（不是计算时间，是计算语句执行次数）；** 在进行时间复杂度计算时要注意：
1）在实际中通常考虑的是算法运行的最坏情况；
2）关注运行时间的增长趋势，关注增长最快的项即可，其他可进行忽略
比如：F（n)=8*n^2+9*n+9;其时间复杂度为O（n^2);
3)递归算法的时间复杂度计算：递归总次数*每次递归操作数

2、空间复杂度

它是对一个算法在运行过程中临时占用存储空间大小的量度，强调的是使用辅助空间的大小，不是所有的数据所占用的空间，不会一直累加。
（计算的不是空间，而是函数中创建的对象的个数） 递归算法的空间复杂度：
递归总次数为n*每次递归的辅助空间大小。若每次递归的辅助空间大小为常数， 则其空间复杂度为O（n)

咱们用以下实例来分析以下时间复杂度与空间复杂度**

1. 折半查找—–非递归

#include<stdio.h>
#include<stdlib.h>
int BinarySearch(int arr[],int sz,int n)
{
    int left=0;
    int right=sz-1;
    while(left<=right)
   {
    int mid=left+((right-left)>>1);
     if(arr[mid]>n)
     {
         right=right-1;
     }
     else if(arr[mid]<n)
     {
         left=left+1;
     }
     else
     {
         return mid;
     }

   }
    return -1;
}
int main()
{
    int arr[]={1,2,3,4,5,6,7,8,9};
    int sz=sizeof(arr)/sizeof(arr[0]);
     printf("%d\n", BinarySearch(arr,sz,1));
    printf("%d\n",  BinarySearch(arr,sz,2));
    printf("%d\n",  BinarySearch(arr,sz,3));
    printf("%d\n",  BinarySearch(arr,sz,4));
    printf("%d\n",  BinarySearch(arr,sz,5));
    printf("%d\n",  BinarySearch(arr,sz,6));
    printf("%d\n",  BinarySearch(arr,sz,7));
    printf("%d\n",  BinarySearch(arr,sz,8));
    printf("%d\n",  BinarySearch(arr,sz,9));
    system("pause");
    return 0;
}
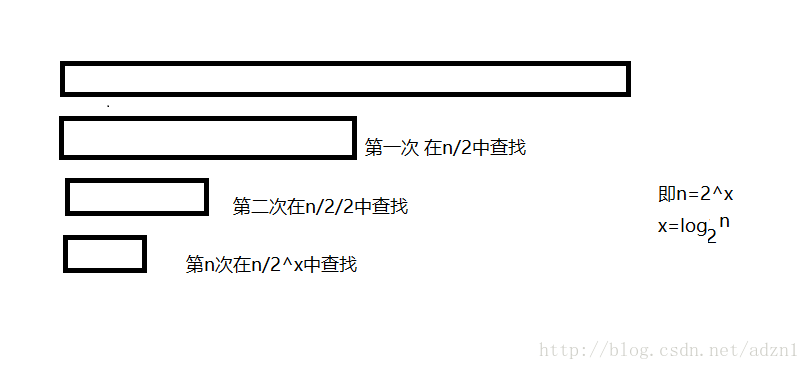
时间复杂度：O（log2 N)//每次查找缩小一半范围，即每次运行的次数为log2 N所以不难算出时间复杂度为----->O（log2 N）
空间复杂度：O(1)   创建的对象为常数个

折半查找——-递归

#include<stdio.h>
#include<stdlib.h>
int  BinarySearch(int arr[],int left,int right,int n)
{
    int mid=left+((right-left)>>1);
    while(left<=right)
    {
        if(arr[mid]==n)
        {
            return mid;
        }
        else if(arr[mid]>n)
        {
            return BinarySearch(arr,left,mid-1,n);
        }
        else if(arr[mid]<n)
        {
            return BinarySearch(arr,mid+1,right,n);
        }
    }
    return -1;
}
int main()
{
    int arr[]={1,2,3,4,5,6,7,8,9};
    int left=0;
    int sz=sizeof(arr)/sizeof(arr[0]);
    int right=sz-1;
    printf("%d\n",  BinarySearch(arr,left,right,1));
    printf("%d\n",  BinarySearch(arr,left,right,2));
     printf("%d\n", BinarySearch(arr,left,right,3));
     printf("%d\n", BinarySearch(arr,left,right,4)); 
     printf("%d\n", BinarySearch(arr,left,right,5));
     printf("%d\n", BinarySearch(arr,left,right,6));
     printf("%d\n", BinarySearch(arr,left,right,7));
     printf("%d\n", BinarySearch(arr,left,right,8));
     printf("%d\n", BinarySearch(arr,left,right,9));

    system("pause");
     return 0;
}
时间复杂度：递归总次数log2 N，每次执行的时间复杂度为O（1）------>O(log2  N)
空间复杂度：递归总次数log2 N，每次创建的对象都是常数个--------->O(log2   N)

斐波那锲数——-非递归

int fib(int n)//1 1 2 3 5 8 13
{
    int first=1;
    int second=1;
    int sum=0;
    if(n<3)
    {
        return 1;
    }
    while(n>2)
      {
          sum=first+second;
          first=second;
          second=sum;
          n--;
      }


   return  sum;
}
时间复杂度：O（N)---程序运行n次
空间复杂度：O(1)---创建的对象为常数个

斐波那锲数—递归

 long long fib(int n)
    {
        if(n<3)
            return 1;
        else
            return fib(n-1)+fib(n-2);
    }

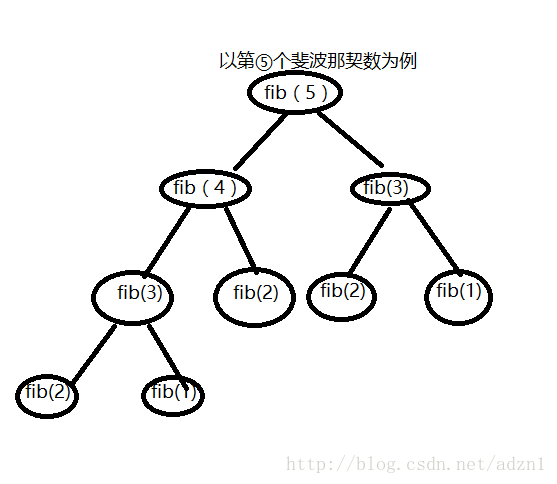
    每一次的计算都被分成前两个数之和，依次往下递归，类似于二叉树
    当n较大时，形成一个满二叉树

    时间复杂度：O（2^n)
    空间复杂度：O(n)