AVL树

AVL树

1.AVL树

    AVL树又称为高度平衡的二叉搜索树，它能保持二叉树的高度平衡，尽量降低二叉树的高度，减少树的平均搜索长度。

2.搜索树的性质

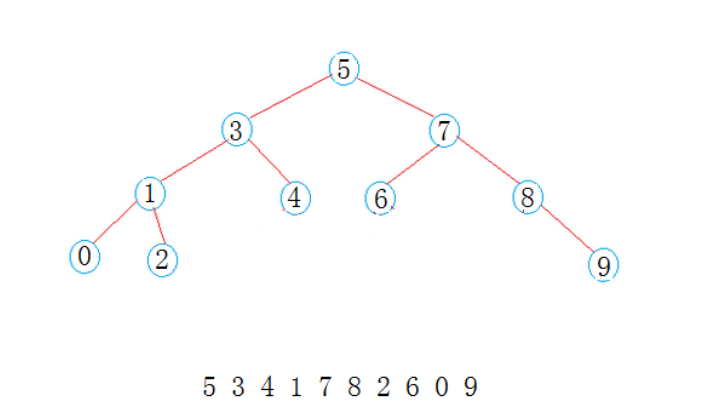
1）每个节点都有一个作为搜索依据的关键码（key），所有节点的关键码互不相同

2）左子树上所有节点的关键码都小于根节点的关键码

3）右子树上所有节点的关键码都大于根节点的关键码

4）左右子树都是二叉搜索树

如下图

3.AVL树的性质

1）左子树和右子树的高度之差绝对值不超过1

2）树中每个左子树和右子树都是AVL树

3）每个节点都有一个平衡因子，任一节点的平衡因子是0,1，-1（每个节点的平衡因子等于右子树的高度减去左子树的高度）

4.AVL树的效率

   一棵AVL树有N个节点，其高度可以保持在，插入、删除和查找的时间复杂度也是

5.AVL树的插入

  AVL树在插入的时候不仅要考虑有关搜索树方面的关键码的插入和调整，也要根据平衡因子进行旋转调整高度差

  平衡因子的调整：

1）新节点插入在父节点的右边时，父节点的平衡因子+1

2）新节点插入在父节点的左边时，父节点的平衡因子-1

当平衡因子等于2或者-2时，要对当前子树进行旋转

1）右单旋（当新节点插入在父节点的左孩子时）

2）左单旋

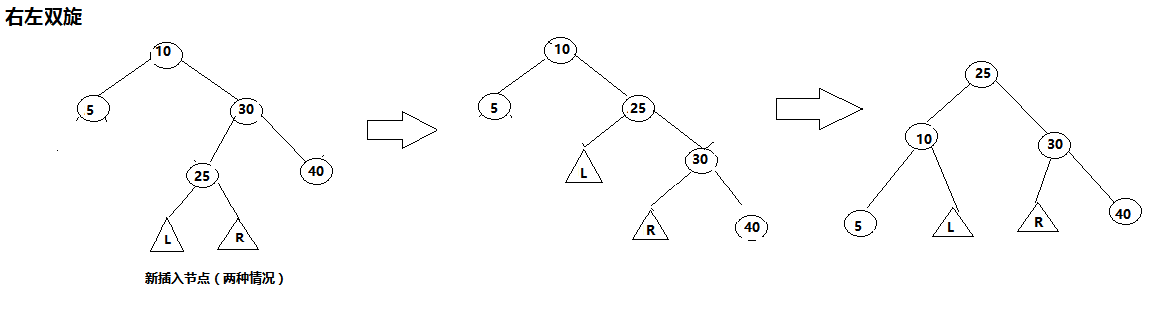
3）右左双旋

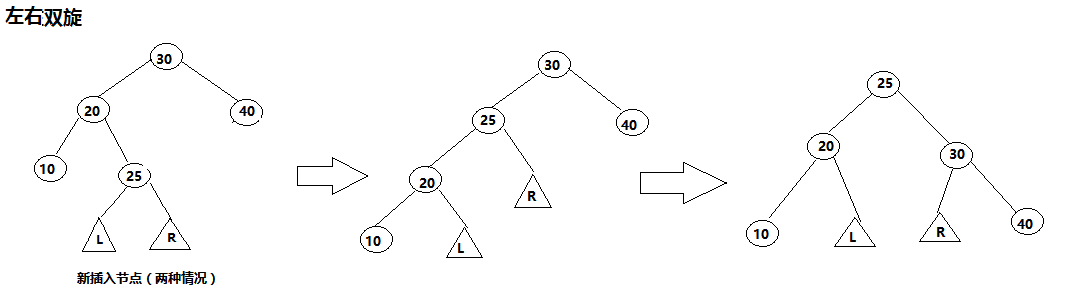
4）左右双旋

6.AVL树的节点结构

7.后记

   写这篇博客的目的只是想要着重写插入新节点时发生的旋转，所以也就之间旋转部分的函数贴出来。

1）右单旋

2）左单旋

3）右左双旋

4）左右双旋

   想看完整代码的可以去我的GitHub中查看：https://github.com/zknn/VS2013---Copy/blob/AVL树/AVLTree/AVLTree.h