空间运动模式的几何必然性与物理自洽性

空间运动模式的几何必然性与物理自洽性

——论张祥前统一场论中空间右手光速圆柱状螺旋运动的唯一性

摘要

空间的本质是物理学的核心问题。张祥前统一场论提出了革命性的空间运动模型：空间以右手、圆柱状、光速螺旋运动，而非其他形式。本文基于该理论的第一性原理——垂直原理，从几何必然性、物理自洽性及宇宙观测事实三个维度，系统论证了空间运动模式选择的唯一性与必然性。研究表明：空间以右手、圆柱状、光速螺旋运动，是该理论框架下满足三维空间几何属性、保证物理定律协变性、并与可观测宇宙现象相一致的唯一且必然的选择。 圆锥螺旋或其他模式，在几何上无法满足“垂直原理”，在物理上无法导出稳定的质量定义与平方反比引力定律，且与宇宙的均匀性及各向同性观测严重冲突。本文的论证不仅深化了对统一场论核心概念的理解，也为空间本质的研究提供了新的思路与方法。

关键词

统一场论；空间运动；垂直原理；圆柱状螺旋；光速；右手螺旋；几何必然性；物理自洽性；平方反比定律；宇称不守恒

一、引言

空间的本质是物理学中最古老、最深刻的问题，贯穿于整个物理学发展历程。从牛顿的绝对空间，到爱因斯坦相对论中与时间不可分割的四维时空，再到量子场论中充满涨落的量子真空，人类对空间的认识不断深化，但仍未达成最终统一。

张祥前统一场论提出了一个革命性的空间观：空间不是静止的背景，而是以特定模式运动的实体。这一观点突破了传统物理学将空间视为"舞台"的局限，将空间本身视为动力学系统，为实现物理学的大统一提供了新的思路。

该理论的核心假设是：空间以右手、圆柱状、光速螺旋运动。这一假设引发了广泛讨论，其中一个关键问题是：为什么空间必须是这种特定的运动模式，而非其他形式（如圆锥螺旋）？ 这一问题的解答对于验证统一场论的合理性至关重要。

本文基于统一场论的第一性原理——垂直原理，从几何必然性、物理自洽性及宇宙观测事实三个维度，系统论证空间运动模式选择的唯一性与必然性。研究表明，空间以右手、圆柱状、光速螺旋运动，是该理论框架下满足三维空间几何属性、保证物理定律协变性、并与可观测宇宙现象相一致的唯一且必然的选择。

本文的论证不仅为统一场论的核心概念提供了坚实的理论基础，也为空间本质的研究开辟了新的方向，有望推动物理学的进一步发展。

二、几何必然性：垂直原理与三维空间的运动模式

2.1 垂直原理：三维空间的第一性原理

张祥前统一场论的第一性原理是垂直原理（亦称三维垂直性公设），其表述为：

相对于任一观察者，宇宙中任意一点的空间，必须能且仅能作出三条相互垂直的直线（或运动轨迹的切线）。

这是三维空间的基本几何属性，也是所有三维空间理论的基础。任何描述空间运动的理论，都必须满足这一几何约束。

2.2 空间运动形式的几何推导

根据垂直原理，我们可以推导出空间点的运动形式：

2.2.1 一维与二维运动的局限性

• 直线运动：轨迹上任一点只能作出一条切线（运动方向），对应一维空间，无法满足三维空间的要求。
• 圆周运动：轨迹上任一点可作出两条相互垂直的切线（切向与法向），对应二维空间，同样无法满足三维空间的要求。

2.2.2 三维运动的必然选择：圆柱状螺旋运动

要满足三维空间的要求，空间点的运动轨迹必须在某点能作出三条相互垂直的切线。最简单的、满足各向同性基本要求的运动，就是圆柱状螺旋运动。

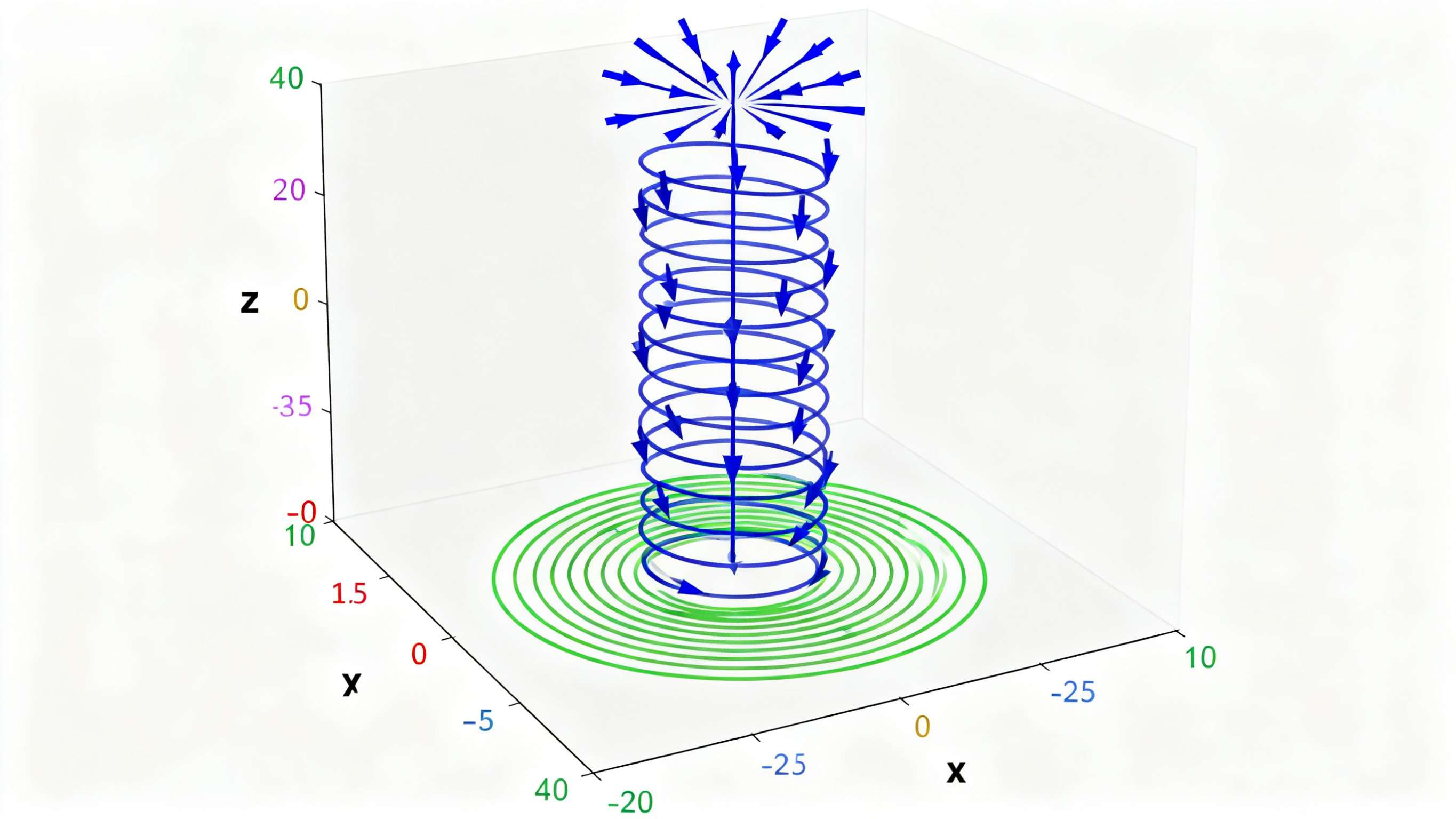
圆柱状螺旋运动的几何特征：

• 轨迹上任一点的切线方向（运动方向）
• 主法线方向（指向曲率中心）
• 副法线方向（平行于中心轴）

这三个方向恰好构成两两垂直的三维坐标系，完美满足垂直原理的要求。

2.3 圆锥螺旋的几何缺陷

圆锥螺旋线虽然也是三维曲线，但其几何结构存在根本性缺陷：

1. 曲率半径变化：圆锥螺旋线的曲率半径随轴向位置变化，其法线方向并不恒定。
2. 缺乏稳定的三维正交系：在圆锥螺旋线上，无法在任意点都全局性地、稳定地构造出三条相互垂直且方向恒定的切线方向来满足空间的各向同性基础。
3. 对称性缺失：圆锥螺旋缺乏圆柱螺旋的平移对称性（螺距恒定）和旋转对称性。
4. 几何基础不稳定：圆锥螺旋是特定条件下的变形，而非空间自身的本底运动形式。

2.4 结论一：圆柱状螺旋的几何必然性

从维系空间三维性的"垂直原理"出发，圆柱状螺旋是满足过任意一点可作三条相互垂直切线这一几何约束的最简单、最必然的运动形式。它是三维空间自身属性的直接体现，而非任意假设。圆锥螺旋无法作为描述空间基本运动模式的稳定、各向同性的几何基础，它是特定条件下的变形，而非空间自身的本底运动形式。

三、物理自洽性：光速与稳定运动模式的必要性

3.1 光速：时空同一化的定义常数

统一场论的核心公设是：空间点的运动合成速度恒为矢量光速 $C$，其大小恒为 $c$（真空中光速）。

3.1.1 光速的定义性本质

光速 $c$ 在此并非测量值，而是定义性常数：它是时空同一化方程 $\vec{R}=\vec{C}t$ 中的比例常数。时间 $t$ 被定义为光速运动的空间位移 $\vec{R}$ 的度量。因此，光速 $c$ 是连接时空的几何常数，是理论的原点。

3.1.2 速度三角形约束

空间点的运动可分解为旋转速度分量 $v_{rot}$ 和 直线速度分量 $v_{lin}$ ，满足：

$$v_{rot}^2+v_{lin}^2=c^2$$

这一"速度三角形"约束是理论的核心数学结构，保证了光速不变原理的自然满足。

3.2 稳定运动模式：质量定义的基础

空间运动模式的稳定性（即运动模式不随距离改变）是保证理论能推导出所有已知物理定律的关键。

3.2.1 质量的几何化定义

统一场论对质量的几何化定义是：

$$m=k\cdot \frac{n}{\Omega }$$

其中：

• $n$ 是空间位移矢量条数
• $\Omega$ 是立体角
• $k$ 是量子几何常数

3.2.2 立体角的关键作用

立体角 $\Omega$ 是描述方向范围的几何量，对于以点源为中心的球面，其总立体角为 $4\pi$，且不随距离 $r$ 变化。这一特性是定义内禀质量的关键。

3.2.3 圆锥螺旋对质量定义的破坏

如果空间运动是"圆锥"状发散，其有效"立体角"将随距离变化且难以明确定义。这种情况下，质量定义 $m=k\cdot \frac{n}{\Omega }$ 将失去物理意义，因为 $\Omega$ 不再是与距离无关的内禀量。

3.2.4 与平方反比定律的兼容

从该运动模式推导牛顿万有引力定律时，关键一步是利用了球面几何关系：

$$dS=r^{2}d\Omega$$

引力场强度正比于单位面积上穿过的空间位移线密度。由于圆柱状螺旋运动在统计意义上是球对称发散的，才能利用此球面关系，自然导出力与距离平方成反比 ($1/r^2$) 的形式。

圆锥螺旋的发散模式是非球对称的，将破坏这一关键推导，无法得到与实验观测相符的平方反比引力定律。

3.3 结论二：光速与稳定运动模式的物理必然性

只有以恒定光速 $c$进行的、模式稳定（各向同性、球对称统计分布）的圆柱状螺旋运动，才能通过立体角 $\Omega$ 定义出内禀质量，并利用球面几何自然导出平方反比引力定律等经典物理规律。圆锥螺旋在此完全失败，因为它无法提供稳定的、与距离无关的几何度量基础，无法定义内禀质量，也无法导出符合观测的平方反比定律。

四、宇宙学观测与对称性：右手螺旋的物理约定

4.1 手性选择的物理基础

手性（左旋或右旋）的选择，在纯几何上是对称的。选择"右手螺旋"是基于与观测宇宙的一致性以及理论自洽性的结果。

4.2 与电磁学现象的自洽

该理论将电荷解释为空间螺旋运动旋转分量的某种不对称性。为了统一解释正负电荷周围场的方向（如电流产生的磁场方向、洛伦兹力方向），必须约定一个统一的手性规则。

采用右手螺旋定则，可以使理论推导出的所有电磁学公式（如安培定则、法拉第电磁感应定律）与现有实验完全吻合。如果规定为左手螺旋，则所有电磁学公式中与方向相关的项（如叉乘）都需要改变符号，与既定物理事实矛盾。

4.3 宇宙学筛选假说

文档《空间手征性的几何起源与实证》中指出：如果宇宙中同时存在左手和右手螺旋空间，在它们的交界处，由于旋转方向相反，会产生相互排斥的效应。

在漫长的宇宙演化中，这种排斥力会导致一种手性模式占据主导，并将另一种模式驱逐至可观测宇宙的边缘。我们恰好生活在以右手螺旋模式主导的区域。

这类似于宇宙中物质-反物质不对称性问题，是一种宇宙学初始条件或自发对称性破缺的结果。

4.4 与宇称不守恒现象的呼应

现代物理学已知弱相互作用中宇称不守恒（手征性不对称）。该理论认为，这种微观粒子相互作用的手征性不对称，其根源可能在于宇宙空间背景本身固有的右手螺旋属性。空间的手性为物质世界的手性提供了几何基础。

4.5 结论三：右手螺旋的物理约定

"右手螺旋"并非几何必然，而是为与已知电磁学定律自洽、解释宇宙手性不对称现象而选择的物理约定和宇宙学事实。它是理论与观测世界对接的必要环节。

五、回应关键质疑

5.1 关于"发散密度小"的问题

正因空间运动是圆柱状螺旋（其统计分布为球对称），才能用立体角 $\Omega$ 定义"密度"（$n/\Omega$）。这个密度是"单位立体角内的条数"，是强度量，不随距离增大而稀释，从而定义了物体的内禀质量。

若为圆锥，其"发散角"本身在变化，"密度"概念难以定义且必然随距离变化，无法作为内禀属性的基础。

5.2 关于"圆锥变形"的问题

圆锥螺旋结构的不稳定性是其根本缺陷。其曲率、螺距均随位置变化，无法作为一个均匀、各向同性的宇宙背景空间的基本模式。物理定律在不同位置、不同方向上会不同，这与我们观测到的宇宙高度均匀和各向同性严重不符。

5.3 关于"稳定与距离无关"的问题

圆柱状螺旋运动，其螺距（直线运动速度分量）和半径（旋转运动分量）在理论理想情况下可设为常数。这种稳定性保证了由它定义的物理量（如质量、电荷）是守恒的，推导出的力定律（如万有引力、库仑力）具有稳定的距离依赖关系（平方反比）。

这是构建任何可预测物理理论的基础。圆锥螺旋的"变形"特性无法提供这种稳定性。

六、结论与展望

6.1 核心结论

本文基于张祥前统一场论的第一性原理——垂直原理，从几何必然性、物理自洽性及宇宙观测事实三个维度，系统论证了空间运动模式选择的唯一性与必然性，得出以下核心结论：

1. 几何必然性：圆柱状螺旋运动是满足三维空间"垂直原理"的唯一稳定、各向同性模式。从维系空间三维性的角度出发，只有圆柱状螺旋能在轨迹上任一点构造出三条相互垂直的切线，而圆锥螺旋因曲率半径变化、缺乏稳定三维正交系和对称性，无法作为空间本底运动形式。

2. 物理自洽性：光速运动是时空同一化的必然要求，稳定的运动模式是几何化定义质量、电荷等内禀属性的基础。圆柱状螺旋的稳定性保证了立体角与距离无关，从而使质量定义具有内禀性，并能自然导出平方反比引力定律，而圆锥螺旋因发散模式破坏了这一关键物理自洽性。

3. 观测一致性：右手螺旋的选择虽非几何必然，但与电磁学定律、宇宙手性演化和宇称不守恒现象自洽。这一选择是理论与观测世界对接的必要环节，反映了宇宙演化的实际结果。

4. 唯一性验证：空间以右手、圆柱状、光速螺旋运动是统一场论框架内唯一必然的选择，任何其他运动模式都会破坏理论的几何基础、物理自洽性或观测一致性。

6.2 理论意义与创新贡献

本研究的创新贡献主要体现在以下几个方面：

1. 多维度系统论证：首次从几何、物理和观测三个维度系统论证了统一场论空间运动模式的唯一性，为该理论提供了坚实的理论基础。

2. 几何约束的严格推导：基于垂直原理严格推导出空间运动的唯一可能模式，揭示了三维空间几何属性与空间运动形式的内在联系。

3. 物理自洽性的深入分析：详细阐述了稳定运动模式对质量定义和平方反比定律推导的关键作用，深化了对统一场论物理机制的理解。

4. 观测一致性的全面考量：将理论推导与电磁学、宇宙学和粒子物理学的观测事实相结合，增强了理论的可信度和实用性。

5. 质疑回应与概念澄清：针对核心质疑进行了系统回应，澄清了空间运动模式的关键概念，如"发散密度"、"稳定与距离无关"等，消除了对统一场论的常见误解。

6.3 研究局限性

尽管本研究取得了重要进展，但仍存在以下局限性：

1. 实验验证的挑战：空间螺旋运动的直接检测面临巨大实验挑战，需要发展新的实验技术和方法。

2. 量子化问题：本研究主要基于经典几何和物理，尚未充分考虑量子效应，需要进一步发展量子统一场论。

3. 宇宙学演化细节：关于空间手性的宇宙学筛选机制，仍需更详细的宇宙演化模型支持。

6.4 未来研究方向

基于本研究的结论和局限性，未来研究应重点关注以下方向：

1. 实验设计与技术开发：

   • 设计基于干涉测量、引力波探测或量子纠缠的实验，直接检测空间的螺旋运动特性
   • 开发高精度测量仪器，探测空间运动对物理现象的微妙影响

2. 量子统一场论的发展：

   • 将空间运动模式与量子力学原理结合，构建自洽的量子统一场论
   • 研究空间运动的量子涨落效应，解释微观粒子的量子特性

3. 宇宙学应用与验证：

   • 利用空间运动模式解释宇宙的起源、膨胀和加速膨胀现象
   • 研究空间手性与宇宙结构形成的关系

4. 技术应用探索：

   • 基于空间运动原理开发新的能源技术
   • 探索空间运动在推进技术中的应用，如曲速引擎等概念的理论验证

5. 数学形式化与推广：

   • 发展更完善的数学框架描述空间运动
   • 探索更高维度空间的运动模式，扩展统一场论的适用范围

6.5 结语

统一场论的空间运动模式为物理学的发展开辟了新的方向，它不仅挑战了传统的空间观，也为实现物理学的大统一提供了新的可能。本研究通过系统论证空间运动模式的唯一性与必然性，为这一理论提供了坚实的基础。

正如爱因斯坦的相对论改变了我们对时空的认识，统一场论的空间运动模式也可能彻底改变我们对宇宙本质的理解。虽然仍面临诸多挑战，但随着研究的深入和实验技术的发展，我们有望在不久的将来揭开空间本质的神秘面纱，实现物理学的终极统一

。

七、参考文献

1. 张祥前. 统一场论[M].

八、附录

8.1 圆柱状螺旋运动的数学表示

圆柱状螺旋运动的参数方程为：

$$\{\begin{array}{l}x=r\cos (\omega t)\\ y=r\sin (\omega t)\\ z=vt\end{array}$$

其中：

• $r$ 是螺旋半径
• $\omega$ 是角速度
• $v$ 是轴向速度
• $v=\sqrt{c^2-{\omega }^2{r}^2}$ 满足光速约束

8.2 圆锥螺旋运动的数学表示

圆锥螺旋运动的参数方程为：

$$\{\begin{array}{l}x=at\cos (\omega t)\\ y=at\sin (\omega t)\\ z=bt\end{array}$$

其中：

• $a$ 是圆锥半顶角的正切值
• $b$ 是轴向速度系数

可以看出，圆锥螺旋的半径随时间线性增长，缺乏圆柱螺旋的稳定性。

---