Python求解微分方程，详细版（部分含Matlab）

一、什么是微分方程

（一）什么是微分方程

微分方程（differential equation）：表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。

（二）微分方程分类

        如果自变量的个数只有一个，称为常微分方程（Ordinary differential equation，ODE）；如果自变量的个数不止一个，称为偏微分方程（Partial differential equation，PDE）。

        线性微分方程（Linear differential equation）：若未知函数与其导数（偏导数）是一次有理整式，则称该微分方程是线性的。

        微分方程组：用两个及以上的关系式表示的微分方程称为微分方程组。

1、常微分方程

一般 n 阶常微分方程具有如下形式：

而 n 阶线性常微分方程具有如下形式：

在牛顿力学中，位移，速度，时间三者之间的关系就是最简单的一阶线性常微分方程：

 d x / d t = v ( t )

其中自变量是t，未知函数是x，未知函数的导数是 v 。再比如传染病模型，是一阶非线性常微分方程：

d x / d t=k*x*(n-x)

其中自变量是t表示某一时刻；x 是未知函数，表示t时刻染病人数；k是传染系数；n是该地区总人数。

常见常微分方程的表达式表示如下：

令那么 n 阶常微分方程可用一阶方程组代替：

2、偏微分方程

设Ω是 Rⁿ中的一个集合， x =(x1,x2,…, xn）表示Ω上的一点。

 u = u ( x ):Ω→ R表示一个 n元函数。记：

其中，(i1, i2 ,…, ik）是集合｛1,2,…, n ｝中k个元素的任意排列。那么一般的

k阶偏微分方程具有如下形式：

k 阶线性偏微分方程具有如下形式：

其中

和 f 是给定函数；表示多重指标：

其中，和 f 是给定函数。

下面是一些经典的微分方程：

拉普拉斯方程（ Laplace equation ）是最经典的二阶线性偏微分方程：

拉普拉斯方程也称为调和方程（ Harmonic equation )。调和方程的解称为调和函数( Harmonic function )。

另外，还有三个典型的二阶线性偏微分方程：

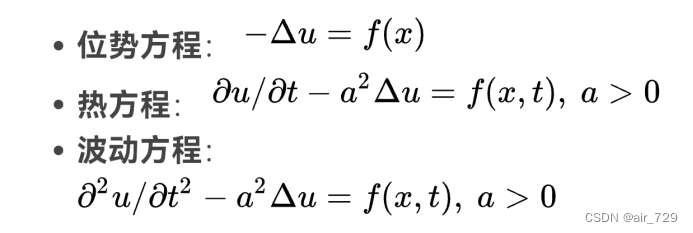
在 Rm中，二阶线性偏微分方程的一般形式为：

其中：  

（三）微分方程求解步骤

1、确定微分方程的类型

微分方程可以分为常微分方程和偏微分方程两大类。在解微分方程之前，需要先确定方程的类型，以便选择合适的方法进行求解。

2、确定微分方程的阶数

微分方程的阶数是指未知函数的最高阶导数的阶数。根据微分方程的阶数，可以选择不同的解法。常见的微分方程阶数有一阶、二阶和高阶微分方程。

3、将微分方程转化为标准形式

将微分方程转化为标准形式是解微分方程的关键一步。标准形式可以简化微分方程的求解过程，使问题更清晰明了。转化的方法包括变量代换、换元法、特殊函数等。

4、求解微分方程

根据微分方程的类型和阶数，选择合适的求解方法。常见的求解方法包括分离变量法、齐次方程法、线性方程法、变量替换法、级数展开法等。

5、验证解的正确性

解得微分方程后，需要对解进行验证，确保解符合原微分方程。验证的方法可以通过将解代入原方程，检验等式是否成立，或者对解进行导数运算，验证导数是否满足原方程。

6、给出特解或通解

根据微分方程的边界条件和初始条件，确定特解或通解。特解是满足特定条件的解，而通解是包含所有特解的解集。通过给定的条件，可以求解出特解或确定通解的形式。

7、可视化分析

在解的方程后，可进行可视化分析，将解表达为函数图像或曲线。通过可视化分析，可以更直观的理解微分方程的意义和解的特性。

二、用python语言求解微分方程的办法

（一）一阶微分方程

1、一阶线性微分方程（python和Matlab）

例如：

对一阶线性微分方程g’(x)-g(x)=0求其通解以及当x=0时，g(x)=1的特解

求解代码如下：

pprint()输出结果如下：

print()输出结果如下：

一阶微分方程绘图：

对一阶微分方程：g’(x)-g(x)=0

初值条件为：g(x)=1；

绘图代码及结果如下：

Matlab写法：一阶线性微分方程g’(x)-g(x)=0通解以及当x=0时，g(x)=1的特解

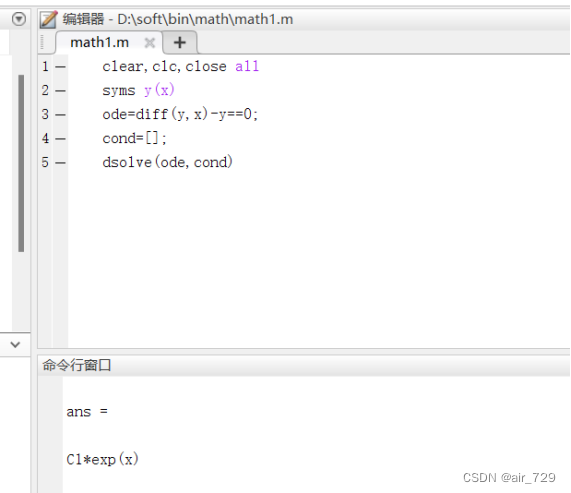
特解：

用Matlab写了这一点是因为这学期选了一个科学计数法的网课选修课，它里边讲Matlab，所以对它有一点接触，但不多，刚好提到可以用这个写作业，有点好奇，所以就在网上找了破解版下载了，目前只会求解一阶微分方程和简单的二阶微分方程，还不会画图。解析式求解如下图：

对二阶微分方程y ’’- y =0求解：

2.一阶非线性微分方程

例如：

对一阶非线性微分方程g’(x)-g(x)²=0求其通解以及当x=0时，g(x)=-1的特解。代码如下：

pprint()输出：

print()输出：

（二）二阶微分方程

例如：g’’(x)-2g’(x)+g(x)-sin x =0

初值条件：g(0)=1, g(1)=2；

求其通解和特解代码如下：

print()输出：

二阶微分方程绘图：

二阶方程，需要化成两个一阶方程组成的方程组，把每个得到的方程组化成y’= f ( x , y ) 形式，这里的x和y是相对每个方程而言的，因为要求的是数值解，所以需要确定好参数值和初始条件，在odeint中默认输入y = 0时因变量的值；确定自变量范围并解方程，绘制图像。

解微分方程：y’’(t) - b*y’(t) + y(t) - sin t=0，其中b为参数, 令b=2，先化成两个一阶微分方程，如下图所示：

代码如下：

图形如下：

（三）高阶微分方程

例如：

四解微分方程g’’’’(x)-2g’’’(x)+5g’’(x)=0

初值条件：

g(0)=1,  g(1)=2,  g(2)=3,  g(3)=4

print()输出:

如有错误，望大家批评指正！感激不尽！