Python—微分方程

Python_魔力猿

于 2023-08-22 11:02:07 发布

阅读量935

点赞数

文章标签： python 开发语言

本文链接：https://blog.csdn.net/weixin_68789096/article/details/132423629

版权

结合Python中Scipy，专注创建可以解决问题的方程

目录

一阶常微分方程

二阶常微分方程

三阶常系数微分方程组

修正贝塞尔微分方程

伯努利方程

一阶常微分方程

加速度、速度、时间

计算物体速度的时候，若加速度不断变化，如何确定速度和时间的关系？假设加速度随速度和时间变化的关系是：

即：

我们利用Scipy求解该方程：

import numpy as np   import matplotlib.pyplot as plt      from scipy.integrate import odeint      # v是速度，t是时间   def dvdt(v, t):       return v + 6*t      v0 = 0   t = np.linspace(0, 2, 100)      # 结果res是 N行1列的二维数组（因为是一元方程）   res = odeint(dvdt, v0, t)      # 转置之后第一行就是各个时间点的速度   res_v = res.T[0]      # 绘制速度和时间的关系   plt.plot(t, res_v)   plt.show()

由下图结果易得加速度随时间逐渐增大。

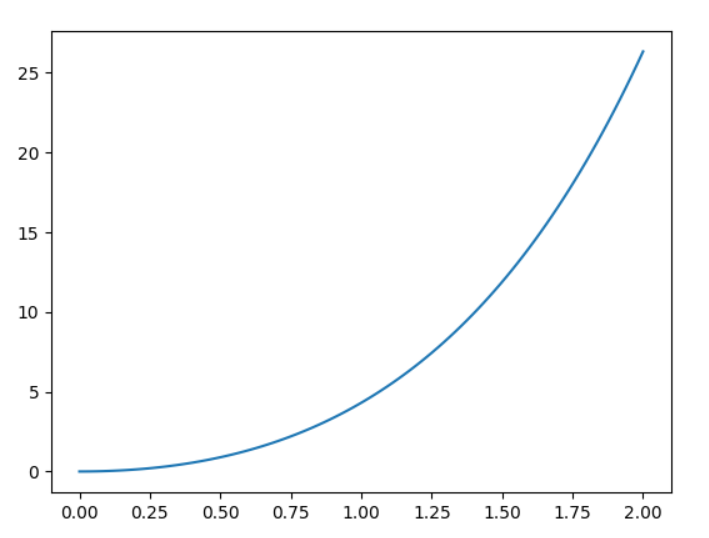
图1

二阶常微分方程

且

，，

# 二阶ODE的求解   import matplotlib.pyplot as plt   import numpy as np   from scipy.integrate import odeint         def dSdx(x, S):       x, v = S       return [v, -v ** 2 + np.sin(x)]         x_0 = 0   v_0 = 3   S_0 = (x_0, v_0)   t = np.linspace(0, 1, 100)   sol = odeint(dSdx, y0=S_0, t=t, tfirst=True)   x_sol = sol.T[0]   v_sol = sol.T[1]   l1, = plt.plot(t, x_sol)   l2, = plt.plot(t, v_sol)   plt.legend((l1, l2), ['x', 'v'])   plt.show()

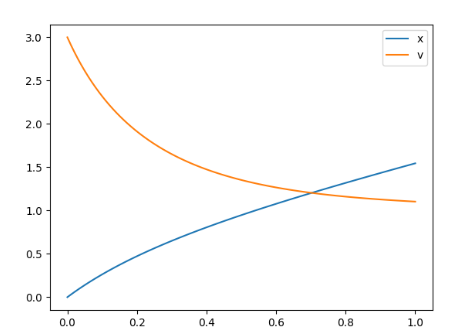
图2

这个二阶ODE描述了速度v相对于位置x的变化率。变量S是一个元组(x, v)，它表示系统在给定点(x, v)的状态。通过使用龙格-库塔法或欧拉法等适当的方法对该系统进行数值求解，我们可以确定函数v(x)，它表示速度作为位置的函数。

三阶常系数微分方程组

对于该方程组：

利用Scipy求解编程如下：

# 将三阶常系数微分方程组x‘’‘=-x1’‘^3+x2'+x1+sin(t)和x1'''=-2x2'^2+x2   # 对于上式，这里定义新变量v1、v2和a1、a2,并将方程组向量化可以得到      import matplotlib.pyplot as plt   import numpy as np   from scipy.integrate import odeint         def dSdt(t, S):       x1, v1, a1, x2, v2, a2 = S       return [v1,               a1,               -2 * v2 ** 2 + x2,               v2,               a2,               -a1 ** 3 + v2 + v1 + np.sin(t)]         x1_0 = 0   v1_0 = 0   a1_0 = 0   x2_0 = 0   v2_0 = 0   a2_0 = 0   v_0 = 0   S_0 = (x1_0, v1_0, a1_0, x1_0, v1_0, a1_0)   t = np.linspace(0, 1, 100)   sol = odeint(dSdt, y0=S_0, t=t, tfirst=True)   plt.subplot(1, 2, 1)   l1, = plt.plot(t, sol.T[0], 'r')   plt.title('x1')   plt.subplot(1, 2, 2)   l2, = plt.plot(t, sol.T[3], 'b')   plt.title('x2')   plt.show()

图3

修正贝塞尔微分方程

贝塞尔方程是齐次线性二阶变系数方程：

其解称为贝塞尔函数，该函数数学物理中具有重要作用。由表示其中的一个解并称之为阶贝塞尔函数。幂级数展开后如下，当和时：

import numpy as np   import matplotlib.pyplot as plt   from scipy.special import jv   from scipy.integrate import odeint         def bessel_equation(y, x):       return [y[1], -y[1] / x - ((x ** 2 - n ** 2) * y[0]) / x ** 2]         x = np.linspace(0.1, 10, 100)  # Define the range of the independent variable x   n = 2  # Bessel equation parameter n   y0 = [jv(n, x[0]), jv(n, x[0]) / x[0]]  # Define the initial conditions using Bessel functions      # Use odeint function for numerical solution   sol = odeint(bessel_equation, y0, x)      # Extract the first component of the solution, i.e., y(x)   y = sol[:, 0]      # Plot the solution curve   plt.plot(x, y)   plt.xlabel('x')   plt.ylabel('y(x)')   plt.title('Solution of the Modified Bessel Equation')   plt.grid(True)   plt.show()

选择n=2作为贝塞尔方程的参数，绘制该参数下的解曲线：

图4

伯努利方程

其中(和) 被称作伯努利方程，它是一个非线性微分方程，可以通过降阶为一个线性微分方程并可以通过求积分得其解。例如该方程：

import numpy as np   import matplotlib.pyplot as plt   from scipy.integrate import odeint         def bernoulli_equation(y, x):       return y[1], x * y[1] - y[0] + x ** 2         x = np.linspace(0, 5, 100)  # 定义自变量 x 的范围   y0 = [1, 0]  # 定义初始条件，这里假设 y(0) = 1，y'(0) = 0      # 使用 odeint 函数进行数值求解   sol = odeint(bernoulli_equation, y0, x)      # 提取解的第一个分量，即 y(x)   y = sol[:, 0]      # 绘制解的曲线   plt.plot(x, y)   plt.xlabel('x')   plt.ylabel('y(x)')   plt.title('Solution of the Bernoulli Equation')   plt.grid(True)   plt.show()

图5

当然可以根据不同需求调整自变量的范围和初始条件：

import numpy as np   import matplotlib.pyplot as plt   from scipy.integrate import odeint         def bernoulli_equation(y, x):       return y[1], x * y[1] - y[0] + x ** 2         x = np.linspace(0, 1, 1000)  # 定义自变量 x 的范围   y0 = [1, 0]  # 定义初始条件，这里假设 y(0) = 1，y'(0) = 0      # 使用 odeint 函数进行数值求解   sol = odeint(bernoulli_equation, y0, x)      # 提取解的第一个分量，即 y(x)   y = sol[:, 0]      # 绘制解的曲线   plt.plot(x, y)   plt.xlabel('x')   plt.ylabel('y(x)')   plt.title('Solution of the Bernoulli Equation')   plt.grid(True)   plt.show()