信号处理之压缩感知理论

1. 压缩感知-发展背景

在21世纪初，由美国的Donoho和Candes等人提出了一种全兴的理论，即压缩感知理论（Compressed Sensing）。该理论指出只要信号是可压缩或者在某个变换域是稀疏的，那么就可以以远低于奈奎斯特频率的采样率获取稀疏信号的非自适应线性投影，然后通过最优化问题可以从有限的采样值中精确重构原信号。该理论建立了一个新的信号描述和处理的理论框架，突破了奈奎斯特采样频率的限制，对信息科学领域的意义十分重大。

压缩感知的前提要求信号是可压缩的或者在某个变换域是稀疏的，然后利用一个与变换基不相关的观测矩阵对信号进行投影，最后通过求解优化问题重构原信号。显然这个理论在采样的同时也实现了信号的压缩，它其实是一个对信号携带信息进行采样的过程。从这个过程中我们容易看出压缩感知理论主要涉及以下几个方面的内容：

（1）信号的稀疏表示，即找到一个基，使得信号在这个基的表示下具有良好的稀疏性；    

（2）信号的观测矩阵的设计，设计一个平稳的与变换基不相关的观测矩阵，使得信号携带信息免遭破坏，实现低速采样；

（3）信号重构，即从较少的观测数据中根据过完备原子字典恢复重构出原来信号。

这几个方面便是压缩感知理论的核心部分。

2. 理论框架-传统压缩采样

在传统的采样与压缩过程中，首先对信号进行满足奈奎斯特的采样，然后对得到的采样值进行转换，再对转换后的信号压缩（如傅里叶变换等），得到变换压缩的信号。恢复信号的过程只要对信号进行解压缩然后进行与前面相反的反变换就能得到原始信号。由于这个过程是在高速采样后再进行变换压缩，所以难免丢弃了大量的采样值，造成了数据计算和内存资源的浪费。

3. 理论框架-压缩感知

压缩感知理论作为一种新的理论框架，它对信号的采样和压缩发生在同一个步骤，下图是压缩感知的理论框架。从图中我们可以清楚的看到压缩感知涉及三部分内容，首先，前提条件是信号必须是稀疏的或者可压缩的，这是信号稀疏表示的先验条件，然后通过选择稳定的测量矩阵，这个矩阵必须满足RIP性质（有限等距性质Restricted Isometry Property）的约束，通过测量矩阵对原始信号进行线性投影得到投影测量值；最后通过优化问题重构原来的信号    

其中

稀疏性是压缩感知的前提。关于稀疏的定义如下，

  对于长度为N的向量（实际上是指一个N维离散信号）来说，它的N个元素值只有K个是非零的，其中K<<N，这时我们称这个向量是K稀疏的或者说是严格K稀疏的；实际中要做到严格K稀疏不容易，一般来说，只要除了这K个值其它的值很小很小，我们就认为向量是稀疏的，这时区别于严格K稀疏且就叫它K稀疏吧

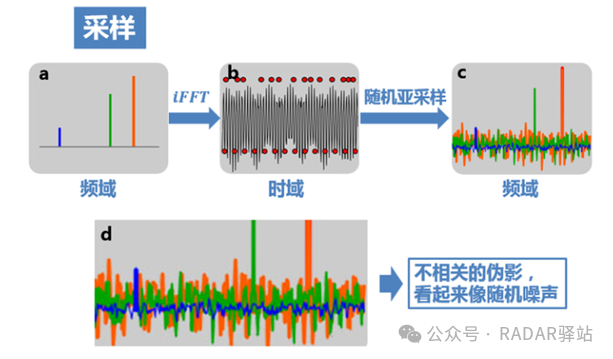
4.理论框架-采样与恢复

如果采用随机亚采样（图b上方的红点），那么这时候频域就不再是以固定周期进行延拓了，而是会产生大量不相关（incoherent）的干扰值。如图c，最大的几个峰值还依稀可见，只是一定程度上被干扰值覆盖。这些干扰值看上去非常像随机噪声，但实际上是由于三个原始信号的非零值发生能量泄露导致的（不同颜色的干扰值表示它们分别是由于对应颜色的原始信号的非零值泄露导致的）。可以理解成随机采样使得频谱不再是整齐地搬移，而是一小部分一小部分胡乱地搬移，频率泄露均匀地分布在整个频域，因而泄漏值都比较小，从而有了恢复的可能。    

(1) 由于原信号的频率非零值在亚采样后的频域中依然保留较大的值，其中较大的两个可以通过设置阈值，检测出来（图a）。

(2) 然后，假设信号只存在这两个非零值（图b），则可以计算出由这两个非零值引起的干扰（图c）。

(3) 用a减去c，即可得到仅由蓝色非零值和由它导致的干扰值(图d），再设置阈值即可检测出它，得到最终复原频域（图e）

(4) 如果原信号频域中有更多的非零值，则可通过迭代将其一一解出。

5.稀疏分解-正交变换基下的稀疏表示    

       根据上边的描述，对于原始信号的稀疏表示，关键在于正交稀疏基的选择，信号的稀疏表示就是将信号投影到正交变换基时，绝大部分变换系数的绝对值很小，所得到的变换向量是稀疏或者近似稀疏的，常用的有离散余弦变换基、快速傅里叶变换基、离散小波变换基、冗余字典等。

用正交基稀疏表达一个信号也有很多缺点，因为一组基表达信号的能力取决于信号的特征是否与基向量的特征相吻合；例如，光滑连续信号可以被傅里叶基稀疏的表达，但脉冲信号就不行。现实世界中的信号经常包含有用单一基所不能表达的特征。对于这些信号，你或许希望可以选择来自不同基的向量（如用小波基和傅里叶基来联合表达一个信号）。因为你想保证你可以表达一个信号空间的所有信号向量，所以由所有可选向量组成的字典应该能够张成这个信号空间。然而由于这组字典中的向量来自不同的基，它们可能不是线性独立的。由于这组字典中的向量不是线性独立的，会造成用这组字典做信号表达时系数不唯一。然而如果创建一组冗余字典，你就可以把你的信号展开在一组可以适应各种时频或时间-尺度特性的向量上。这样构造的字典可以极大地增加你稀疏表达各种特性信号的能力。

6. 稀疏分解-冗余字典下的稀疏表示

         最近几年，对稀疏表示研究一个热点是信号在冗余字典下的稀疏分解，这是一种全新的信号表示理论，它用超完备的冗余函数取代基函数。定义表达你的信号空间的归一化基本模块作为字典。这些归一化向量叫做原子。如果字典的原子张成了整个信号空间，那么字典就是完全的。如果有原子之间线性相关，那么字典就是冗余的。在大多数匹配追踪的应用中，字典都是完全且冗余的。以匹配追踪算法（Matching Pursuit，MP）为例，实现过程如下。    

          

          

7. 观测矩阵（测量矩阵）

         在基础理论框架中，我们知道，当可压缩信号经过稀疏变换得到稀疏表示后，需要经过一个观测矩阵，使得在这个观测矩阵上的投影得到的观测值能够表示原始信号的大部分信息，这样才能保证信号的精确重构。观测的过程实际上是稀疏信号与观测矩阵的内积过程，得到M个观测值。

    

        在上面的采样过程中，Φ是固定的，它不依赖于信号x。如果给定y依据上式重构x，由于M<<N,方程的个数少于未知数的个数，这是一个求解欠定方程的问题，无法得到准确的解，因此无法重构信号，但因为原始信号是K-稀疏的，如果给定下面的约束条件，即有限等距性质（Restricted Isometry Property,RIP）,就能构重构出原始信号。其中，ε为一很小的大于0的常数。

需要特别注意的是，实际上RIP是针对传感矩阵A的。由于稀疏矩阵是固定的，要使得传感矩阵满足约束等距条件，可以通过设计测量矩阵解决。因此网上的资料大多都是对测量矩阵提出满足RIP条件来设计的。

8. 观测矩阵-有限等距性质

陶哲轩和Candès证明了RIP才是观测矩阵要满足的准确要求。但是，要确认一个矩阵是否满足RIP非常复杂。于是Baraniuk证明：RIP的等价条件是观测矩阵和稀疏表示基不相关（incoherent）。这就是压缩感知的第二个前提条件。    

那怎样找到不相关的观测矩阵呢？陶哲轩和Candès又证明：独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。于是满足高斯分布的随机测量矩阵就成了压缩感知最常用的观测矩阵。对于二维信号，往往就采用如左图所示的采样矩阵对图像进行亚采样。对于一维信号，采用前文提到的随机不等间距的亚采样即可。

9. 稀疏重构-分解与重构

压缩感知中的信号重构是理论的核心部分，前部分说到，信号重构的过程是一个约束于RIP性

质下求解欠定方程的过程，与稀疏分解相比，他们的区别如下

       1）稀疏分解要解决的问题是在冗余字典A中选出k列，用这k列的线性组合近似表达待稀疏分解信号y，可以用表示为y=Aθ，求θ。

       2）压缩感知重构要解决的问题是事先存在一个θ和矩阵A，然后得到y=Aθ（压缩观测），现在是在已知y和A的情况下要重构θ。

        实际上它们要解决的问题都是对已知y和A的情况下求y=Aθ中的θ。

        上面各式中，A为M×N矩阵（M<<N，稀疏分解中为冗余字典，压缩感知中为传感矩阵A=ΦΨ，即测量矩阵Φ乘以稀疏矩阵Ψ），y为M×1的列向量（稀疏分解中为待稀疏分解信号，压缩感知中为观测向量），θ为N×1的列向量（稀疏分解中为待求分解系数，压缩感知中为信号x的在变换域Ψ的系数，x=Ψθ）。

       所不同的是，在稀疏分解中θ是事先不存在的，我们要去求一个θ用Aθ近似表示y，求出的θ并不能说对与错；在压缩感知中，θ是事先存在的，只是现在不知道，我们要通过某种方法如OMP（正交匹配追踪）去把θ求出来，求出的θ应该等于原先的θ的，然后可求原信号x=Ψθ。

。

10. 稀疏重构-最小范数问题

0范数或1范数最优化总会导致一个稀疏解，而转化为2范数最优化求得的解存在一定的偏差，因此重构一般采用L1范数最优化来解。

11. 稀疏重构-正交匹配追踪（OMP算法）

采用L1范数最优化的正交匹配追踪算法（OMP）流程如下：    

12. 稀疏重构-OMP仿真代码

clc;clear

%%  1. 时域测试信号生成

K=7;      %  稀疏度(做FFT可以看出来)

N=256;    %  信号长度

M=64;     %  测量数(M>=K*log(N/K),至少40,但有出错的概率)

f1=50;    %  信号频率1

f2=100;   %  信号频率2

f3=200;   %  信号频率3

f4=400;   %  信号频率4

fs=800;   %  采样频率

ts=1/fs;  %  采样间隔

Ts=1:N;   %  采样序列

x=0.3*cos(2*pi*f1*Ts*ts)+0.6*cos(2*pi*f2*Ts*ts)+0.1*cos(2*pi*f3*Ts*ts)+0.9*cos(2*pi*f4*Ts*ts);  %  完整信号

%%  2.  时域信号压缩传感

Phi=randn(M,N);                                   %  测量矩阵(高斯分布白噪声)

s=Phi*x.';                                        %  获得线性测量

%%  3.  正交匹配追踪法重构信号(本质上是L_1范数最优化问题)

m=2*K;                                            %  算法迭代次数(m>=K)

Psi=fft(eye(N,N))/sqrt(N);                        %  傅里叶正变换矩阵

T=Phi*Psi';                                       %  恢复矩阵(测量矩阵*正交反变换矩阵)

hat_y=zeros(1,N);                                 %  待重构的谱域(变换域)向量                    

Aug_t=[];                                         %  增量矩阵(初始值为空矩阵)

r_n=s;                                            %  残差值

for times=1:m;                                    %  迭代次数(有噪声的情况下,该迭代次数为K)

    for col=1:N;                                  %  恢复矩阵的所有列向量    

        product(col)=abs(T(:,col)'*r_n);          %  恢复矩阵的列向量和残差的投影系数(内积值) 

    end

    [val,pos]=max(product);                       %  最大投影系数对应的位置

    Aug_t=[Aug_t,T(:,pos)];                       %  矩阵扩充

    T(:,pos)=zeros(M,1);                          %  选中的列置零（实质上应该去掉，为了简单我把它置零）

    aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s;           %  最小二乘,使残差最小

    r_n=s-Aug_t*aug_y;                            %  残差

    pos_array(times)=pos;                         %  纪录最大投影系数的位置

end

hat_y(pos_array)=aug_y;                           %  重构的谱域向量

hat_x=real(Psi'*hat_y.');                         %  做逆傅里叶变换重构得到时域信号

%%  4.  恢复信号和原始信号对比

figure(1);

hold on;

plot(hat_x,'k.-')                                 %  重建信号

plot(x,'r')                                       %  原始信号

legend('Recovery','Original')

norm(hat_x.'-x)/norm(x)                           %  重构误差

仿真结果： 

 更多内容，可关注微信公众号：RADAR驿站