研究了均匀扭转和非均匀扭转的理论。本文的目的是研究不同截面梁在不同载荷和支撑条件下的组合弯曲和扭转行为。利用ANSYS 18.1工作台,对不同几何截面的实心和空心圆形截面、矩形截面和对称I截面梁在简支和悬臂端部条件下承受同心和偏心加载条件下的有限元进行了比较研究。梁的长度保持恒定为 4 m。研究了梁的横向和轴向变形、等效应力和应变以及破坏模式和弯曲和扭转的影响。据观察,同心载荷导致横向偏转,而扭转力矩载荷以横截面扭曲的形式引起面内变形,产生最大应力,偏心载荷导致横向和面内轴向变形的组合。从获得的结果可以说,与空心圆形和矩形截面相比,开放截面对于扭转和偏心类型负载的效率较低,因为观察到更高的应力和轴向挠度。

本文由Google翻译,原文PDF下载链接:
https://pan.baidu.com/s/1Jf_YSN-wY13EU2tmIizrFg
提取码:du5u
Introduction
1 Introduction介绍
梁是任何结构中最基本的结构元素。在当今的建筑领域,钢梁主要用于复合结构。钢构件因其强度特性、延展性、灵活性和成本效益而被广泛用作高层建筑、桥梁、住宅棚、工业棚、停车场等的结构元件。钢筋是建筑施工中使用的常见形式,可以具有各种形状,如圆形、矩形和方形[1]、[2]、[3]。板元件用作屋顶覆盖物,钢平板通常用于栏杆、格栅工程和建筑部分。钢构件的特性主要取决于构件的几何形状和强度特性。通过分析结构构件在不同荷载条件下的行为来选择合适的截面对于使结构安全、经济是非常重要的。人们采用了实验研究和数值方法等多种方法来研究此类成员的行为。这些方法给出了现实生活中的响应,但耗时、乏味且成本高昂[4]、[5]。已经开发了多种分析方法来分析梁结构。有限元法是近年来广泛应用的方法之一[14] . 可以通过有限元方法分析结构元件在不同支撑条件下的各种载荷下的行为,并获得所产生的应力、应变、挠度和位移。ANSYS Workbench 应用程序是基于有限元方法的计算机应用程序[6]、 [9]。在钢结构中,纯扭转不会单独发生。大多数时候,扭转是与弯曲效应相结合而发生的。因此,根据扭转效应是直接传递载荷还是由于其他效应而分别产生,扭转效应可以分为初级扭转和次级扭转[8]、 [10]。
常用的I型材通常能有效地抵抗弯曲作用,而空心型材和H型材则能有效地抵抗扭转。横截面由在公共点相交的圆形或薄矩形元素组成,并且旋转轴穿过截面的剪切中心,那么在这些截面中将不会由于扭转而产生翘曲效应 [11] 、[ 12 ]。
Anna Jaskot [7]根据 Huber Von Mises 假设,以数值方式和分析方式提出了梁偏转和最大折减应力。作者 Koken A 和 Kurt E [13]使用 ANSYS Workbench 程序提出了钢拉伸和压缩单元的解析解,计算了轴向拉伸和压缩载荷引起的应力和位移,并与理论结果进行了比较。将钢蜂窝梁三维非线性有限元分析结果与试验结果进行了比较。同样,Rushikesh Khartode 等人。[16]使用ANSYS对垂直静载荷条件下具有各种垂直和水平刚度条件的混合钢梁进行有限元分析。获得了不同加强筋位置的最大载荷行为和挠度的结果。N. Shanmugasundaram 和 Prince G. Arulraj [15]对 1 号发动机进行了参数研究。使用 ANSYS 15 设计具有不同几何截面的组合钢梁。研究了组合截面的弯矩和轴向力行为。兹德内克·卡拉[17]使用非线性有限元,包括初始轴曲率、材料特性、残余应力的影响,使用 ANSYS 软件提出了均匀力矩加载的真实工字梁的非弹性横向扭转屈曲阻力。在目前的工作中,我们尝试使用有限元分析软件包 ANSYS Workbench 18.1 对薄壁钢梁进行建模,并研究其行为和对各种类型载荷的影响。利用ANSYS软件对实心圆与矩形、空心圆与矩形、对称I截面不同几何截面梁在两端简支与悬臂不同支撑条件下同心与偏心条件下的有限元求解进行对比研究包裹。
Methodology
2 Methodology 方法
偏心轴承通常基于应具有高强度、可焊整个分析采用有限元分析软件ANSYS 18.1进行。根据支撑和载荷条件对梁进行建模,然后将横截面的属性分配给建模的梁。梁的长度保持恒定为4 m,如图1所示。所有部分的材料保持不变。如下所述考虑两个结束条件。考虑的梁端条件:
•悬臂梁
•简支梁
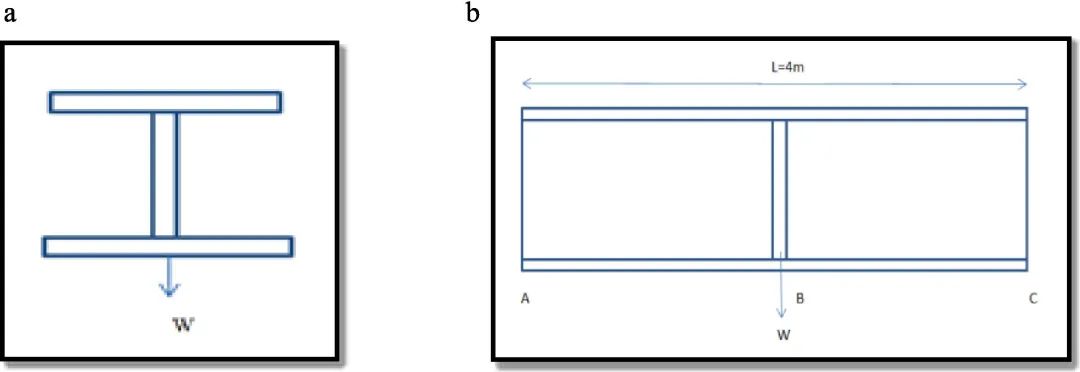
图1 . I截面(a)截面同心受力情况;(b) 剖面前视图
分析采用的加载条件是。
•点载荷(W)= 100 KN
•采用的部分安全系数 = 1.6(根据 BS 5950)
•因式点荷载 (Wu) = 100 × 1.6 = 160 KN
•偏心率 (e) = 75 mm(距 I 截面腹板中心)
•扭矩(Tq)=W×e=160×0.075=12KNm
偏心点载荷可以用同心载荷和绕截面的力矩(扭矩)来求解,如图2所示,可以容易地求解。
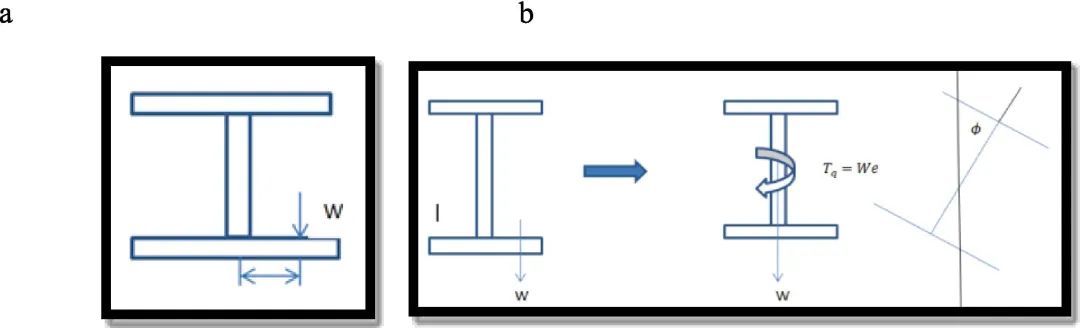
图2 . I 段偏载情况 (a) 偏载;(b) 偏心载荷的分辨率
Finite element analysis and calculation models
3 Finite element analysis and calculation models 有限元分析计算模型
使用ANSYS设计建模软件作为实体模型对24根梁进行建模,并使用ANSYS Workbench在静态结构模块中进行分析。有限元分析方法的基本流程如下:
•建模和元素类型
•材料特性
•网格划分
•载荷和边界条件
•结果和后处理
3.1 . 静态结构分析
静态结构分析(也称为静态分析)用于查找结构位移、应力、应变。在本研究中,所有具有特定尺寸、长度和载荷条件的梁均使用 ANSYS Workbench 18.1 有限元软件进行建模和分析,如图3所示。
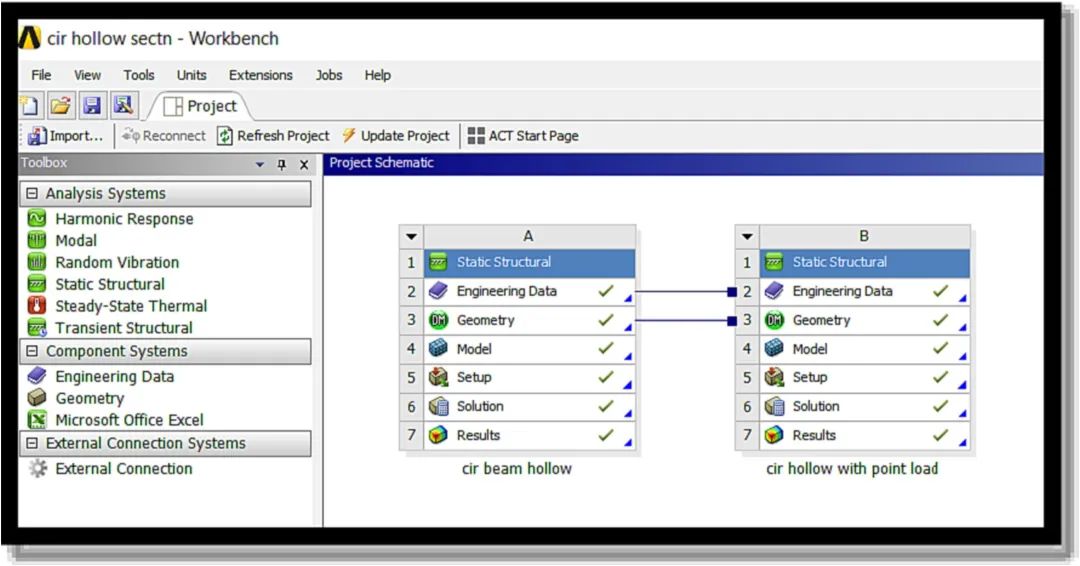
图3 . 静态结构分析简介
3.2 . 建模和元素类型
数学建模包括用户输入(例如几何数据)和开发结构模型。固体梁是使用程控梁元件开发的。材料属性按照 BS EN 19931-1:2005 指定。各种横截面的模型梁如图 4和图 5所示。所有问题的尺寸细节在下面的表1中描述,并且I型截面的一般横截面特性在下面的表2中。

图4 . 梁的模型视图 (a) 实心圆形;(b) 空心圆形;(c) 实心矩形
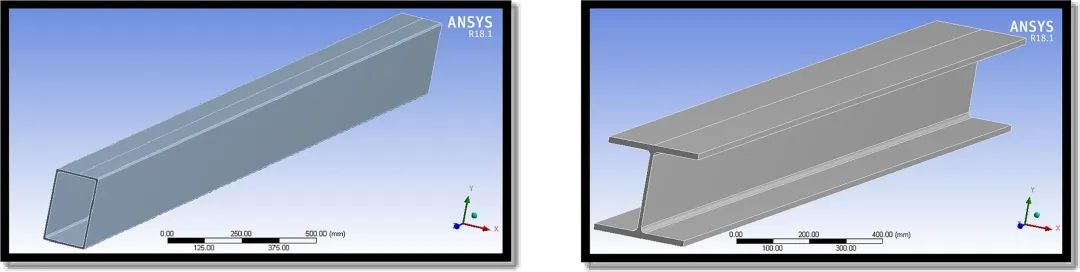
图5. 梁构件模型图 (a) 空心矩形;(b) I 部分

表 1 . 用于分析的横截面细节

表 2 . 对称I型截面的截面特征
3.3 . 材料特性
材料属性步骤包括将属性分配给所使用的模型。有限元模拟和数值分析考虑了根据 BS EN 1993-1-1: 2005 的热轧钢样本。材料特性值以 (MPa) 为单位,如下表 3所示,

表 3 . 建模梁截面的一般材料属性
3.4 . 网格划分
实体模型的网格划分保持圆形、矩形和对称 I 截面的每个单元的尺寸为 0.01 mm。图6、图7表示梁的网格模型。

图6 . 梁的网格模型视图 (a) 实心圆形;(b) 空心圆形;(c) 矩形
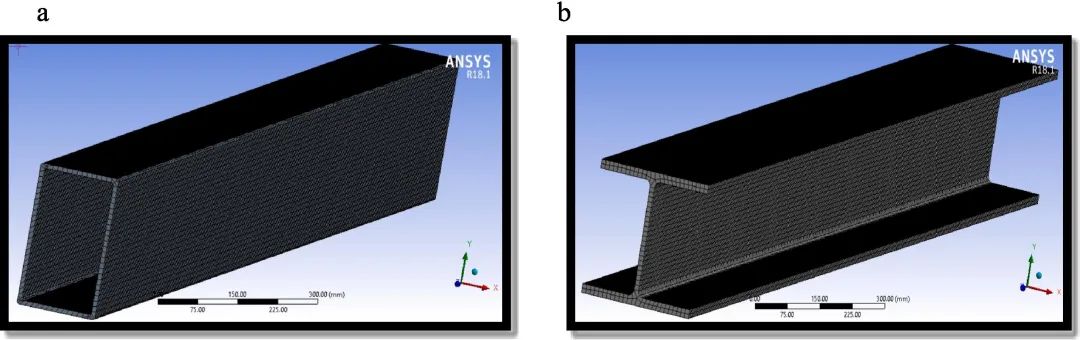
图7 . 梁的网格模型视图 (a) 空心矩形;(b) I型截面梁
3.5 . 载荷和边界条件
梁端的自由度要求定义了不同支撑建模的目的。作用在梁上的力必须根据问题解释来定义。用于进一步分析的所有梁的边界条件为:
•悬臂支撑条件
•简支条件
下表4描述了具有不同载荷条件和支撑条件的实心和空心圆形梁截面模型以及命名法,具有载荷和边界条件的圆形梁如图8所示。

表 4 . 各种边界和载荷条件下圆形截面的命名法

图8 . 边界和载荷条件视图 (a) CC1; (b) CC2;(c)CC3
表 5描述了具有不同载荷条件和支撑条件的矩形梁截面模型以及命名法,具有载荷和边界条件的矩形梁模型视图如下图 9所示。

表 5 . 各种边界和载荷条件下实心和空心矩形截面的命名法
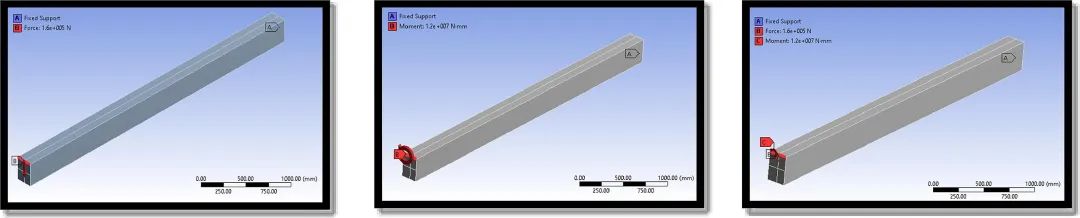
图9 . 边界和载荷条件视图 (a) RC1;(b) RC2;(c) RC3
类似地,边界条件适用于所有横截面的简支条件。下表 6描述了顶部翼缘不同载荷条件和支撑条件的建模工字梁截面以及命名法,对称工字截面的建模视图如下图 10所示。

表 6 . 对称 I 截面的命名法

图10. 边界和载荷条件视图 (a) ICT1;(b) 信息通信技术2;(c) 信息通信技术3
Results and analysis
4 Results and analysis
结果和分析
研究了同心点载荷、偏心点载荷和扭矩对所有梁截面的影响。观察了变形的类型、轴向变形的可能性和产生的应力,并在下面的图中进行了比较。
4.1 . 实心和空心圆形截面获得的结果
最大挠度、等效应力和应变的结果如下表 7所示:

表 7 . 获得圆形截面(实心和空心)的结果
实心圆梁和空心圆梁的变形以及分析后得到的应力值分别如图11和图12所示:

图11. 实心圆梁中的应力和变形视图 (a) CC1;(b) CC2;(c)CC3
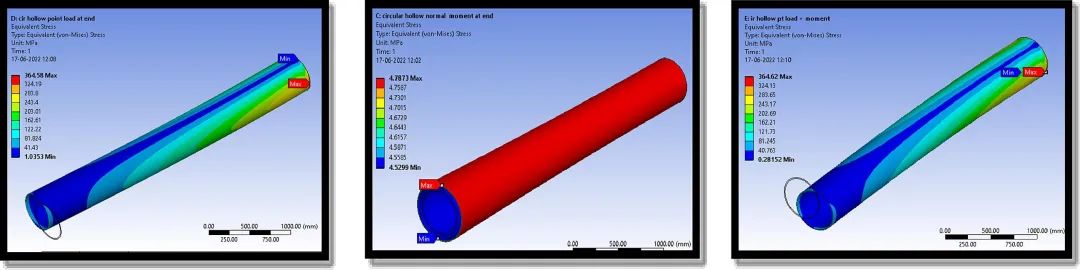
图12. 空心圆梁中的应力和变形视图 (a) HCC1;(b) HCC2;(c) HCC3
4.2 . 实心和空心矩形截面获得的结果
最大挠度、等效应力和应变的结果列于下表 8中。不同载荷和悬臂梁条件下梁的偏转形状如图13、图14、图15和图16所示。

表 8 . 实心和空心矩形截面获得的结果
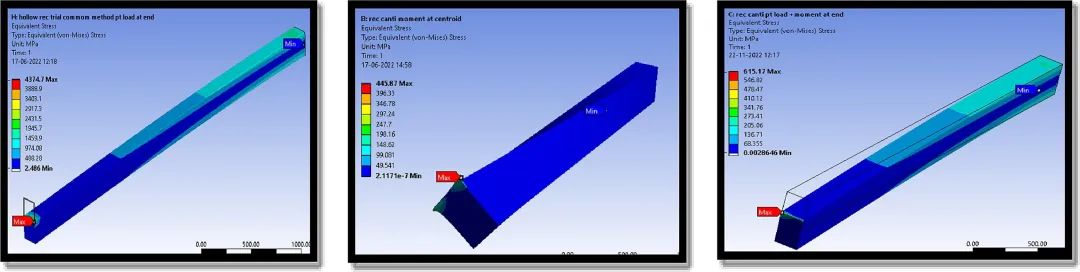
图13. 模型梁中的应力和变形视图 (a) RC1;(b) RC2;(c) RC3

图14. 模型梁中发生的应力和变形视图 (a) RHC1;(b) RHC2;(c)RHC3
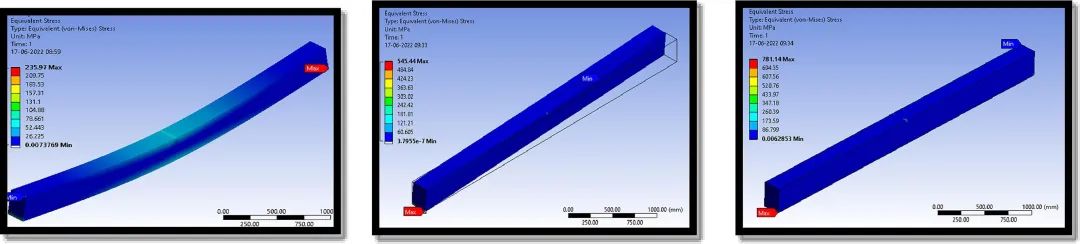
图15. 模型梁中发生的应力和变形视图 (a) RS1;(b) RS2;(一)RS3

图16. 模型梁中发生的应力和变形视图 (a) RHS1;(b) RHS2;(c) RHS3
4.3 . 对称 I 部分获得的结果
对于对称梁截面,在具有扭转力矩载荷的悬臂情况下获得了横向挠度的最大值。由于梁上的偏心载荷也导致最大应力和应变,因此出现了最大轴向挠度。长度为 4 m 的对称 I 截面获得的结果如下表 9所示,

表 9 . 获得对称 I 截面的结果
悬臂端部工字梁的挠度形状和应力如图17和图18所示。

图17. 模型梁中的应力和变形视图 (a) ICT1;(b) 信息通信技术2;(c) 信息通信技术3

图18. 模型梁中发生的应力和变形视图 (a) IST1;(b) IST2;(c) IST3
Discussion and comparison
5 Discussion and comparison
讨论与比较
根据使用 ANSYS 18.1 获得的结果,进行了以下比较并分析了载荷和支撑条件的影响。
5.1 . 悬臂梁状况
通过比较悬臂支撑条件下所有截面梁的结果,可以看出,最大轴向挠度出现在梁“CC1”中,即同心加载的圆形截面,因为圆形的抵抗横向载荷的效率较低,而抗扭转的效率较高力矩加载。对于扭转力矩载荷情况,在实心和空心圆形截面中观察到零轴向挠度。
忽略圆形截面,梁“RHC1”(即具有同心载荷的空心矩形截面)获得最大等效应力,并且在梁“RC1”(即具有同心点载荷的矩形梁)中观察到最小等效应力,如图19所示。随着载荷从同心载荷变为偏心载荷,梁中的应力增加。对于所有三种载荷情况,观察到工字梁截面的轴向挠度值高于其他截面(图 20)。
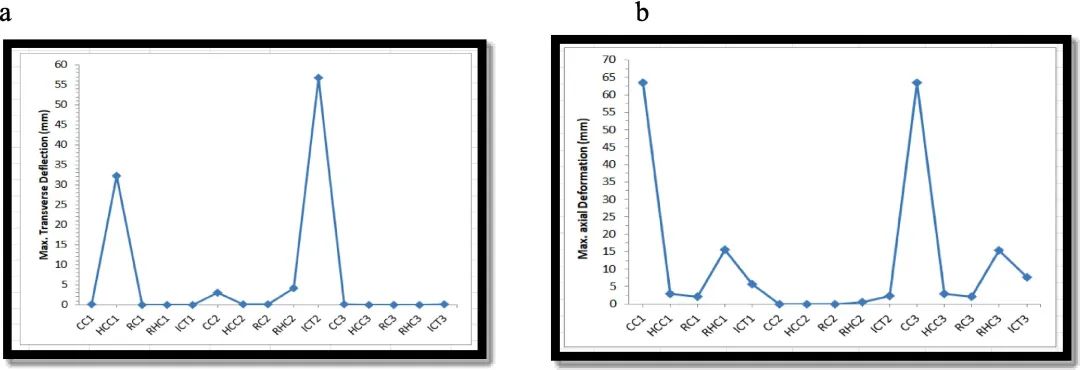
图19. 悬臂梁不同荷载情况下的最大挠度 (a) 横向;(b) 轴向
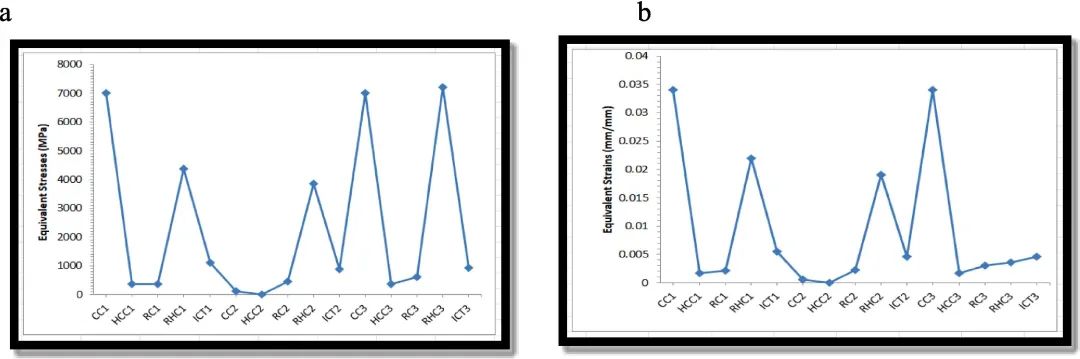
图20. 悬臂梁不同载荷工况的结果 (a) 应力;(b) 菌株
5.2 . 简支梁条件
对于梁“IST2”,即在跨度中心具有扭转力矩载荷的 I 形截面梁,观察到简支梁的最大轴向挠度。对于“RHS1”,即具有同心点载荷的矩形空心截面,观察到最小轴向挠度。结果表明,由于轴向变形值小于工字梁,空心型材能够更有效地抵抗扭转载荷。对于同心点载荷的工字形梁,观察到零轴向挠度,而对于扭转力矩和偏心点载荷,观察到最大轴向挠度,如图 21 所示,这表明开口截面在抵抗扭转和偏心效应方面的效率较低,并且对于此类负载需要次梁连接。
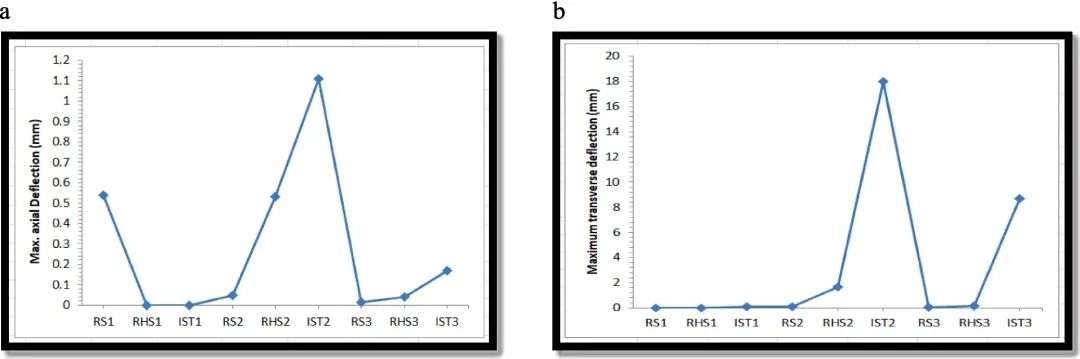
图21. 简支梁不同荷载情况下的最大挠度
(a) 横向;(b) 轴向
观察到梁“IST2”的最大横向挠度,即具有扭转力矩载荷的 I 形截面梁。对于梁情况“RS1”,即同心加载条件下的矩形梁,观察到最小横向挠度。随着载荷从同心载荷变为偏心载荷,横向挠度值增大。横向挠度的变化如图21所示。
获得“RHS3”的最大等效应变,即偏心加载条件下的空心矩形截面。对于梁“RS1”,即具有同心载荷情况的矩形梁情况,观察到最小等效应变。据观察,对于所有三种载荷工况,空心截面获得的应变值高于实心矩形或工字截面,如图 22 所示。等效应力的变化与在工况下观察到的最大等效应力的应变变化类似。“RHS3”和梁“RS1”的最小应力如图 22所示。
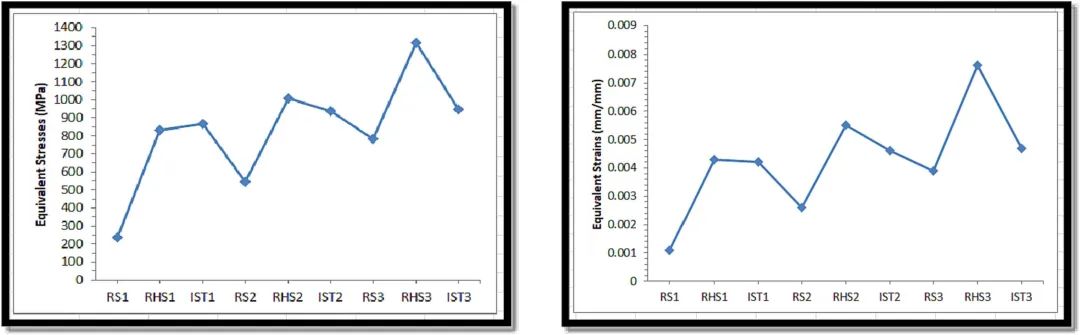
图22. 简支梁中不同载荷工况的结果 (a) 应力;(b) 菌株
Conclusions
6 Conclusions 结论
结构构件很少单独用于抵抗扭转,更常见的是沿弯曲的扭转和其他效应,例如梁上的偏心载荷会导致弯曲和扭转效应,需要对此类结构构件研究这些相互作用。根据本工作中使用 ANSYS Workbench 18.1 进行的分析研究,从分析中得出以下结论:
•目前采用ANSYS软件有限元分析方法,对不同类型荷载和支撑条件下的钢梁进行有限元分析。可以轻松估计所需位置处的应力、应变和偏转的数值分析,以及不同载荷和支撑条件下结构的变形性质和可能行为。
•梁仅表现出横向和较小的轴向偏转,但在所有截面的同心载荷条件下,横截面没有扭曲或翘曲,也没有凸缘弯曲。在简支梁和悬臂梁条件下,由于集中点载荷,不存在扭转或扭曲效应。
•对于扭转力矩和偏心载荷的情况,梁沿着梁的长度发生翘曲以及翼缘的弯曲,并且可以观察到梁的翼缘中的异常变形。
•从总体观察来看,对于对称和非对称 I 截面,在悬臂梁情况下、随后是固定梁条件和简支条件下,获得了更高的应力和应变值。
•空心型材在抵抗扭转型载荷方面表现出比实心型材和 I 型材更好的效率,而 I 型材在弯曲作用和横向载荷情况下表现出更好的效率。
工作目的已经达到,成果也已经呈现。为了找到精确的扭转角度和轴向偏转值,必须对偏心载荷和扭转载荷对这些部分的影响进行更详细的分析。应通过 ANSYS 软件包作为输出获得翘曲应力和应变值,这有利于完全理解此类分析(包括未来的工作范围)。
原始文献:
Lovely Sabat, Chinmay Kumar Kundu,
Flexural-torsional analysis of steel beam structures using ANSYS,
Materials Today: Proceedings,
2023,
,
ISSN 2214-7853,
https://doi.org/10.1016/j.matpr.2023.10.017.
(https://www.sciencedirect.com/science/article/pii/S2214785323049210)
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








