对于两轴之间的机械动力传输,正齿轮已成为人们关注的主题,其中在圆柱面上切出的齿与齿轮的轴线平行。造成齿轮组失效的主要因素是轮齿的强度。由于疲劳,齿轮齿上产生的循环应力超出了由整个齿或齿的大部分断裂引起的材料的耐受极限。在目前的工作中,齿轮的有限元分析(FEA)是在循环载荷下进行的。在循环加载的每个阶段,都会产生最大应力,并确定关键位置。正齿轮的建模是在参数化 Solid Work 软件中进行的,而 ANSYS 工作台则用于有限元分析。研究了设计参数(例如圆角半径和齿顶高)对关键位置产生的最大应力的影响。优化后的模型将轮齿最大应力降低了12.93%。这种经过优化的正齿轮现在在运行过程中具有更长的使用寿命。

本文由Google翻译,原文PDF下载链接:
https://pan.baidu.com/s/10Y49te3PdlOt470f7vvD2g
提取码:i41z
Introduction
1 Introduction介绍
对于中心距较长的两个轴之间的运动传递,通过皮带、绳索和链条进行,而对于轴之间的较短距离,则使用齿轮。齿轮基本上是一个齿轮元件,用于在不同负载条件下按照所需的运动方向在轴之间传递精确的速度比和动力传递[4],[6]。从手表等小型部件到重工业,齿轮有着广泛的应用。由于其高度可靠性和紧凑性,齿状元件是未来机器中传输动力的最有效的正向驱动装置[1]、[4]、[5]。早期齿轮是由木齿或石齿制成的,后来则由金属制成。尽管齿轮生产随着时间的推移取得了显着进步,但齿轮生产并没有常规技术,但由于弯曲和接触应力而导致的齿轮故障仍然是设计者关注的问题。
齿轮组优化设计的首要问题是应力分析、传动故障、动载荷和噪声预测。[4] . 一对正齿轮齿在作用下通常会因弯曲应力和接触应力而失效。弯曲应力产生于齿轮的齿根,而接触应力产生于齿轮的齿面[10]。这些应力在施加力的两个位置和齿根处最大。人们对该齿轮技术进行了大量的研究工作,通过考虑其材料、几何参数、制造工艺来进行改进,以最大限度地减少这种故障。有限元分析(FEA)能够在复杂的载荷条件下分析复杂形状的零件,并尽可能贴合实际情况,估算疲劳寿命,节省零件制造的时间和成本。因此,应力分析已成为消除或减少灾难性齿轮损坏以及齿轮优化设计的一个重要研究领域。
在这项工作中,通过有限元分析研究了轮齿不同位置的最大弯曲应力,并确定了轮齿失效的关键位置。将这些确定的关键位置产生的应力与之前的研究进行比较。然后,研究了圆角半径和齿顶高等设计参数对静态条件下正齿轮轮齿关键位置产生的最大应力的影响;这有助于确定最大位移、最大生成应力以及应力变化的影响,从而实现更稳健的齿轮设计。
Literature review
2 Literature review 文献综述
巴拉特·古普塔等人。研究了啮合齿轮齿之间接触应力的发展,以进行齿轮设计。他们使用 ANSYS 将重要齿轮上产生的接触应力与赫兹理论方程进行了比较。得出的结论是,可以提高齿轮齿形的硬度来防止点蚀失效,并且节点处的最大接触应力会更大,并且随着模数的增加而减小。如果在传输大量功率时最大限度地减少接触应力是首要任务,那么具有更高模数的正齿轮是更好的选择[1]。
维韦克·卡拉维尔等人。在 ANSYS 14.5 上分析了钢和灰铸铁配合齿轮之间的接触应力和变形。他们得出的结论是,铸铁比钢承受的应力更大。因此,可以根据需要将铸铁直齿轮更换为钢直齿轮,以实现高效率、长寿命和低噪音[2] 。同样,Putti Srinivasa Rao 和 Ch. Vamsi 还利用 ANSYS 15.0 工作台,利用赫兹方程和有限元分析从理论上对不同材料的不锈钢、正齿轮、结构钢、铜合金、灰口铸铁和铝合金进行接触应力分析和变形。他们得出的结论是,结构钢具有高杨氏模量和泊松比,这导致其高接触应力,而灰口铸铁具有更大的抗压强度和抗变形能力,这导致其高剪切应力[3]。
苏希尔·库马尔·蒂瓦里等人。使用有限元技术确定了渐开线正齿轮轮齿啮合时的接触应力和弯曲应力,并将结果与使用 Lewis 公式、Hurtz 方程和 AGMA/ANSI 方程获得的结果进行了比较。他们得出的结论是,赫兹理论是接触应力计算的基本理论,刘易斯公式用于计算一对齿轮的弯曲应力。[8] . Ali Raad Hassan 设计了一个程序,可以绘制啮合的成对牙齿。为了生成 10 个实例,小齿轮从第一个接触位置到最后一个接触位置每旋转 3 度就执行该程序。该应用程序生成了多个有限元模型的牙齿的可视化数据,并使用ANSYS进行应力分析[14]。将有限元分析的结果与理论计算的 结论进行比较。[9] .
S. Mahendran 等人研究了用于汽车变速箱的铸钢和复合材料正齿轮的应力分布和重量减轻。在他们的研究中。他们从研究中观察到,对于高达 1.5 KN 的塔塔超级 ACE 模型变速箱,复合材料正齿轮比铸钢正齿轮具有更小的应力、变形和重量[4]。Shubham A. Badkas 和 Nimish Ajmera [5]以及 Sushovan Ghosh等人。通过使用现有的理论模型和使用 ANSYS 的 FEM 进行分析,确定了静态和动态加载条件下弯曲应力和位移对渐开线正齿轮齿的作用[6]。他们使用 FEA 模型和分析计算发现,最大应力(约 99.45%)和位移(约 100%)出现在齿轮 齿根区域[5]。苏索万·戈什等人。通过使用 ANSYS 进行静态结构分析,在可接受的限度内的三种不同扭矩情况下,分析了正齿轮齿上的最大根部弯曲应力。他们观察到,随着扭矩条件的增加,不准确度的百分比会减小并且彼此接近[6]。T.Shoba Rani 和 T.Dada Khalandar 研究了金属正齿轮在 20 度压力角作用下齿变形时的蠕变特性。因此,随机噪声、弹性变形、制造误差和装配对准误差都会导致齿轮振动和噪声水平较高,从而导致效率损失。他们通过用尼龙齿轮代替金属铸铁齿轮来减少齿变形,证明尼龙齿轮的变形小于金属和聚碳酸酯齿轮,从而降低了噪音并延长了使用寿命[7]。
Alarazah HA 和 Abdullah MQ [12]设计、建模并分析了对称和非对称内渐开线正齿轮的弯曲应力。Jana Prithwiraj 和 Bhunia Piyal通过应力分析研究了齿轮的疲劳寿命[13]。Loc NH和Anh LT [15]模拟了齿轮的3D模型,他们将齿轮的重量优化了约43.6%至46.1%,而不影响齿轮的性能。
Problem formulation
3 Problem formulation 问题表述
3.1 . 正齿轮中的应力
在啮合的两个轮齿之间传递动力时,会受到很大的力或应力。这些作用在旋转齿轮的轮齿上的应力是根部弯曲应力和表面接触应力。正齿轮通常会由于齿上产生的弯曲或接触应力而失效,如图1所示。弯曲应力是当轮齿在特定点承受大载荷导致轮齿弯曲和疲劳时产生的正应力。最大表面接触应力影响轮齿的表面疲劳(即点蚀和磨损)。应力分析的目的是识别应力集中较多的区域,从而可能引发失效或断裂。
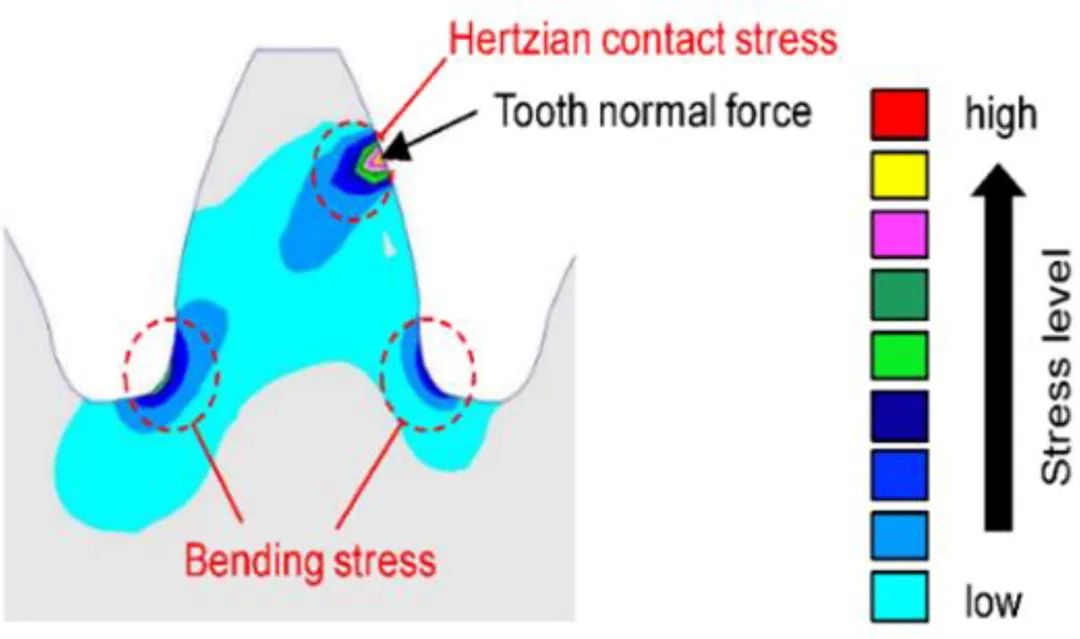
图1 . 正齿轮齿中的应力
3.2 . 正齿轮故障
疲劳是齿轮齿失效的主要原因,因为由于过度磨损、灾难性故障或整个齿或齿的大部分损坏,产生的循环应力超出了齿轮材料的耐受极限。由于动力传输过程中齿上反复产生弯曲应力,齿根圆角表面会产生疲劳裂纹,并且通常会扩展至齿根圆角表面。由于反复循环载荷的作用,轮齿会发生弯曲疲劳破坏。点蚀 是一种表面疲劳失效,其中裂纹在齿轮齿面产生。由于齿面的反复载荷而导致超过齿面的接触应力。齿轮几何形状可以通过减少负载来减少接触应力来优化[11]。
3.3 . 有限元建模
在直齿圆柱齿轮2D绘图建模阶段,使用Solid Work 2016通过拉伸、旋转、扫掠等操作将如图2 (a)所示的直齿圆柱齿轮模型转换为3D。直齿圆柱齿轮模型的尺寸取自研究论文[2]。3D 模型的准确性对于直齿轮有限元分析 (FEA) 给出最接近的结果起着重要作用。
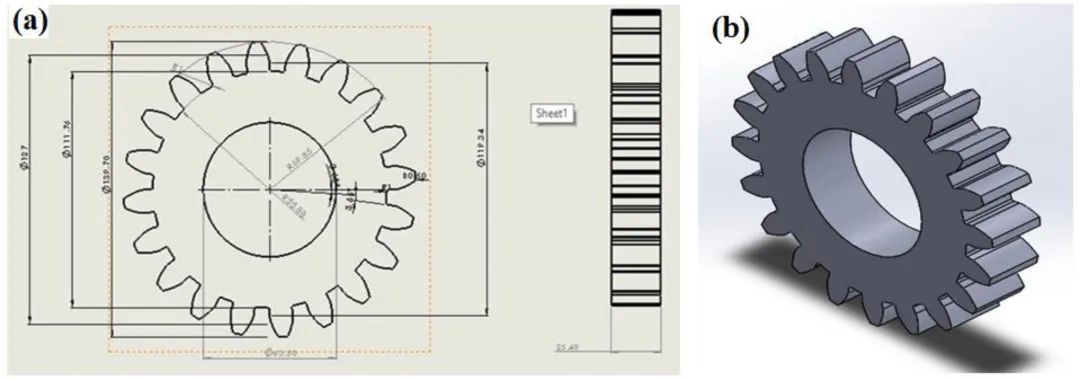
图2 . (a)正齿轮的几何形状(2D) ;(b) 正齿轮 3D 实体模型
3.4 . 有限元分析
在目前的工作中,正齿轮建模之后是网格生成、应用材料属性、定义边界条件以及应用适当的实际载荷。因此,在直齿轮模型中产生应力和位移,并对其进行研究以进行直齿轮的形状优化。
ANSYS软件是FEA解决复杂载荷结构分析和部件设计优化相关问题的重要工具。通过从 Solid Work 中以 IGES 文件格式导入直齿轮 3D 模型,在 ANSYS Workbench 上进行有限元分析。十节点四边形单元(每个节点有 3 个自由度)用于对三维模型进行网格划分,是一种高阶 3D 单元,具有二次位移行为,非常适合对不规则形状组件(例如正齿轮)进行建模。这些元素使我们能够获得更真实的结果。不同位置单元尺寸的正齿轮啮合模型如图3(a)所示。
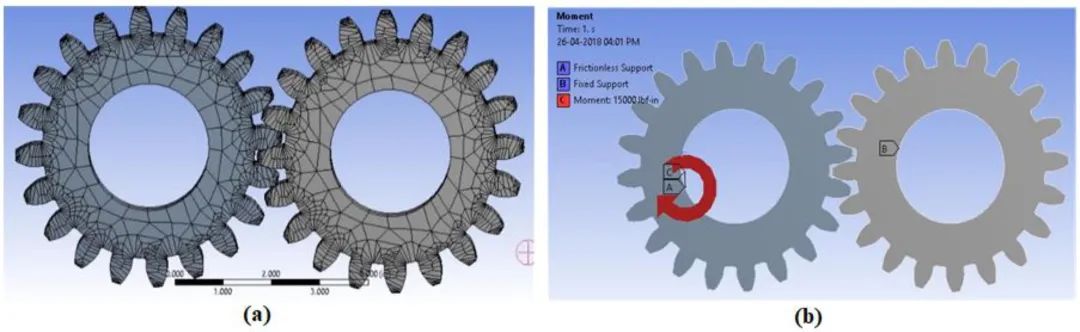
图3 . (a) 3D网格模型;(b) 正齿轮上的载荷和边界条件
有限元模型中的边界条件基于机器配置。图 3 (b) 显示了正齿轮有限元模型中定义的载荷和边界条件。为了分析直齿轮上的应力,对直齿轮模型进行了各种边界条件。在 FEM 分析中,一个正齿轮的齿根圆是固定的,而另一个(第二个)齿轮的齿根圆允许切向旋转,而径向平移受到限制。15000 lb-in 的力矩作为驱动扭矩沿顺时针方向施加在第二齿轮的根圆上。用于有限元分析的钢直齿轮的材料特性由 Vivek Karaveer等人 获得。[2]如表1所列。

表 1 . 正齿轮材料的特性
为了验证有限元分析模型,将圆角半径中的应力和其他参数与 Vivek Karaveer等人进行了比较。 [2]结果如表2所示。在目前的工作中,有限元分析是在结构钢正齿轮上进行的,其在圆角半径处产生的最大应力低估了现有的正齿轮模型 7.995%。首先,固定一个正齿轮的内轮缘,并在另一个正齿轮上施加 1694.7725 Nm 的力矩。在每个可逆循环载荷中,都会计算 Von Mises 应力,并在应力超过允许极限时定位关键位置。有限元分析是在正齿轮的不同位置进行的。结果发现,齿根处的圆角半径承受的 Von Mises 应力最高,为 3.0187e 5 (psi);因此,选为关键位置。Vivek Karaveer 等人的正齿轮圆角半径相同的齿根处产生的最大应力。 [2]发现 3.2796e 5 (psi),但与现有正齿轮模型相比存在 0.2609e 5 psi 的偏差。因此,可以认为从正齿轮模型的有限元分析中获得的结果是令人满意的,并且表明了所使用的有限元模型的准确性。

表 2 . FEA 圆角半径处生成的最大应力的比较
Shape optimization of spur gear
4 Shape optimization of spur gear
正齿轮形状优化
在优化过程阶段,必须了解部件的尺寸、使用条件、材料结构、制造工艺和其他参数,因为这会影响其成本。在这项研究服务中,负载条件用于正齿轮的有限元分析和形状优化。
目前工作的主要目标是优化正齿轮的形状以承受高强度。在这种形状优化方法中,不改变正齿轮的所有尺寸,而仅在允许限度内修改尺寸。几何特性参数用作尺寸优化中的设计变量。在这种方法中,设计变量例如齿根处的圆角半径和正齿轮的齿顶(齿高)是不同的。在直齿轮形状优化过程中,直齿轮的中心距、轮缘直径、齿顶圆半径、齿根圆半径、分度圆直径、压力角、齿面宽度等参数是固定的。分析过程中尺寸不会改变,如表3所示。


表 3 . 正齿轮形状优化的约束
图4显示了正齿轮几何优化的流程图。在优化阶段,在允许的限度内进行几何修改,以最小化正齿轮关键位置的最大应力。
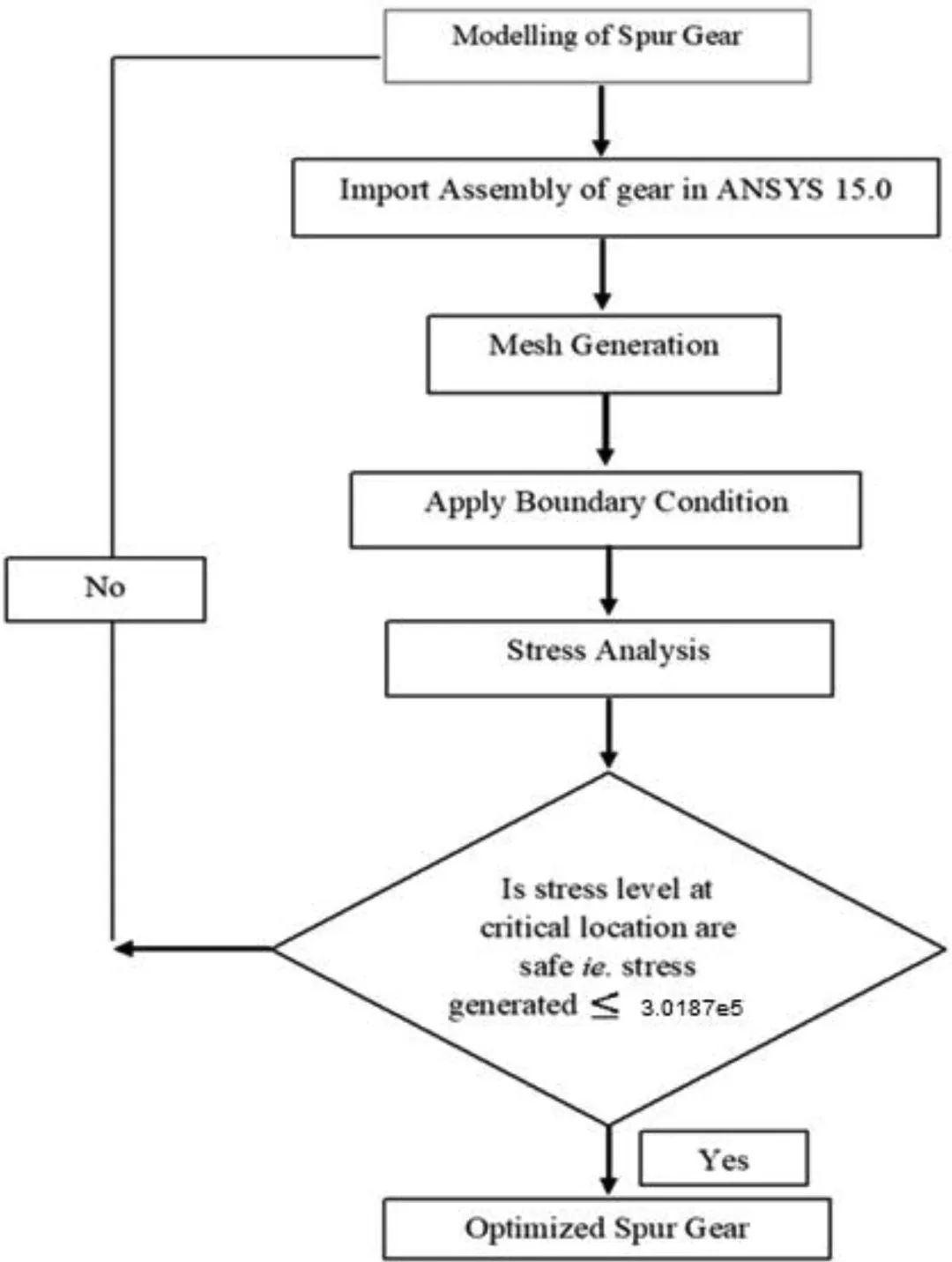
图4 . 正齿轮几何(形状)优化流程图
Result and discussion
5 Result and discussion
结果与讨论
有限元分析研究了其关键尺寸(例如齿根处的圆角半径和正齿轮的齿顶(齿高))对负载下关键位置处产生的 von-mises 最大应力的影响。假设尺寸临界值为齿根圆角半径= 1.0 mm,齿顶(齿高)= 6.3 mm,对原始正齿轮进行分析。通过考虑等质量的正齿轮,研究了设计参数对关键位置 Von Mises 应力的影响。
5.1 . 齿根圆角半径的影响
随着圆角半径的增加而产生的应力的总体减少是由于齿圆角根部处的应力集中的减少可能是优选的。由FEM分析得出;较高的圆角半径值=1.4mm可能是优选的,因为在最佳水平上是最佳的。与原始正齿轮模型相比,将圆角半径从 1.1 毫米增加到 1.5 毫米,产生的应力减少了 12.93%。表4给出了直齿轮齿根圆角半径变化时产生的应力大小。图 5显示了圆角半径为 1.4 mm 的直齿轮优化模型。

表 4 . 齿根处的圆角半径对产生的应力的影响
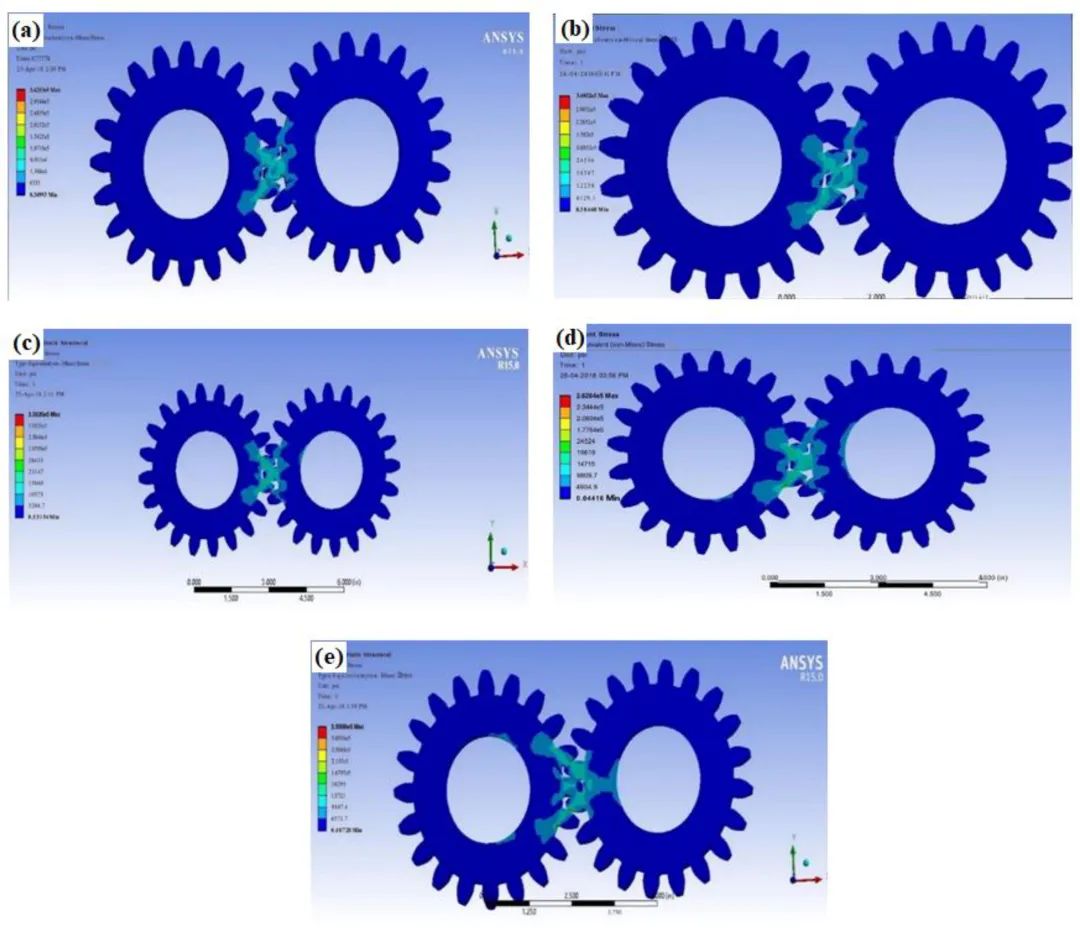
图5.圆角半径 (a) 1.1 mm 处正齿轮上产生的应力;(b)1.2毫米;(c)1.3毫米;(d)1.4毫米;(e) 1.5 毫米
5.2 . 附录的作用
另一种齿轮的步进优化不需要对几何形状进行任何复杂的改变,即改变正齿轮的齿顶(齿高)。关键位置处的应力是通过假设正齿轮所有设计参数的质量相等而获得的。通过减小齿顶(齿的高度,即从节圆到齿顶圆的径向距离),每个齿顶的关键位置处的等效(最大)应力是相同的。但齿顶距的减少避免了干涉现象;因此齿轮的寿命正在增加。
表 5显示了齿顶高对正齿轮关键位置处产生的最大应力的影响。另外,图6显示了在正齿轮齿顶高6.0mm处产生应力大小的优化模型。因此,这可以被认为是加载的安全值。因此,6.0 mm 的齿顶高可能是优化正齿轮的首选。此外,由于优化齿根圆角半径1.4 mm时产生的应力,关键位置的应力水平也降低了12.93%。

表 5 . 齿顶面对应力产生的影响

图6 . 齿顶高 6.0 mm 时正齿轮上产生的应力
5.3 . 优化后的正齿轮与原始正齿轮的比较
根据动载荷和应力分析的结果,局部几何优化分别应用于正齿轮的不同部分。表6显示了优化后的正齿轮与通过降低关键位置Von Mises应力得到的原始正齿轮的设计参数的比较。由于较高的应力集中,圆角区域的应力较高,因此第一个局部优化是将圆角半径从 1.1 mm 增加到 1.5 mm。之后,齿顶(齿高)从 6.2 毫米减少到 6.0 毫米。通过对正齿轮进行优化,可以减少产生的冯米塞斯应力。

表 6 . 优化参数与原始正齿轮模型的比较


表 7 . 优化和原始正齿轮在关键位置产生的应力比较
图7所示为优化后的直齿轮模型。这种型号的正齿轮将具有更高的耐用性。
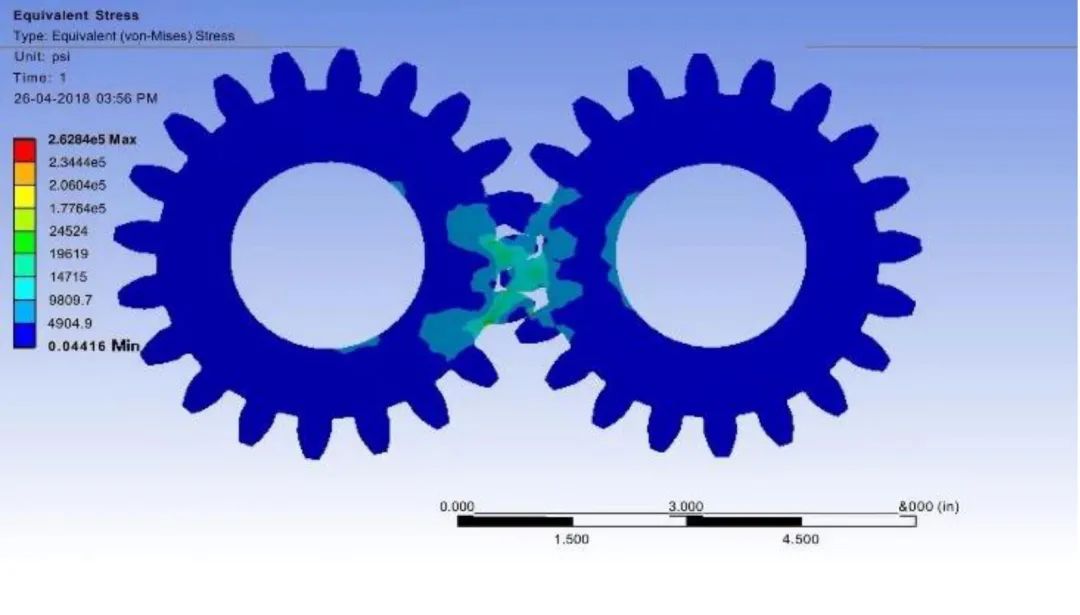
图7 . 正齿轮的优化模型
Conclusions
6 Conclusions 结论
在有限元分析中,研究复杂负载条件下正齿轮上的应力分布。分析得出以下结论:
1)正齿轮圆角半径的齿根附近的区域被发现是关键(即失效)位置,因为它承受最高的 Von Mises 应力,从而导致高应力集中系数。
2)通过对正齿轮关键尺寸的负载性能比较,得出:
a)随着圆角半径的增加,由于正齿轮圆角半径处齿根附近的应力集中减少,产生的最大应力减小。与原始正齿轮模型相比,将圆角半径从 1.1 毫米增加到 1.5 毫米,产生的应力减少了 12.93%。
b)将齿顶高从6.2mm减小到6.0mm,直齿圆柱齿轮关键部位产生的应力大小不受影响,但齿顶高的减小避免了干涉现象;因此齿轮的寿命正在增加。因此,6.0 mm 的齿顶高可能是优化正齿轮的首选。
3)因此,优化的正齿轮模型预计关键位置的 Von Mises 应力比初始设计低 12.93%。这将提供更大的强度,并提高正齿轮的耐用性。
原始文献:
Anant Prakash Agrawal, Shahazad Ali, Sachin Rathore,
Finite element stress analysis for shape optimization of spur gear using ANSYS,
Materials Today: Proceedings,
Volume 64, Part 3,
2022,
Pages 1147-1152,
ISSN 2214-7853,
https://doi.org/10.1016/j.matpr.2022.03.404.
(https://www.sciencedirect.com/science/article/pii/S2214785322017461)























 1463
1463

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








