机器学习（四）——SVM（2）

http://antkillerfarm.github.io/

拉格朗日对偶（续）

如果w不满足约束，也就是$g_i(w)>0$或$h_i(w)\ne 0$。这时由于$\mathcal{L}$函数是无约束函数，$\alpha_i$、$\beta_i$可以任意取值，因此$\sum_{i=1}^k\alpha_ig_i(w)$或$\sum_{i=1}^l\beta_ih_i(w)$并没有极值，也就是说$\theta_\mathcal{P}(w)=\infty$。

反之,如果w满足约束，则$\sum_{i=1}^k\alpha_ig_i(w)$和$\sum_{i=1}^l\beta_ih_i(w)$都为0，因此$\theta_\mathcal{P}(w)=f(w)$。

综上：

$$\theta_\mathcal{P}(w)=\begin{cases} f(w), & w满足约束 \\ \infty, & w不满足约束 \\ \end{cases}$$

我们定义：

$$p^*=\underset{w}{\operatorname{min}}\theta_\mathcal{P}(w)=\underset{w}{\operatorname{min}}\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\mathcal{L}(w,\alpha,\beta)$$

下面我们定义对偶函数：

$$\theta_\mathcal{D}(w)=\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)$$

这里的$\mathcal{D}$代表原始优化问题的对偶优化问题。仿照原始优化问题定义如下：

$$d^*=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\theta_\mathcal{D}(w)=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)$$

这里我们不加证明的给出如下公式：

$$d^*=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)\le\underset{w}{\operatorname{min}}\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\mathcal{L}(w,\alpha,\beta)=p^*$$

这样的对偶问题被称作拉格朗日对偶（Lagrange duality）。

KKT条件

拉格朗日对偶公式中使

$$p^*=d^*$$ 成立的条件，被称为KKT条件（Karush-Kuhn-Tucker conditions）：

$$\begin{align} \frac{\partial}{\partial w_i}\mathcal{L}(w^*,\alpha^*,\beta^*) & =0,i=1,\dots,n & \\ \frac{\partial}{\partial \beta_i}\mathcal{L}(w^*,\alpha^*,\beta^*) & =0,i=1,\dots,l & \\ \alpha_i^*g_i(w^*)& =0,i=1,\dots,k & \tag{1}\\ g_i(w^*)& \le 0,i=1,\dots,k & \\ \alpha_i^* & \ge 0,i=1,\dots,k & \\ \end{align}$$

其中的$w^*,\alpha^*,\beta^*$表示满足KKT条件的相应变量的取值。条件1也被称为KKT对偶互补条件（KKT dual complementarity condition）。显然这些$w^*,\alpha^*,\beta^*$既是原始问题的解，也是对偶问题的解。

严格的说，KKT条件是非线性约束优化问题存在最优解的必要条件。这个问题的充分条件比较复杂，这里不做讨论。

注：Harold William Kuhn，1925～2014，美国数学家，普林斯顿大学教授。

Albert William Tucker，1905～1995，加拿大数学家，普林斯顿大学教授。

William Karush，1917～1997，美国数学家，加州州立大学北岭分校教授。（注意，California State University和University of California是不同的学校）

支持向量

针对最优边距分类问题，我们定义：

$$g_i(w)=-y^{(i)}(w^Tx^{(i)}+b)+1\le 0$$

由KKT对偶互补条件可知，如果$\alpha_i>0$，则$g_i(w)=0$。

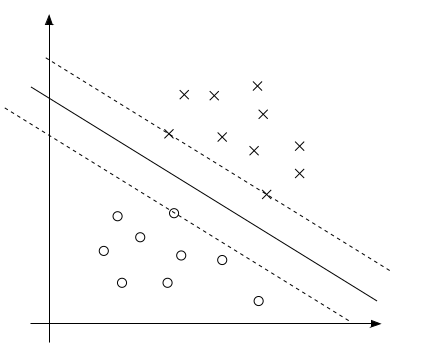
上图中的实线表示最大边距的分割超平面。由之前对于边距的几何意义的讨论可知，只有离该分界线最近的几个点（即图中的所示的两个x点和一个o点）才会取得约束条件的极值，即$g_i(w)=0$。也只有这几个点的$\alpha_i>0$，其余点的$\alpha_i=0$。这样的点被称作支持向量（support vectors）。显然支持向量的数量是远远小于样本集的数量的。

为我们的问题构建拉格朗日函数如下：

$$\mathcal{L}(w,b,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^m\alpha_i[y^{(i)}(w^Tx^{(i)}+b)-1] \tag{2}$$

为了求解

$$\theta_\mathcal{D}(\alpha)=\underset{w,b}{\operatorname{min}}\mathcal{L}(w,b,\alpha)$$

可得：

$$\nabla_w\mathcal{L}(w,b,\alpha)=w-\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}=0$$

即

$$w=\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)} \tag{3}$$

对b求导可得：

$$\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha)=\sum_{i=1}^m\alpha_iy^{(i)}=0 \tag{4}$$

把公式3代入公式2，可得：

$$\begin{align}\mathcal{L}(w,b,\alpha)&=\frac{1}{2}\|w\|^2-\sum_{i=1}^m\alpha_i[y^{(i)}(w^Tx^{(i)}+b)-1] \\&=\frac{1}{2}w^Tw-\sum_{i=1}^m\alpha_iy^{(i)}w^Tx^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}w^Tx^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}\left(\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}\right)^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}\sum_{i=1}^m\alpha_iy^{(i)}(x^{(i)})^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j(x^{(i)})^Tx^{(j)}-b\sum_{i=1}^m\alpha_iy^{(i)} \tag{5} \end{align}$$

我们定义如下内积符号$\langle x,y\rangle=x^Ty$，并将公式4代入公式5可得：

$$\mathcal{L}(w,b,\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle$$

最终我们得到如下对偶优化问题：

$$\begin{align} &\operatorname{max}_\alpha & & W(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle\\ &\operatorname{s.t.}& & \alpha_i\ge 0,i=1,\dots,m\\ & & & \sum_{i=1}^m\alpha_iy^{(i)}=0 \end{align}$$

这个对偶问题的求解，留在后面的章节。这里只讨论求解出$\alpha^*$之后的情况。

首先，根据公式3可求解$w^*$。然后

$$b^*=-\frac{\max_{i:y^{(i)}=-1}w^{*T}x^{(i)}+\min_{i:y^{(i)}=1}w^{*T}x^{(i)}}{2}$$

除此之外，我们还有：

$$w^Tx+b=\left(\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}\right)^Tx+b=\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b$$

在之前的讨论中，我们已经指出只有支持向量对应的$\alpha_i$才为非零值，因此：

$$w^Tx+b=\sum_{i\in SV}\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b$$

从上式可以看出，在空间维数比较高的情况下，SVM（support vector machines）可以有效降低计算量。

核函数

假设我们从样本点的分布中看到x和y符合3次曲线，那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维$(x,x^2,x^3)$ ，然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射（feature mapping）。

映射函数记作$\phi(x)$，在这个例子中

$$\phi(x)=\begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix}$$

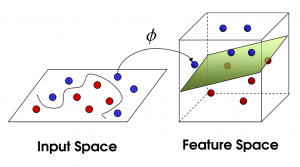
有的时候，我们希望将特征映射后的特征，而不是最初的特征，应用于SVM分类。这样做的情况，除了上面提到的拟合问题之外，还在于样例可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。如下图所示：

为此，我们给出核函数（Kernel）的形式化定义：

$$K(x,z)=\phi(x)^T\phi(z)$$

之所以是形式化定义，这主要在于我们并不利用$\phi(x)$来计算$K(x,z)$，而是给定K(x,z)，来倒推$\phi(x)$，从而建立$\phi(x)$和$K(x,z)$之间的对应关系。

例如：

$$\begin{align}K(x,z)&=(x^Tz)^2=\left(\sum_{i=1}^nx_iz_i\right)\left(\sum_{i=1}^nx_iz_i\right) \\&=\sum_{i=1}^n\sum_{j=1}^nx_ix_jz_iz_j=\sum_{i,j=1}^n(x_ix_j)(z_iz_j) \end{align}$$

根据上式可得：（这里假设$n=3$）

$$\phi(x)=\begin{bmatrix} x_1x_1 \\ x_1x_2 \\ x_1x_3 \\ x_2x_1 \\ x_2x_2 \\ x_2x_3 \\ x_3x_1 \\ x_3x_2 \\ x_3x_3 \\ \end{bmatrix}$$

可以看出$\phi(x)$的计算复杂度是$O(n^2)$，而$(x^Tz)^2$的计算复杂度是$O(n)$。

下面我们讨论其他几种常用核函数和它对应的$\phi(x)$。

$$\begin{align}K(x,z)&=(x^Tz+c)^2 \\&=\sum_{i,j=1}^n(x_ix_j)(z_iz_j)+\sum_{i=1}^n(\sqrt{2c}x_i)(\sqrt{2c}z_i)+c^2 \end{align}$$

同样的：（$n=3$）

$$\phi(x)=\begin{bmatrix} x_1x_1 \\ x_1x_2 \\ x_1x_3 \\ x_2x_1 \\ x_2x_2 \\ x_2x_3 \\ x_3x_1 \\ x_3x_2 \\ x_3x_3 \\ \sqrt{2c}x_1 \\ \sqrt{2c}x_2 \\ \sqrt{2c}x_3 \\ c \end{bmatrix}$$

更一般的，对于$K(x,z)=(x^Tz+c)^d$，其对应的$\phi(x)$是$\begin{pmatrix} n+d \\ d \\ \end{pmatrix}$维向量。

我们也可以从另外的角度观察$K(x,z)=\phi(x)^T\phi(z)$。从内积的几何意义来看，如果$\phi(x)$和$\phi(z)$夹角越小，则$K(x,z)$的值越大；反之，如果$\phi(x)$和$\phi(z)$的夹角越接近正交，则$K(x,z)$的值越小。因此，$K(x,z)$也叫做$\phi(x)$和$\phi(z)$的余弦相似度。

讨论另一个核函数：

$$K(x,z)=\exp\left(-\frac{\|x-z\|^2}{2\sigma^2}\right)$$

这个核函数被称为高斯核函数（Gaussian kernel），对应的$\phi(x)$是个无限维的向量。

注：$(a+b)^n$是个p为0.5的二项分布，由棣莫佛-拉普拉斯定理（de Moivre–Laplace theorem）可知，当$n\to\infty$时，它的极限是正态分布。

核函数的有效性

如果对于给定的核函数K，存在一个特征映射$\phi$，使得$K(x,z)=\phi(x)^T\phi(z)$，则称K为有效核函数。

我们首先假设K为有效核函数，来看看它有什么性质。假设有m个样本$\{x^{(1)},\dots,x^{(m)}\}$，我们定义$m\times m$维的矩阵k：$K_{ij}=K(x_i,x_j)$。这个矩阵被称为核矩阵（Kernel matrix）。

$$K_{ij}=K(x_i,x_j)=\phi(x^{(i)})^T\phi(x^{(j)})=\phi(x^{(j)})^T\phi(x^{(i)})=K(x_j,x_i)=K_{ji}$$

如果我们用$\phi_k(x)$表示$\phi(x)$第k个元素的话，则对于任意向量z：

$$\begin{align}z^TKz&=\sum_i\sum_jz_iK_{ij}z_j=\sum_i\sum_jz_i\phi(x^{(i)})^T\phi(x^{(j)})z_j \\&=\sum_i\sum_jz_i\sum_k\phi_k(x^{(i)})\phi_k(x^{(j)})z_j=\sum_k\sum_i\sum_jz_i\phi_k(x^{(i)})\phi_k(x^{(j)})z_j \\&=\sum_k\left(\sum_iz_i\phi_k(x^{(i)})\right)^2\ge 0 \end{align}$$

即K矩阵是半正定矩阵。事实上，K矩阵是对称半正定矩阵，不仅是K函数有效的必要条件，也是它的充分条件。相关的证明是由James Mercer给出的，被称为Mercer定理（Mercer Theorem）。

注：James Mercer，1883-1932，英国数学家，英国皇家学会会员，毕业于剑桥大学。曾服役于英国皇家海军，参加了日德兰海战。

Mercer定理给出了不用找到$\phi(x)$，而判定$K(x,z)$是否有效的方法。因此寻找$\phi(x)$的步骤就可以跳过了，直接使用$K(x,z)$替换上面公式中的$\langle x,z\rangle$即可。例如：

$$w^Tx+b=\sum_{i\in SV}\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b=\sum_{i\in SV}\alpha_iy^{(i)}K(x^{(i)},x)+b \tag{6}$$

核函数不仅仅用在SVM上，但凡在一个算法中出现了$\langle x,z\rangle$，我们都可以使用$K(x,z)$去替换，这可以很好地改善我们算法的效率。因此，核函数更多的被看作是一种技巧而非理论（kernel trick）。

规则化和不可分情况处理

我们之前讨论的情况都是建立在样例线性可分的假设上，当样例线性不可分时，我们可以尝试使用核函数来将特征映射到高维，这样很可能就可分了。然而，映射后我们也不能100%保证可分。那怎么办呢，我们需要将模型进行调整，以保证在不可分的情况下，也能够尽可能地找出分隔超平面。

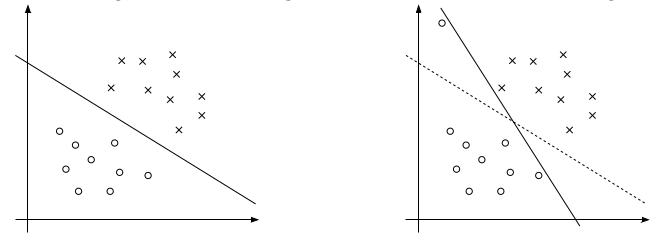
上面的右图中可以看到一个离群点（可能是噪声），它会造成超平面的移动，从而导致边距缩小，可见以前的模型对噪声非常敏感。再有甚者，如果离群点在另外一个类中，那么这时候就是线性不可分的了。