最优间隔分类器问题
本次课程大纲:
1、 最优间隔分类器
2、 原始优化问题&对偶优化问题(KKT条件)
3、 SVM对偶问题
4、 核方法(下一讲)
复习:
支撑向量机中改动的符号:
输出y∈{-1,+1}
h输出的假设值也改为{-1,+1}
g(z) = { 1 , 如果z>=0; -1, 如果z<0}
hw.b(x)=g(wTx+b),这里的b相当于原来的θ0,w相当于原来θ除去θ0剩余部分,长度为n维。将截距b单提出来,方便引出支撑向量机。
函数间隔:
一个超平面(w,b)和某个特定训练样本(x(i),y(i))对应的函数间隔定义为:
参数(w,b)定义了一个分类器,例如定义了一个线性分界线。
如果y(i)=1,为了获得较大的函数间隔,需要令wTx(i)+b >> 0;
如果y(i)=-1,为了获得较大的函数间隔,需要令wTx(i)+b << 0
如果y(i)(wTx(i)+b) > 0,意味着分类结果正确
一个超平面(w,b)和整个训练集的函数间隔定义为:
即相对于整个训练集的函数间隔定义为所有相对于样本的函数间隔的最坏情形(上述讲到,分界线距离样本越远效果越好)。
几何间隔:
几何间隔定义为:
这个定义和函数间隔很相似,不同点是对向量w进行了标准化。同样,希望几何间隔也是越大越好。
结论:如果||w||=1,函数间








 本文详细介绍了最优间隔分类器的概念,以及如何通过原始优化问题和对偶优化问题(KKT条件)解决这一问题。重点讲述了SVM的优化目标是最大化几何间隔,通过拉格朗日算子构建对偶问题,最终找到全局最优解。还提及了支撑向量和核方法在SVM中的作用。
本文详细介绍了最优间隔分类器的概念,以及如何通过原始优化问题和对偶优化问题(KKT条件)解决这一问题。重点讲述了SVM的优化目标是最大化几何间隔,通过拉格朗日算子构建对偶问题,最终找到全局最优解。还提及了支撑向量和核方法在SVM中的作用。
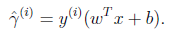
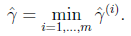
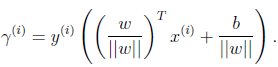
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3490
3490

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








