机器学习（十）——因子分析

http://antkillerfarm.github.io/

对$\Sigma$的限制（续）

这实际上也就是方法一中对角线元素的均值，反映到二维高斯分布图上就是椭圆变成圆。

当我们要估计出完整的$\Sigma$时，我们需要$m\ge n+1$才能保证在最大似然估计下得出的$\Sigma$是非奇异的。然而在上面的任何一种假设限定条件下，只要$m\ge 2$就可以估计出限定的$\Sigma$。

这样做的缺点也是显而易见的，我们认为特征间相互独立，这个假设太强。接下来，我们给出一种称为因子分析（factor analysis）的方法，使用更多的参数来分析特征间的关系，并且不需要计算一个完整的$\Sigma$。

利用多元高斯分布密度函数计算积分的技巧

$$I(A,b,c)=\int_x\exp\left(-\frac{1}{2}(x^TAx+x^Tb+c)\right)\mathrm{d}x$$

其中A为对称正定矩阵，b为向量。对于上面这样的积分，可以使用“完全配方法”（completion-of-squares）的数学技巧求解。

因为

$$x^TAx+x^Tb+c=(x-h)^TA(x-h)+k$$

其中$h=-\frac{A^{-1}b}{2},k=c-\frac{b^TA^{-1}b}{4}$。

所以

$$\begin{align} I(A,b,c)&=\int_x\exp\left(-\frac{1}{2}((x - h)^TA(x - h)+k)\right)\mathrm{d}x \\&=\int_x\exp\left(-\frac{1}{2}(x - h)^TA(x - h)-k/2\right)\mathrm{d}x \\&=\exp(-k/2)\cdot\int_x\exp\left(-\frac{1}{2}(x - h)^TA(x - h)\right)\mathrm{d}x \end{align}$$

令$\mu=h,\Sigma=A^{-1}$，则：

$$I(A,b,c)=\frac{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}{\exp(k/2)}\cdot\int_x\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)\mathrm{d}x$$

公式右侧的被积分函数，正好是多元高斯分布密度函数，因此该积分值为1。于是：

$$I(A,b,c)=\frac{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}{\exp(k/2)}$$

注：原始讲义里，Chuong B. Do写的《Gaussian processes》的附录A.1和本节内容类似，但推导过程有问题，疑似笔误，特更换为维基百科中的例子。（矩阵的完全配方那块的变换，我能推导出维基百科的结果，但推导不出Chuong B. Do的结果。）如有错误，望读者指出。

边缘和条件高斯分布

假设x由两个随机向量组成（可以看作是将之前的$x^{(i)}$分成了两部分）。

$$x=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

其中$x_1\in R^r,x_1\in R^s$，则x实际上是$r+s$维向量。

假设$x\sim N(\mu,\Sigma)$，其中：

$$\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix},\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}$$

因为协方差矩阵是对称矩阵，因此$\Sigma_{12}=\Sigma_{21}^T$。

$$\begin{align} Cov(x)&=\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} \\&=E\begin{bmatrix} (x-\mu)(x-\mu)^T \end{bmatrix}=E\begin{bmatrix} \begin{pmatrix} x_1-\mu_1 \\ x_2-\mu_2 \end{pmatrix} & \begin{pmatrix} x_1-\mu_1 \\ x_2-\mu_2 \end{pmatrix} \end{bmatrix} \\&=E\begin{bmatrix} (x_1-\mu_1)(x_1-\mu_1)^T & (x_1-\mu_1)(x_2-\mu_2)^T \\ (x_2-\mu_2)(x_1-\mu_1)^T & (x_2-\mu_2)(x_2-\mu_2)^T \end{bmatrix} \end{align}$$

因此，$E[x_1]=\mu_1,Cov(x_1)=E[(x_1-\mu_1)(x_1-\mu_1)^T]=\Sigma_{11}$。可见，多元高斯分布的边缘分布仍然是多元高斯分布。

下面讨论一下条件高斯分布。

$$\begin{align} p(x_1\vert x_2)&=\frac{p(x_1,x_2)}{p(x_2)}=\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)}{\int_{x_1}p(x_1,x_2;\mu,\Sigma)\mathrm{d}x_1} \\&=\frac{1}{Z_1}\exp\left\{-\frac{1}{2}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)^T\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)\right\} \end{align}$$

其中的$Z_1$是和$x_1$无关的部分，可看作常数，下面的$Z_i$也是同理。

$$\Sigma^{-1}=V=\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}$$

因为：

$$\begin{align} &\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)^T\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right) \\&=(x_1-\mu_1)^TV_{11}(x_1-\mu_1)+(x_1-\mu_1)^TV_{12}(x_2-\mu_2) \\&\qquad+(x_2-\mu_2)^TV_{21}(x_1-\mu_1)+(x_2-\mu_2)^TV_{22}(x_2-\mu_2) \end{align}$$

保留上式中与$x_1$有关的部分，可得：

$$p(x_1\vert x_2)=\frac{1}{Z_2}\exp\left(-\frac{1}{2}\left(x_1^TV_{11}x_1-2x_1^TV_{11}\mu_1+2x_1^TV_{12}(x_2-\mu_2)\right)\right)$$

使用上一节中的完全配方技巧，可得：

$$p(x_1\vert x_2)=\frac{1}{Z_3}\exp\left(-\frac{1}{2}(x_1-\mu_{1\vert 2})^TV_{11}(x_1-\mu_{1\vert 2})\right)$$

其中：

$$\mu_{1\vert 2}=\mu_1-V_{11}^{-1}V_{12}(x_2-\mu_2)\tag{1}$$

即：

$$x_1\vert x_2\sim N(\mu_1-V_{11}^{-1}V_{12}(x_2-\mu_2),V_{11}^{-1})$$

另，根据分块矩阵的求逆法则，可得：

$$\Sigma^{-1}=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}^{-1}=\begin{bmatrix} (\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1} & -(\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1}\Sigma_{12}\Sigma_{22}^{-1} \\ -\Sigma_{22}^{-1}\Sigma_{21}(\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1} & (\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12})^{-1} \end{bmatrix}$$

因此：

$$\Sigma_{1\vert 2}=V_{11}^{-1}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}\tag{2}$$

因子分析的例子

下面通过一个简单例子，来引出因子分析背后的思想。

假设我们有m=5个2维的样本点$x^{i}$，如下：

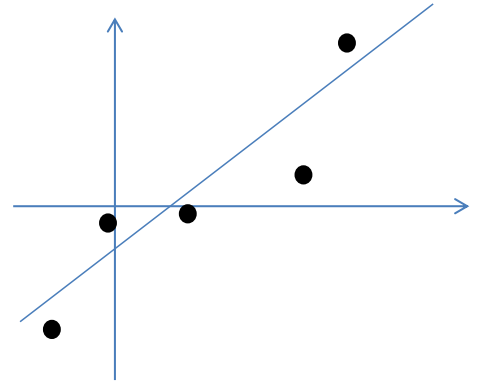
按照因子分析模型，样本点的生成过程如下：

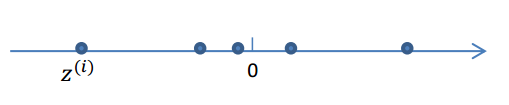
1.我们首先认为在1维空间（这里k=1），存在着按正态分布生成的m个点$z^{(i)}$，即：

$$z^{(i)}\sim N(0,I)$$

这里的I是单位矩阵。

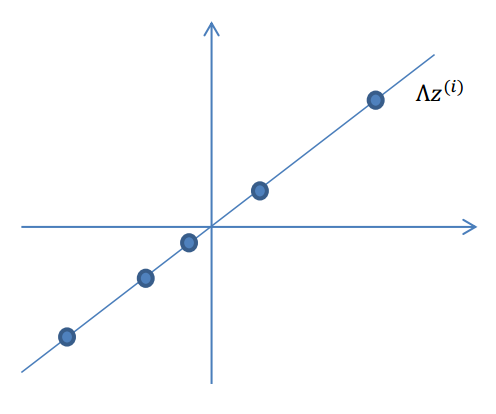
2.使用变换矩阵$\Lambda\in R^{n\times k}$，将$z^{(i)}$映射到n维空间中，即$\Lambda z^{(i)}$。

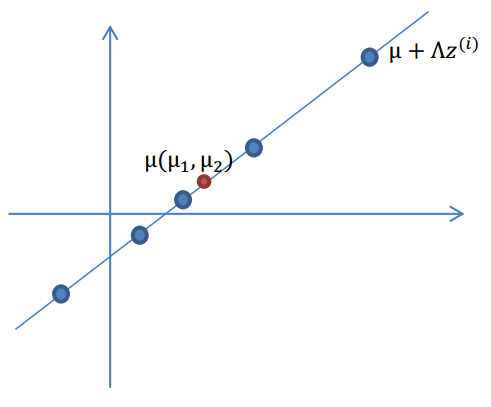
3.使用n维向量$\mu$，将$\Lambda z^{(i)}$移动到样本的中心点$\mu$，即$\mu+\Lambda z^{(i)}$

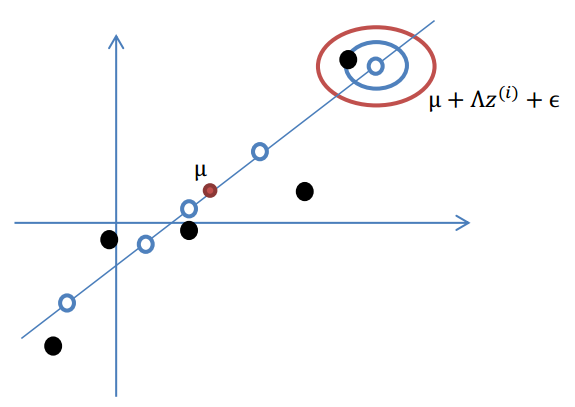
4.样本点不可能这么规则，在模型上会有一定偏差，因此我们需要将上步生成的点做一些扰动（误差）。这里添加一个n维的扰动向量$\epsilon \sim N(0,\Psi)$。

综上可得:

$$x^{(i)}=\mu+\Lambda z^{(i)}+\epsilon$$

$$x \vert z\sim N(\mu+\Lambda z,\Psi)$$

由以上的直观分析，我们知道了因子分析其实就是认为：高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的，因此高维数据可以使用低维来表示。

线性回归的概率模型

在进一步讨论因子分析模型之前，我们首先讨论一下，和它类似的线性回归的概率模型。

从概率的角度看，线性回归中的$y^{(i)}$可以看作是预测函数$h_\theta(x)$加上扰动后的结果。即：

$$y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)},\epsilon^{(i)}\sim N(0,\sigma^2)$$

$$p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right)$$

$$p(y^{(i)}\vert x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right)$$

$$\begin{align} \ell(\theta)&=\log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right)=\sum_{i=1}^m\log\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right) \\&=m\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-\theta^Tx^{(i)}\right)^2 \end{align}$$

从上式可以看出采用极大似然估计和采用代价函数$J(\theta)$的效果是一样的。其中：

$$J(\theta)=\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-\theta^Tx^{(i)}\right)^2$$

因子分析模型

假设z和x的联合分布为：

$$\begin{bmatrix} z \\ x \end{bmatrix}\sim N(\mu_{zx},\Sigma)$$

我们的任务就是求出$\mu_{zx}$和$\Sigma$。

因为：

$$E[x]=E[\mu+\Lambda z+\epsilon]=\mu+\Lambda E[z]+E[\epsilon]=\mu$$

所以：

$$\mu_{zx}=\begin{bmatrix} \vec{0} \\ \mu \end{bmatrix}$$

因为：

$$\Sigma=\begin{bmatrix} \Sigma_{zz} & \Sigma_{zx} \\ \Sigma_{xz} & \Sigma_{xx} \end{bmatrix}$$

所以我们只要分别计算这四个值即可。

因为$z\sim N(0,I)$，所以$\Sigma_{zz}=I$。

$$\begin{align} \Sigma_{zx}&=E[(z-E[z])(x-E[x])^T]=E[(z-0)(\mu+\Lambda z+\epsilon-\mu)^T]=E[z(\Lambda z+\epsilon)^T] \\&=E[z(\Lambda z)^T+z\epsilon^T]=E[zz^T\Lambda^T+z\epsilon^T]=E[zz^T]\Lambda^T+E[z\epsilon^T] \end{align}$$

因为z和$\epsilon$是相互独立的随机变量，因此$E[z\epsilon^T]=E[z]E[\epsilon^T]=0$。

又因为$E[zz^T]=Cov(z)=I$，所以$\Sigma_{zx}=\Lambda^T$。

$$\begin{align} \Sigma_{xx}&=E[(x-E[x])(x-E[x])^T]=E[(\mu+\Lambda z+\epsilon-\mu)(\mu+\Lambda z+\epsilon-\mu)^T] \\&=E[(\Lambda z+\epsilon)(\Lambda z^T+\epsilon^T)]=E[\Lambda z(\Lambda z)^T+\epsilon(\Lambda z)^T+\Lambda z\epsilon^T+\epsilon\epsilon^T] \\&=E[\Lambda zz^T\Lambda^T+\epsilon z^T\Lambda^T+\Lambda z\epsilon^T+\epsilon\epsilon^T] \\&=\Lambda E[zz^T]\Lambda^T+E[\epsilon z^T]\Lambda^T+\Lambda E[z\epsilon^T]+E[\epsilon\epsilon^T] \\&=\Lambda I\Lambda^T+0+0+\Psi=\Lambda \Lambda^T+\Psi \end{align}$$

把这些结果合在一起，可得：

$$\begin{bmatrix} z \\ x \end{bmatrix}\sim N\left(\begin{bmatrix} \vec{0} \\ \mu \end{bmatrix},\begin{bmatrix} I & \Lambda^T \\ \Lambda & \Lambda \Lambda^T+\Psi \end{bmatrix}\right)\tag{3}$$

从这个结论可以看出：$x\sim N(\mu,\Lambda \Lambda^T+\Psi)$

因此它的对数似然函数为：

$$\ell(\mu,\Lambda,\Psi)=\log\prod_{i=1}^m\frac{1}{(2\pi)^{n/2}\lvert\Lambda \Lambda^T+\Psi\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu)^T(\Lambda \Lambda^T+\Psi)^{-1}(x^{(i)}-\mu)\right)$$

但这个函数是很难最大化的，需要使用EM算法解决之。

因子分析的EM估计

E-step比较简单。由公式1、2、3，可得：

$$\mu_{z^{(i)}\vert x^{(i)}}=\Lambda^T(\Lambda \Lambda^T+\Psi)^{-1}(x^{(i)}-\mu)$$

$$\Sigma_{z^{(i)}\vert x^{(i)}}=I-\Lambda^T(\Lambda \Lambda^T+\Psi)^{-1}\Lambda$$

因此：

$$Q_i(z^{(i)})=\frac{1}{(2\pi)^{n/2}\lvert\Sigma_{z^{(i)}\vert x^{(i)}}\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_{z^{(i)}\vert x^{(i)}})^T\Sigma_{z^{(i)}\vert x^{(i)}}^{-1}(x^{(i)}-\mu_{z^{(i)}\vert x^{(i)}})\right)$$

M-step的最大化的目标是：

$$\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\mu,\Lambda,\Psi)}{Q_i(z^{(i)})}\mathrm{d}z^{(i)}$$

下面我们重点求$\Lambda$的估计公式。

首先将上式简化为:

$$\begin{align} &\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)}\vert z^{(i)};\mu,\Lambda,\Psi)p(z^{(i)})}{Q_i(z^{(i)})}\mathrm{d}z^{(i)} \\&=\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\left[\log p(x^{(i)}\vert z^{(i)};\mu,\Lambda,\Psi)+\log p(z^{(i)})-\log Q_i(z^{(i)})\right]\mathrm{d}z^{(i)} \\&=\sum_{i=1}^m E_{z^{(i)}\sim Q_i}\left[\log p(x^{(i)}\vert z^{(i)};\mu,\Lambda,\Psi)+\log p(z^{(i)})-\log Q_i(z^{(i)})\right] \end{align}$$