主成分分析

最新推荐文章于 2024-07-12 19:30:19 发布

花咲溶溶月

最新推荐文章于 2024-07-12 19:30:19 发布

阅读量114

点赞数

分类专栏： Python 点云文章标签： python 线性代数

本文链接：https://blog.csdn.net/apple_51522252/article/details/132386215

版权

Python 同时被 2 个专栏收录

6 篇文章 0 订阅

订阅专栏

点云

3 篇文章 0 订阅

订阅专栏

主成分分析(Principle Component Analysis)，是一种数据降维算法，其原理就是通过在原始的坐标系中找一组互相垂直的基底形成新的坐标系，将原始数据从 $n$ 个维度降低到 $k$ 个维度。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第 $1, 2$ 个轴正交的平面中方差最大的。依次类推，可以得到 $k$ 个这样的坐标轴。方差最大是为了保证能够尽可能多的保留原始数据信息。

1 前置知识

1.1 谱定理

若 $A$ 为对称矩阵，同时 $\lambda_i$ 为该矩阵的特征值，那么有：

$U\Lambda U^T = \Sigma^n_{i = 1}\lambda_iu_iu_i^T.\Lambda=diag(\lambda_1,...,\lambda_n)$

其中， $U$ 为正交矩阵，即 $UU^T = U^TU = I_n$

1.2 瑞利商定理

对于给定的对称矩阵 $\in S^n$ ，有

$\lambda_{min}(A) \leq \frac{x^TAx}{x^Tx} \leq \lambda_{max}(A), \forall x\neq0$

1.3 奇异值分解（SVD）

奇异值分解不需要矩阵 $A$ 为方阵，假设这是一个 $m * n$ 的矩阵，那么就会有：

$U\Sigma V^T = \sum_{i = 1}\sigma_iu_iv_i^T$

其中 $U$ 是一个 $m * m$ 的矩阵， $\Sigma$ 是一个 $m * n$ 的矩阵，主对角线上以外的元素全为 $0$ ，主对角线上的每个元素都称为奇异值， $V$ 是一个 $n * n$ 的矩阵。 $U$ 和 $V$ 都是酉矩阵，也就是满足 $U^TU=I,V^TV=I$ 。

2 PCA

2.1 输入输出

$PC A$ 的输入为多个向量，每个向量代表一个点。即输入为 $x_i \in R^n, i = 1, 2, ..., m$

输出则为 $k$ 个主要方向向量，也就是 $z_1, z_2, ..., z_k \in R^n, k\leq n$

2.2 计算原理

首先将数据标准化，也就是将坐标原点移动到数据中心处。计算方法为 $\tilde X = [\tilde x_1, ..., \tilde x_m], \tilde x_i = x_i - \bar x. i = 1, ..., m$
之后，将每个点投影到方向 $z$ 上，其中 $\in R^n, ||z||_2 = 1$ 。有 $\alpha_i = \tilde x^T_iz, i=1, ..., m$
我们知道，能够尽可能保留更多原始信息的方向应该满足在这个方向上的投影方差最大。因此我们对投影方向上的方差进行计算。计算公式为： $\frac{1}{m}\Sigma^{m}_{i = 1}\alpha_i^2 = \frac{1}{m}\Sigma^{m}_{i = 1}z^T\tilde x_i \tilde x_i^Tz = \frac{1}{m}z^T\tilde X \tilde X^Tz$
将其最大化，实际上就是一个优化问题，也就是寻求 $max_{z\in R^n}z^T(\tilde X \tilde X^T)z,s.t.:||z||_2 = 1$
对 $\tilde X$ 下手，对其应用 $S V D$ ，就可以得到 $\tilde X = U_r\Sigma V_r^T$
那么 $\tilde X \tilde X^T = U_r\Sigma V_r^T(U_r\Sigma V_r^T)^T = U_r\Sigma V_r^TV\Sigma^T U_r^T = U_r\Sigma ^ 2U_r^T$
接下来就是要求一下第二个主要坐标轴。首先需要吧主成分 $1$ 中的内容删除掉。也就是 $\tilde x_i^{(1)} = \tilde x_i - u_1(u_1^T\tilde x_i),i=1,...,m$
那么就有 $\tilde X^{(1)} = [\tilde x_1^{(1)},...,\tilde x_m^{(1)}] = (I_n - u_1u_1^T)\tilde X$
应用一下 $S V D$ ，就可以有 $\tilde X^{(1)} = \sum_{i = 1}^r\sigma_iu_iv_i^T - (u_1u_1^T)\sum_{i = 1}^r\sigma_iu_iv_i^T$
后面部分可以转化为 $\sum_{i = 1}^r\sigma_iu_1u_1^Tu_iv_i^T$ ，而 $u_1^Tu_i = 1$ ，所以有最终 $\tilde X^{(1)} = \sum_{i = 1}^r\sigma_iu_iv_i^T - \sigma_1u_1v_1^T = \sum_{i = 2}^r\sigma_iu_iv_i^T$
之后要求 $z_2$ ，即优化问题 $max_{z\in R^n}z^T(\tilde X^{(1)}\tilde X^{(1)T})z,s.t.:||z||_2=1\ \ \tilde X^{(1)} = \sum_{i = 2}^r\sigma_iu_iv_i^T$
最终结果即为 $z_2 = u_2$ ， $u_2$ 就是 $U_r$ 矩阵的第二行
之后的结果也类似……

综上所述，求取坐标轴的方法分为三步：

数据标准化。 也就是 $\tilde X = [\tilde x_1, ..., \tilde x_m], \tilde x_i = x_i - \bar x. i = 1, ..., m$ ；
计算 $\tilde X \tilde X^T$ 的 $S V D 。$
最终结果就是 $S V D$ 求得的 $U_r$ 。

2.3 代码实现

def PCA(data):
    mean = np.mean(data, axis=0)
    X_mean = data - mean
    # 协方差矩阵
    # 要转置是因为numpy中的协方差矩阵是以行为一个向量的
    H = np.cov(X_mean.T)
    # 之后计算其SVD，求出特征值和特征向量
    eigenvalues, eigenvectors = np.linalg.eig(H)
    # 然后对特征值进行排序，根据特征值排序特征向量
    sorted = eigenvalues.argsort()[::-1] # 从大到小的索引值
    eigenvalues = eigenvalues[sorted]
    eigenvectors = eigenvectors[:, sorted]
    return eigenvalues, eigenvectors

3 Kernel PCA

第二节我们所介绍的内容被称为线性 $PC A$ ，那么有些情况下会导致无法使用线性变换的方法得到合适的坐标轴来完成目的。比如说下图数据。

这样的数据，我们就很难通过线性变换的方法去找到合适的坐标系去将红色的点和绿色的点分开。那应该怎么办呢？简单来说，就是应该先升维处理，然后再进行和线性 $PC A$ 一致的操作。 上面的图当例子来说，升维之后，说不定就能分开了呢？你别说，还真可以，升维后的结果可以如下图：

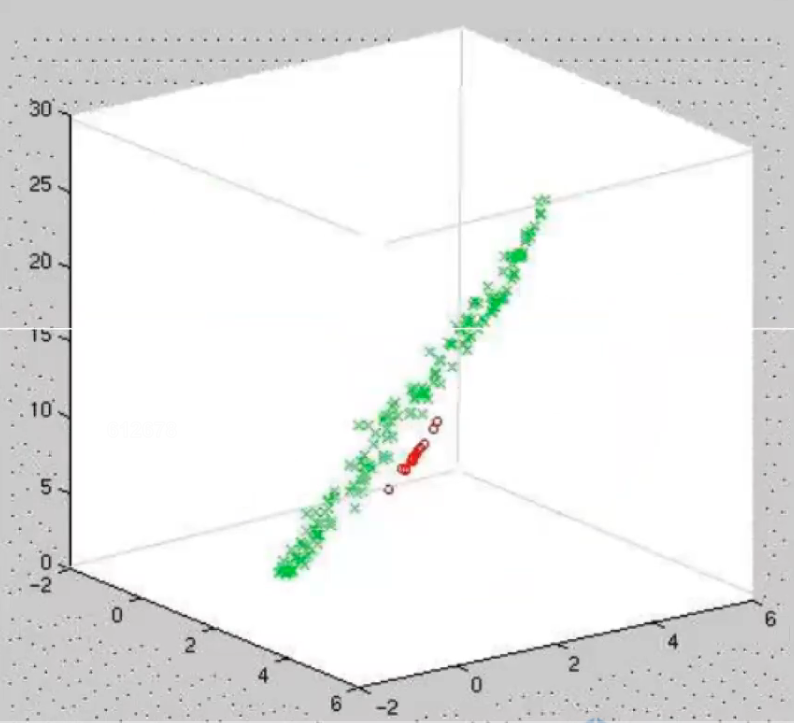
这个时候就可以通过线性变换找到坐标系来处理了！

3.1 基本思路

首先，我们要将数据进行升维，那肯定是要有一个升维函数的对吧！比如说上面那个例子，里面的每个数据点包含的信息为二维信息，即 $x_i = [x_{i1}, x_{i2}]\in R^2$ ，那么我们的升维函数就是 $\phi(x_i) = [x_{i1}, x_{i2}, x_{i1}^2 + x_{i2}^2]\in R^3$

还是跟线性 $PC A$ 一样分三步！

首先将升维之后的数据标准化，也就是令 $\frac{1}{N}\sum_{i = 1}^N\phi(x_i)=0$
之后还是要计算协方差矩阵 $\tilde H = \frac{1}{N}\sum_{i = 1}^N\phi(x_i)\phi^T(x_i)$ 。为什么这里矩阵和转置的位置调换过来了呢？这是因为在进行核 $PC A$ 操作的时候，每个点的信息已经都存储为列向量了，而再线性 $PC A$ 中是以行向量的方式存储的，有所差别，因此在这里两者换了一下方向。
最终就是要求协方差矩阵的特征值，也就是 $\tilde H \tilde z = \tilde \lambda \tilde z$

但是并不是只是这样就可以了，还存在有两个问题。升维函数 $\phi$ 应该如何定义？以及能不能不要在这么高维度的情况下计算？要不然计算量也太大了。答案是：当然可以！

我们实际上要求的就是特征值 $\tilde z$ 对吧，包括在线性 $PC A$ 中我们也是通过 $S V D$ 来求特征值矩阵的。那么我们大胆猜测，对于升维后的 $\phi(x_j)$ ，每一个都乘以一个系数，最后一定能凑出来 $\tilde z$ 的，也就是说

$\tilde z = \sum_{j = 1}^N\alpha_j\phi(x_j)$

这个是可以证明的，但是在这里就不提及了。这个公式所代表的意义就是说，我们要求 $\tilde z$ ，实际上只要求出 $\alpha_j$ 就可以了。

好好好，接下来我们把之前我们搞的这个 $\tilde H = \frac{1}{N}\sum_{i = 1}^N\phi(x_i)\phi^T(x_i)$ 和 $\tilde z = \sum_{j = 1}^N\alpha_j\phi(x_j)$ 导入到我们的特征值方程 $\tilde H \tilde z = \tilde \lambda \tilde z$ 中，就得到了：

$\frac{1}{N}\sum_{i = 1}^N\phi(x_i)\phi^T(x_i)(\sum_{j = 1}^N\alpha_j\phi(x_j)) = \tilde \lambda \sum_{j = 1}^N\alpha_j\phi(x_j)$

简单应用一下结合律：

$\frac{1}{N}\sum_{i = 1}^N\phi(x_i)(\sum_{j = 1}^N\alpha_j\phi^T(x_i)\phi(x_j)) = \tilde \lambda \sum_{j = 1}^N\alpha_j\phi(x_j)$

接下来是重点！我们定义核函数 $k(x_i, x_j) = \phi^T(x_i)\phi(x_j)$ ，那么上面的公式就可以转化为：

$\frac{1}{N}\sum_{i = 1}^N\phi(x_i)(\sum_{j = 1}^N\alpha_jk(x_i, x_j)) = \tilde \lambda \sum_{j = 1}^N\alpha_j\phi(x_j)$

还能输出！两边都左乘 $\phi(x_k), k = 1, ..., N$ ，实际上就是乘进了 $i$ 的循环对吧，那么就变成了（注意 $\frac{1}{N}$ 乘过去了）：

$\sum_{i = 1}^N \sum_{j = 1}^N \alpha_jk(x_k, x_i)k(x_i, x_j) = N \tilde \lambda \sum_{j = 1} ^ N \alpha_jk(x_k, x_j), k = 1, ..., N$

然后我们定义一个格拉姆矩阵（多个向量之间任意两两相乘） $\in R^{N*N}, K(i, j) = k(x_i, x_j)$ ，他还是对称矩阵，这个还是很好想的，毕竟 $k(x_i, x_j) = k(x_j, x_i)$

那么上面的公式就可以改写为

$K^2\alpha = N\tilde \lambda K \alpha$

两边消掉一个 $K$ ，变成 $K\alpha = N\tilde \lambda \alpha$

那反正 $N$ 和 $\tilde \lambda$ 都是数字， $N$ 还是个常数，那不如直接把他俩整合为 $\lambda$ ，也就会变为： $K\alpha = \lambda \alpha$

好，这个时候我们想一想， $\tilde z = \sum_{j = 1}^N \alpha_j\phi(x_j)$ ，由于他应该是方向向量，也就是 $||\tilde z||_2 = 1$ ，所以有 $\tilde z^T\tilde z$

把 $\tilde z$ 的表达式代入，就可以得到 $\sum_{i = 1}^N \sum_{j = 1}^N \alpha_{ri} \alpha_{rj}\phi^T(x_i)\phi(x_j)$

应用一下核函数，他就变成了 $\alpha_r^TK\alpha_r$

那么我们刚刚已经看到了有公式 $K\alpha = \lambda \alpha$ ，也就是说上面的式子就可以转化为 $\alpha_r^T\lambda_r\alpha_r = 1$

也就是说， $\alpha_r$ 的长度应该为 $1/\lambda_r$

之后我们把升维之后的向量投影到 $\tilde z_r$ 上，也就能够得到 $\phi^T(x)\tilde z_r = \sum_{j = 1}^N \alpha_{rj}\phi^T(x)\phi(x_j) = \sum_{j = 1}^N\alpha_{rj}k(x, x_j)$

还有一件事，就是要把 $\phi(x_i)$ 标准化，也就是让平均值为 $0$ ，也就是 $\tilde \phi(x_i) = \phi(x_i) - \frac{1}{N}\sum_{j=1}^N\phi(x_j)$

随之而来的还有对核函数进行标准化，也就是 $\tilde k(x_i, x_j) = \tilde \phi^T(x_i)\tilde \phi(x_j)$

$(\phi(x_i) - \frac{1}{N}\sum_{k = 1}^N\phi(x_k))^T(\phi(x_j) - \frac{1}{N}\sum_{i = 1}^N\phi(x_l))$

$k(x_i, x_j) - \frac{1}{N}\sum_{k = 1}^Nk(x_i, x_k) - \frac{1}{N}\sum_{k = 1}^Nk(x_j, x_k) + \frac{1}{N^2}\sum_{k = 1}^N\sum_{l = 1}^Nk(x_k, x_l)$

将这个极其复杂的公式再用 $K$ 来转化，就可以转化为 $\tilde K = K - 2 * I_{\frac{1}{N}}K + I_{\frac{1}{N}}K I_{\frac{1}{N}}$ ，其中 $I_{\frac{1}{N}} = \frac{1}{N}$

3.2 常用的核函数

常用的核函数主要包括：

线性函数 $k(x_i, x_j) = x_i^Tx_j$
多项式函数 $k(x_i, x_j) = (1 + x_i^Tx_j)^p$
高斯函数 $k(x_i, x_j) = e^{-\beta||x_i - x_j||_2}$
拉普拉斯函数 $k(x_i, x_j) = e^{-\beta||x_i - x_j||_1}$

3.3 总结思路

选择而一个核函数 $k(x_i, x_j)$ ，并计算与之对应的格拉姆矩阵 $K(i, j) = k(x_i, x_j)$
将 $K$ 标准化，也就是令 $\tilde K = K - 2 * I_{\frac{1}{N}}K + I_{\frac{1}{N}}K I_{\frac{1}{N}}$
求解 $\tilde K$ 的特征向量/特征值，即 $\tilde K \alpha_r = \lambda_r\alpha_r$
然后将 $\alpha_r$ 标准化，也就是令 $\alpha_r^T\alpha_r = \frac{1}{\lambda_r}$
对于任意数据点 $\in R^n$ ，计算其在第 $r$ 个主成分 $y_r \in R$ 上的投影，也就是 $y_r = \phi^T(x)\tilde z_r = \sum_{j = 1}^N\alpha_{rj}k(x, x_j)$