聚类方法小全（一）

1 K-means

K-means是最简单且十分好用的聚类方法，其所实现的功能就是将$N$个点分为$K$类。它的基本步骤可以分为四步：

• 随机选取$K$个中心点
• 将所有的$N$个点都分配到这$K$个中心点中去
• 将每一个组的中心点重新作为$K$个中心点
• 重复步骤$2$和步骤$3$

1.1 相关定义

要介绍这样一个算法，我们首先要明白一下定义：

• 我们的数据集为 { x 1 , x 2 , . . . , x N } , x n ∈ R D \{x_1, x_2, ..., x_N\}, x_n \in R^D {x1​,x2​,...,xN​},xn​∈RD
• 聚类中心（就是我们要找的$K$个中心点）${\mu }_k,k=1,2,...,K$
• 布尔类型的变量 r n k ∈ { 0 , 1 } r_{nk}\in\{0, 1\} rnk​∈{0,1}， 表示对于第$n$个点，如果它输入第$k$类，那么$r_{nk}=1$， 否则$r_{nk}=0$
• 做K-means的最终目标就是最小化$J={\sum }_{n=1}^N{\sum }_{n=1}^K{r}_{nk}||x_n-{\mu }_k|{|}^2$

1.2 迭代方法

要实现这样的最终目标，我们需要简单的借助$EM$的思想，具体的$EM$介绍我会放在后面。简单来说就是需要迭代$r_{nk}$和${\mu }_k$的值。

• **E(expectation)步骤：**固定${\mu }_k$，在最小化$J$的情况下求解$r_{nk}$。这一步很简单，只需要对每一个点进行操作，找出每一个点最近的${\mu }_k$，然后使得这个点的$r_{nk}=1$。
• **M(maximization)步骤：**固定$r_{nk}$，在最小化$J$的情况下求解${\mu }_k$。这一步也不麻烦，实际上就是对$J$求导，使得导数为$0$，即令$2{\sum }_{n=1}^N{r}_{nk}(x_n-{\mu }_k)=0$，解得${\mu }_k=\frac{{\sum }_n{r}_{nk}{x}_n}{{\sum }_n{r}_{nk}}$

1.3 实现技巧

在实现K-means的时候，也存在一些小技巧，比如说：

• 在初始化${\mu }_k$的时候，并不随机选择范围内的点，而是在已有的点中随机选择。
• 用不同的初始化结果多跑几次，选择其中效果最好的。
• 在E步骤中，需要计算$x_n$和${\mu }_k$之间的距离，那么这个时候可以使用KD-Tree等算法进行提速。（我没理解，总感觉直接计算时间复杂度更低，$O(kn)$嘛）
• 还可以使用Mini-batch K-Means。在每个E和M的迭代中，选择数据点中的一部分进行迭代。这样做是会更快，但是可能结果误差会更大。下面简单介绍一下：

当我们的Mini-batch选择为1的时候，就叫做Sequential Update，实际上就是对每一个数据点$x_n$进行操作，选择离它最近的中心点${\mu }_k^{old}$，对这个点进行更新：${\mu }_k^{new}={\mu }_k^{old}+{\eta }_n(x_n-{\mu }_k^{old})$。这种方法就比较适合数据点不是一下子全部得到的结果。Mini-batch更大的时候也是同样的道理。效果都是差不多的。

1.4 K-Mediods

有一种情况我们需要考虑，那就是如果这些数据点中存在噪声怎么办？就比如说下面图所示的数据点中最右边的那个点，很明显就是噪声，那么我们使用K-Means得到的中心点很明显不是我们想要的（如下图左边所示），这个时候就需要我们使用K-Mediods算法。

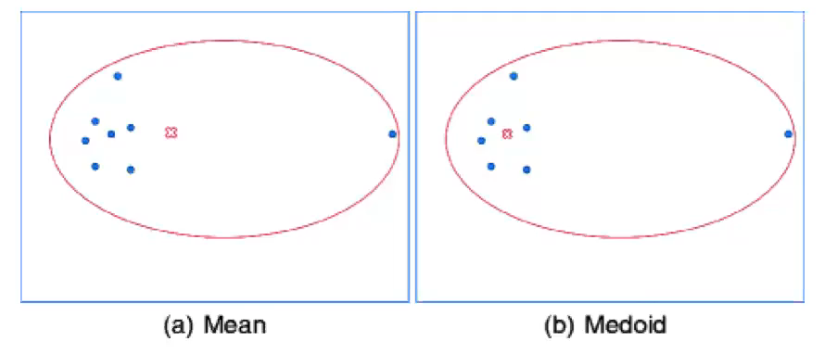
这个方法的E步骤和K-Means是一样的，但是M步骤有所不同，它所要最小化的函数并不是$J={\sum }_{n=1}^N{\sum }_{n=1}^K{r}_{nk}||x_n-{\mu }_k|{|}^2$了，而是$\tilde{J}={\sum }_{n=1}^N{\sum }_{n=1}^K{r}_{nk}v(x_n-{\mu }_k)$

其中的$v$函数是指一些并不能用数学方法具体表达的方法，在这里的$v$函数就是在这些数据点中选择一个点作为${\mu }_k$，然后其他点到这个点的距离之和。

也就是，这个算法的M步骤就是**选择这些数据点中的某个点作为中心点，要求其他店到这个中心点的距离和最小。**那么这个时候M步骤就不能用求导方法$O(1)$得到了，就只能逐个遍历了，最好情况下时间复杂度就变成了$O(k(n/k{)}^2)$

1.5 奇怪的应用：图片压缩

其实就是对图片的色彩进行压缩。每一个图片所占用的内存实际上是$H\ast W\ast RGB$，其中RGB是说照片的三原色，每一种颜色实际上都是要用8bit来进行表示，那么实际上占用的内存就是$H\ast W\ast 24$。但实际上，是不需要那么多颜色的，一般来说几种颜色就可以较好地表达完一张照片，比如说：

每一种颜色为一个类，那么存储空间就从$H\ast W\ast 24$变成了$H\ast W\ast K$，但由于每一个bit都可以用$2^M$，因此可以变成$H\ast W\ast lo{g}_{2}K$

1.6 局限性

K-Means主要存在两个方面的局限性：

• $K$的数值需要自己去定
• 每一个点不是这个类就是那个类，不能计算置信度

1.7 代码

from sklearn import datasets
import numpy as np
import open3d as o3d

n_sample = 500
noisy_moon = datasets.make_moons(n_samples=n_sample, noise=.05)
# print(noisy_moon[0])

def dis(a, b) :
    return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1])

def kmeans(data, k, tolerance, maxIter) :
    idx = np.random.choice(len(data), k, replace=False)
    centroids = data[idx]
    cluster = np.zeros(len(data))
    dist = np.zeros(len(data))
    for i in range(maxIter) :
        for j in range(len(data)) :
            cluster[j] = -1
            dist[j] = 1e10
        for j in range(len(data)) :
            for k in range(len(centroids)) :
                tmp = dis(data[j], centroids[k])
                if tmp < dist[j] :
                    dist[j] = tmp
                    cluster[j] = k

        old_centroids = np.copy(centroids)
        for j in range(len(centroids)) :
            dataTmp = data[cluster == j]
            if len(dataTmp) > 0 :
                centroids[j][0] = np.mean(dataTmp[:, 0])
                centroids[j][1] = np.mean(dataTmp[:, 1])
            else :
                centroids[j] = data[np.random.choice(len(data), 1, replace=False)]

        distortion = np.linalg.norm(centroids - old_centroids)
        if distortion < tolerance :
            break

    return cluster, centroids

# cluster, centroids = kmeans(noisy_moon[0], 2, 0.0001, 1000)
# print(cluster)
datas = np.zeros([len(noisy_moon[0]), 3])
for i in range(len(noisy_moon[0])) :
    datas[i][0] = noisy_moon[0][i][0]
    datas[i][1] = noisy_moon[0][i][1]
    datas[i][2] = 0
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(datas)

cluster, centroids = kmeans(datas, 2, 0.0001, 1000)
color = np.zeros([len(noisy_moon[0]), 3])
for i in range(len(noisy_moon[0])) :
    if cluster[i] == 0 :
        color[i][0] = 1
    else :
        color[i][1] = 1

pcd.colors = o3d.utility.Vector3dVector(color)

o3d.visualization.draw_geometries([pcd])

2 GMM

GMM实际上就是使用高斯模型去表示每一个类，使用这种方式就可以去计算每一个点属于各个类的置信度。

2.1 高斯模型

一维高斯模型为：

N ( x ∣ μ , σ 2 ) = 1 ( 2 π σ 2 ) e x p { − 1 2 σ 2 ( x − μ ) 2 } N(x|\mu, \sigma^2) = \frac{1}{(2\pi \sigma^2)}exp\{-\frac{1}{2\sigma^2}(x - \mu)^2\} N(x∣μ,σ2)=(2πσ2)1​exp{−2σ21​(x−μ)2}

而高维的高斯模型即为：

N ( x ∣ μ , Σ ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ ) T Σ ( − 1 ) ( x − μ ) } N(\mathbf{x}|\mathbf{\mu}, \mathbf{\Sigma}) = \frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp\{-\frac{1}{2}(\mathbf{x} - \mathbf{\mu})^T\mathbf{\Sigma}^{(-1)}(\mathbf{x} - \mathbf{\mu})\} N(x∣μ,Σ)=(2π)D/21​∣Σ∣1/21​exp{−21​(x−μ)TΣ(−1)(x−μ)}

2.2 GMM模型

实际上就是好多个高斯模型的线性组合。那么我们可以算出$x$点存在点的可能性为：

$p(x)={\sum }_{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$

其中，${\pi }_k$为第$k$个高斯模型所占的比重。因此，要描述一个GMM模型，所需要的参数就是 { μ k , Σ k , π k } , k = 1 , 2 , . . . , k \{\mu_k, \Sigma_k, \pi_k\}, k = 1, 2, ..., k {μk​,Σk​,πk​},k=1,2,...,k

但是我们知道$p(x)$是没有用的，我们并不是要生成点，而是已经有了很多点我们需要去进行聚类。

2.3 数学基础

首先，我们定义一个布尔类型的变量 z k ∈ { 0 , 1 } , ∑ k z k = 1 z_k \in \{0, 1\}, \sum_kz_k = 1 zk​∈{0,1},∑k​zk​=1，这个指的是一种事件，就是表示“这个点属于第$k$类”这个事件。

那么，$p(z_k=1)={\pi }_k$就是一种先验分布，等同于K-Means中的$r_{nk}$，不同的是他并不是说非$0$即$1$，而是说是存在概率的。那么，什么叫先验分布呢？就是说这个空间内任意存在一个点，咱也不知道这个点具体会在哪里，就是它属于哪一个高斯分布的概率。那我都完全不知道点在哪里，那只能通过权重来进行判断了不是嘛？它所占的比重越大，${\pi }_k$就越大。后验就是知道了高斯分布，也知道了$x$在哪里，求出$p(z|x)$，也就是这个点属于分布$z$的概率。

那么这个后验分布就可以用贝叶斯公式来进行计算：

$p(z|x)=\frac{p(x|z)p(z)}{p(x)},p(x)={\sum }_{z}p(z)p(x|z)$

其中，$p(z)$是先验分布，$p(x)$则是2.2节中所介绍的，$p(x|z)$就之后再介绍一下。

接下来需要介绍一种表示方法：

我们的$z_k=1$事件也可以表示为一种1-of-k的方法，也就是$z=[z_1,...,z_k,...,z_K]$，其中只有$z_k=1$，其他的为$0$。这样表示的话，我们之前所提到的先验分布$p(z_k=1)={\pi }_k$就表示为$p(z)={\Pi }_{k=1}^K{\pi }_k^{z_k}$。这也很好理解，毕竟其他值都是$0$，任何数的$0$次方都为$1$，因此就和没有乘是一样的效果。

上面一段的意思就是： $p(z_k=1)={\pi }_k$等同于$p(z)={\Pi }_{k=1}^K{\pi }_k^{z_k}$。

我们再来看$p(x|z_k=1)$，这个其实就坍塌成了一个普通的高斯分布，也就是$p(x|z_k=1)=N(x|{\mu }_k,{\Sigma }_k)$

再用上上面那一大段所描述的思想，是不是其实就是$p(x|z)={\Pi }_{k=1}^{K}N(x|{\mu }_k,{\Sigma }_k{)}^{z_k}$

然后，我们利用联合分布进行计算，也就是$p(x)={\sum }_{z}p(x,z)$，再利用全概率公式，即可得到：

$p(x)={\sum }_{z}p(z)p(x|z)={\sum }_{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$

这下我们就可以计算出后验分布$p(z|x)$咯，我们用$\gamma (z_k)$来表示$p(z_k=1|x)$，那么就会有：

$p(z|x)=\frac{p(z,x)}{p(x)}=\frac{p(z)p(x|z)}{{\sum }_{j=1}^{K}p(x|z_j)p(z_j)}$

$\gamma (z_k)\equiv p(z_k=1|x)=\frac{p(z_k=1)p(x|z_k=1)}{{\Sigma }_{j=1}^{K}p(x|z_j=1)p(z_j=1)}=\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}$

但是！虽然我们可以计算出每一个点分布给每一个高斯分布的概率，可是高斯分布的参数（$\mu ,\Sigma ,\pi$）完全没有去进行计算，上面过程是假设已经确定好了而已。那么，应该如何去进行计算呢？这个时候就要用到MLE算法了。

2.4 MLE(Maximum Likelihood)

2.4.1 奇点问题

假如说，有一个分布是一个圆形的，也就是${\Sigma }_k={\sigma }_k^{2}I$，然后这个点的位置就在这个分布的中心，也就是$x_n={\mu }_j$，那么就会有：

$N(x_n|x_n,{\sigma }_j^{2}I)=\frac{1}{(2\pi {)}^{1/2}\frac{1}{{\sigma }_j}}$

但如果${\sigma }_j$很小的话，这个值就会非常大，甚至会达到$\inf$，也就是说一个分布里面只有一个点的话就容易出现这种情况。那么该如何避免奇点问题呢？最好的解决方式就是不使用MLE，转而使用MAP或者贝叶斯接近。

但是那两种方法太过麻烦，因此可以在${\Sigma }_k$很小，就重新给它初始化一个很大的值就好了。

2.4.2 MLE的具体步骤

实际上这个过程就是要让各个分布能够很好的拟合点，实际上也就是最大化$p(x)$。

对于单个点来说，$p(x)={\sum }_{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$

最终目标是要每个点的$p(x)$连乘值最大，但是连乘是很难进行计算的，因此我们可以取对数，从而使得乘法变成加法：

ln ⁡ p ( X ∣ π , μ , Σ ) = ∑ n = 1 N ln ⁡ { ∑ k = 1 K π k N ( x n ∣ μ k , Σ k ) } \ln p(X|\pi, \mu, \Sigma) = \sum_{n = 1}^N\ln\{\sum_{k = 1}^K\pi_kN(x_n|\mu_k, \Sigma_k)\} lnp(X∣π,μ,Σ)=∑n=1N​ln{∑k=1K​πk​N(xn​∣μk​,Σk​)}，然后将其最大化。

有三个参数该怎么办呢？很简单，这三个每次都固定两个，然后变化其中的一个。具体步骤我们放在下面：

2.4.3 对${\mu }_k$进行操作

上面这一大串，我们首先对${\mu }_k$求导，让它等于$0$，结果就是：

$0=-{\sum }_{n=1}^N\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\Sigma }_j{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}{\sum }_k(x_n-{\mu }_k)$

我们注意到，中间这一大坨（$\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\Sigma }_j{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}$）是我们之前算的后验概率$\gamma (z_{nk})$，那么就可以将上面的公式简化为：

$0=-{\sum }_{n=1}^N\gamma (z_{nk}){\sum }_k(x_n-{\mu }_k)$

计算一下：

符号和${\Sigma }_k$都是可以去掉的：$0={\sum }_{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)$

${\sum }_{n=1}^N\gamma (z_{nk})x_n={\mu }_k{\sum }_{n=1}^N\gamma (z_{nk})$

${\mu }_k=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})x_n,N_k={\sum }_{n=1}^N\gamma (z_{nk})$

其中，$N_k$感性理解，实际上就是有多少个点属于第$k$类，就算后验概率为$0.5$，也就是有$50\%$的概率属于$k$，那也就可以算有$0.5$个点属于$k$。那么，实际上${\mu }_k$不就是每个点的加权平均嘛？

2.4.4 对${\Sigma }_k$进行操作

仍然是对${\Sigma }_k$进行求导，得到的结果为：

${\Sigma }_k=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T$

可以注意到，这个是对方差的加权平均。

2.4.5 对${\pi }_k$进行操作

针对${\pi }_k$，我们不能够像上面两个参数进行操作了，因为我们的${\pi }_k$是有约束条件的：

${\sum }_{k=1}^K{\pi }_k=1$

那么我们就要使用拉格朗日乘子法，也就是让原式子变成：

$\ln p(X|\pi ,\mu ,\Sigma )+\lambda ({\sum }_{k=1}^K{\pi }_k-1)$

然后对${\pi }_k$求导让它等于$0$：

$0={\sum }_{n=1}^N\frac{N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_k,{\Sigma }_k)}+\lambda$

两边同时乘以${\sum }_{k=1}^K{\pi }_k$，就会变成$0={\sum }_{n=1}^N{\sum }_{k=1}^K\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_k,{\Sigma }_k)}+{\sum }_{k=1}^K{\pi }_k\lambda$

把其中一个求和放到上面去，$0={\sum }_{n=1}^N\frac{{\sum }_{k=1}^K{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_k,{\Sigma }_k)}+{\sum }_{k=1}^K{\pi }_k\lambda$

就算字母不一样，但是分子分母还是一样的，就变成了$0=({\sum }_{n=1}^{N}1)+\lambda$，即$\lambda =N$

那就变成了$0={\sum }_{n=1}^N\frac{N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_k,{\Sigma }_k)}+N$

我们搞一个${\pi }_k$出来，变成$0=\frac{1}{{\pi }_k}{\sum }_{n=1}^N\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_k,{\Sigma }_k)}+N$

中间这一坨，又变成先验概率$\gamma (z_{nk})$咯，最后又成了$0=\frac{1}{{\pi }_k}{\sum }_{n=1}^N\gamma (z_{nk})-N$，结果就是简简单单的${\pi }_k=\frac{N_k}{N}$

2.5 总结算法

主要分为四步：

• 首先，初始化${\mu }_k,{\Sigma }_k,{\pi }_k$
• **E(expectation)步骤：**计算相应的后验概率$\gamma (z_k)=\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}$
• **M(maximization)步骤：**更新${\mu }_k,{\Sigma }_k,{\pi }_k$，即：
  • ${\mu }_k^{new}=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})x_n$
  • ${\Sigma }_k^{new}=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T$
  • ${\pi }_k^{new}=\frac{N_k}{N}$
  • $N_k={\sum }_{n=1}^N\gamma (z_{nk})$
• 然后计算 ln ⁡ p ( X ∣ π , μ , Σ ) = ∑ n = 1 N ln ⁡ { ∑ k = 1 K π k N ( x n ∣ μ k , Σ k ) } \ln p(X|\pi, \mu, \Sigma) = \sum_{n = 1}^N\ln\{\sum_{k = 1}^K\pi_kN(x_n|\mu_k, \Sigma_k)\} lnp(X∣π,μ,Σ)=∑n=1N​ln{∑k=1K​πk​N(xn​∣μk​,Σk​)}，收敛了即可停止

2.6 代码

from sklearn import datasets
import numpy as np
from scipy.stats import multivariate_normal
import open3d as o3d

n_sample = 500
noisy_moon = datasets.make_moons(n_samples=n_sample, noise=.05)
# da = datasets.make_circles(n_samples=n_sample, factor=.5, noise=.05)
data = noisy_moon[0]

def GMM(data, k, tolerance, maxIter):
    n, dim = data.shape
    mu = data[np.random.choice(range(n), k, replace=False)]
    var = np.array([np.eye(dim)] * k)
    w = np.ones([n, k]) / k
    pi = np.ones(k) / k
    nll = np.inf

    for j in range(maxIter):
        # E Step
        pdfs = np.zeros(((n, k)))
        for i in range(k):
            pdfs[:, i] = pi[i] * multivariate_normal.pdf(data, mean=mu[i], cov=np.diag(var[i]))

        w = pdfs / pdfs.sum(axis=1).reshape(-1, 1)

        # M Step
        # pi
        Nk = w.sum(axis=0)
        pi = Nk / Nk.sum()
        # mu
        for i in range(k):
            mu[i] = np.multiply(w[:, i].reshape(-1, 1), data).sum(axis=0) / Nk[i]
        # var
        for i in range(k):
            var[i] = np.average((data - mu[i]) ** 2, axis=0, weights=w[:, i])
        # nll
        last_nll = nll
        nll = np.sum(np.log(pdfs.sum(axis=0)))
        if np.abs(nll - last_nll) < tolerance:
            break
    return np.argmax(w, axis=1)

cluster = GMM(data, 2, 0.0001, 1000)
datas = np.zeros([len(noisy_moon[0]), 3])
for i in range(len(noisy_moon[0])) :
    datas[i][0] = noisy_moon[0][i][0]
    datas[i][1] = noisy_moon[0][i][1]
    datas[i][2] = 0
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(datas)

color = np.zeros([len(noisy_moon[0]), 3])
for i in range(len(noisy_moon[0])) :
    if cluster[i] == 0 :
        color[i][0] = 1
    else :
        color[i][1] = 1

pcd.colors = o3d.utility.Vector3dVector(color)

o3d.visualization.draw_geometries([pcd])

3 EM

在上面所介绍的两种聚类方法中，我们都用到了EM的思想。EM就是为了解决模型中的一些参数没有确定的情况，也就是为了解决诸如$p(X|\theta )$中$\theta$不确定的问题。EM的整体思路主要分为四步：

• 首先选定初始化参数${\theta }^{old}$
• **E(expectation)步骤：**计算后验概率$p(Z|X,{\theta }^{old})$
• **M(maximization)步骤：**求解优化问题来计算${\theta }^{new}$。
  • KaTeX parse error: Undefined control sequence: \Q at position 26: …w} = \arg \max \̲Q̲(\theta, \theta…
  • KaTeX parse error: Undefined control sequence: \Q at position 1: \̲Q̲(\theta, \theta…
• 检查是否收敛，如果不收敛重新回到E步骤。

3.1 用EM解决GMM问题

首先我们知道先验概率有$p(z)={\Pi }_{k=1}^K{\pi }_n^{z_k}$

以及$p(x|z)={\Pi }_{k=1}^{K}N(x|{\mu }_k,{\Sigma }_k{)}^{z_k}$

我们就可以计算出联合分布$p(X,Z|\mu ,\Sigma ,\pi )={\Pi }_{n=1}^N{\Pi }_{k=1}^{K}N(x_n|{\mu }_k,{\Sigma }_k{)}^{z_{nk}}$

迎合一下EM算法，取一下对数 ln ⁡ p ( X , Z ∣ μ , Σ , π ) = ∑ n = 1 N ∑ k = 1 K z n k { ln ⁡ π k + ln ⁡ N ( x n ∣ μ k , Σ k ) } \ln p(X, Z|\mu, \Sigma, \pi) = \sum_{n = 1}^N \sum_{k = 1}^Kz_{nk}\{\ln \pi_k + \ln N(x_n|\mu_k, \Sigma_k)\} lnp(X,Z∣μ,Σ,π)=∑n=1N​∑k=1K​znk​{lnπk​+lnN(xn​∣μk​,Σk​)}

我们要求的是KaTeX parse error: Undefined control sequence: \Q at position 1: \̲Q̲(\theta, \theta…，那我们就要在对数结果的基础上求一下期望。我们注意到，在$\ln p(X,Z|\mu ,\Sigma ,\pi )$中，后面大括号里面的东西都和$z$没有关系，所以：

E z [ ln ⁡ p ( X , Z ∣ μ , Σ , π ) ] = ∑ n = 1 N ∑ k = 1 K E [ z n k ] { ln ⁡ π k + ln ⁡ N ( x n ∣ μ k , Σ k ) } E_z[\ln p(X, Z|\mu, \Sigma, \pi)] = \sum_{n = 1}^N \sum_{k = 1}^KE[z_{nk}]\{\ln \pi_k + \ln N(x_n|\mu_k, \Sigma_k)\} Ez​[lnp(X,Z∣μ,Σ,π)]=∑n=1N​∑k=1K​E[znk​]{lnπk​+lnN(xn​∣μk​,Σk​)}

而我们的$z_{nk}$只有等于$0$和等于$1$两种情况，我们再看一下我们之前所计算的后验概率：

$\gamma (z_k)\equiv p(z_k=1|x)=\frac{p(z_k=1)p(x|z_k=1)}{{\Sigma }_{j=1}^{K}p(x|z_j=1)p(z_j=1)}=\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}$

所以实际上$E[z_{nk}]=0\ast p(z_{nk}=0|x_n,{\mu }_k,{\Sigma }_k,{\pi }_k)+1\ast p(z_{nk}=1|x_n,{\mu }_k,{\Sigma }_k,{\pi }_k)=\gamma (z_{nk})$

我们最后的KaTeX parse error: Undefined control sequence: \Q at position 1: \̲Q̲函数就是 Q = E z [ ln ⁡ p ( X , Z ∣ μ , Σ , π ) ] = ∑ n = 1 N ∑ k = 1 K γ ( z n k ) { ln ⁡ π k + ln ⁡ N ( x n ∣ μ k , Σ k ) } Q = E_z[\ln p(X, Z|\mu, \Sigma, \pi)] = \sum_{n = 1}^N \sum_{k = 1}^K\gamma(z_{nk})\{\ln \pi_k + \ln N(x_n|\mu_k, \Sigma_k)\} Q=Ez​[lnp(X,Z∣μ,Σ,π)]=∑n=1N​∑k=1K​γ(znk​){lnπk​+lnN(xn​∣μk​,Σk​)}

解出来的结果和直接求是一样的：

• ${\mu }_k^{new}=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})x_n$
• ${\Sigma }_k^{new}=\frac{1}{N_k}{\sum }_{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T$
• ${\pi }_k^{new}=\frac{N_k}{N}$

3.2 K-Means再认识

K-Means实际上就是一种特殊的GMM！

• GMM中的$\gamma (z_{nk})$实际上就是K-Means中的$r_{nk}$
• K-Means就是${\Sigma }_k=0$的GMM

证明一下：

我们有$\gamma (z_k)\equiv p(z_k=1|x)=\frac{p(z_k=1)p(x|z_k=1)}{{\Sigma }_{j=1}^{K}p(x|z_j=1)p(z_j=1)}=\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)}$

在K-Means中，我们认为它的分布都是圆形的，也就是各个方向都是相等的，即${\Sigma }_k=ϵI$

也就是说 p ( x ∣ μ k , Σ k ) = 1 ( 2 π ϵ ) 1 / 2 e x p { − 1 2 ϵ ∣ ∣ x − μ k ∣ ∣ 2 } p(x|\mu_k, \Sigma_k) = \frac{1}{(2\pi\epsilon)^{1/2}}exp\{-\frac{1}{2\epsilon}||x - \mu_k||^2\} p(x∣μk​,Σk​)=(2πϵ)1/21​exp{−2ϵ1​∣∣x−μk​∣∣2}

稍微结合一下，就会有在K-Means情况下：

γ ( z n k ) = π k e x p { − ∣ ∣ x n − μ k ∣ ∣ 2 / 2 ϵ } ∑ j π j e x p { − ∣ ∣ x n − μ j ∣ ∣ 2 / 2 ϵ } \gamma(z_{nk}) = \frac{\pi_kexp\{-||x_n - \mu_k||^2 / 2\epsilon\}}{\sum_j\pi_jexp\{-||x_n - \mu_j||^2 / 2\epsilon\}} γ(znk​)=∑j​πj​exp{−∣∣xn​−μj​∣∣2/2ϵ}πk​exp{−∣∣xn​−μk​∣∣2/2ϵ}​

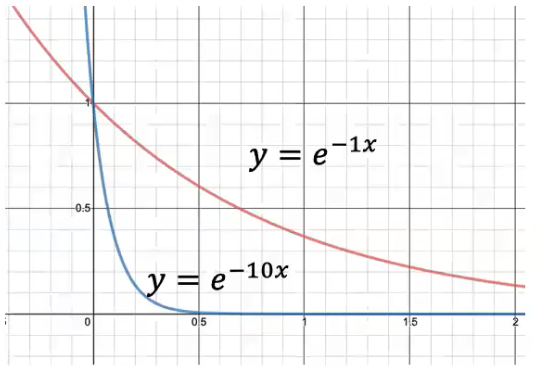
可以看到，exp函数的系数越大，就下降的越快，而$ϵ$又十分接近$0$，因此系数应该是无限大的，也就是说这个函数下降的贼快，不是$0$就是无穷大。那么我们用$j\ast$来表示接近的类。只有当$j=j\ast andk=j\ast$是，才为$1$。因此，这个函数就坍塌为了$r_{nk}$

因此带入KaTeX parse error: Undefined control sequence: \Q at position 1: \̲Q̲函数中，得到： Q = E z [ ln ⁡ p ( X , Z ∣ μ , Σ , π ) ] = ∑ n = 1 N ∑ k = 1 K r n k { ln ⁡ π k + ln ⁡ N ( x n ∣ μ k , Σ k ) } Q = E_z[\ln p(X, Z|\mu, \Sigma, \pi)] = \sum_{n = 1}^N \sum_{k = 1}^Kr_{nk}\{\ln \pi_k + \ln N(x_n|\mu_k, \Sigma_k)\} Q=Ez​[lnp(X,Z∣μ,Σ,π)]=∑n=1N​∑k=1K​rnk​{lnπk​+lnN(xn​∣μk​,Σk​)}

又因为我们有${\Sigma }_k=ϵI,ϵ\to 0$

于是就变成了$Q=E_z[\ln p(X,Z|\mu ,\Sigma ,\pi )]=-\frac{1}{2}{\sum }_{n=1}^N{\sum }_{k=1}^K{r}_{nk}||x_n-{\mu }_k|{|}^2+const$

里面的常数就是${\pi }_k$乘出来的一坨，没啥用。这样的话实际上就和我们学习K-Means中的$J$函数长的一样啦。证明完毕。