【实验报告】【概率论与数理统计】原神双卡池下的月卡玩家抽卡策略分析

一、问题概述和分析

（1）问题描述

《原神》是一款开放世界游戏，其中玩家可以操控各种各样的角色游玩。角色分为四星以及五星两种，角色的获取通过抽卡获得。抽卡需要消耗玩家所持的原石，每160原石可以兑换一次抽卡机会。具体的抽卡规则如下：
《原神》在2.3版本中开放双卡池模式，官方公布规则如下：
注：以下规则的叙述均以2.4版本中阿贝多卡池为例，对于其余卡池规则一致

“在本期「深秘之息-活动祈愿」中5星角色祈愿的基础概率为0.600%,综合概率(含保底)为1.600%,最多90次祈愿必定能通过保底获取5星角色。
当祈愿获取到5星角色时,有50.000%的概率为本期5星 UP 角色「白垩之子·阿贝多(岩)」。如果本次祈愿获取的5星角色非本期5星 UP 角色，下次祈愿获取的5星角色必定为本期5星 UP 角色。
在本期「深秘之息」活动祈愿中,4星物品祈愿的基础概率为5.100%,4星角色祈愿的基础概率为2.550%,4星武器祈愿的基础概率为2.550%,4星物品祈愿的综合概率(含保底)为13.000%。最多10次祈愿必定能通过保底获取4星或以上物品,通过保底获取4星物品的概率为99.400%,获取5星物品的概率为0.600%。
当祈愿获取到4星物品时,有50.000%的概率为本期4星 UP 角色「命运试金石·班尼特(火)」、「未授勋之花-诺艾尔(岩)」、「棘冠恩典·罗莎莉亚(冰)」中的一个。如果本次祈愿获取的4星物品非本期4星 UP 角色,下次祈愿获取的4星物品必定为本期4星 UP 角色。当祈愿获取到4星 UP 物品时,每个本期4星 UP 角色的获取概率均等。
「角色活动祈愿」和「角色活动祈愿-2」共享保底抽数。”

双卡池意味着一次即将复刻两名角色。在这样的情况下，角色复刻 速度加快，导致部分玩家必须在两个卡池之间做出选择。不同玩家的抽卡需求不同，手中掌握的原石 数目也不同，不仅如此，上个卡池的抽数也会对本卡池的抽卡决策造成一定程度的影响，因此抽卡决策变得复杂而多样。在原神的玩家中，零氪玩家 和月卡玩家 占比重最大，而相较于中氪玩家和重氪玩家，零氪玩家和月卡玩家原石数目更加有限，对于抽卡策略的选取上也更加谨慎，对于合理化的抽卡策略需求量较大。

（2）问题分析

零氪玩家和月卡玩家是单向转化关系。从基数上来看，零氪玩家和月卡玩家所占比重都较大；但从两者关系上来看，零氪玩家和月卡玩家之间并不是相互独立的，而是单向转化的关系，零氪玩家可以转化为月卡玩家，而反过来却行不通。可以预料的，在玩家总数一定时，月卡玩家的数量是会不断增加的。因此，将月卡玩家作为研究主体的实际意义更大，未来的受众面也更广。故将月卡玩家作为研究主体。（若无特殊说明，下文中的“用户”均代指“月卡玩家”）

双卡池的本质依旧是单个卡池在抽数共享情况下的复数叠加，所以本文将解决问题的步骤分为：1、研究单个卡池中五星、四星的抽卡机制。
2、研究双卡池机制对用户决策的影响。
3、引入“前一卡池抽卡数目”、“用户对四星以及五星需求”、“用户拥有原石数目”、“整个版本活动获得原石数目”等因素综合考虑抽卡策略。
4、得出不同情况下用户的相对最佳抽卡策略。

（3）实验目的

针对月卡玩家，借助概率论知识，通过对卡池概率的研究，得到将“前一卡池抽卡数目”、“用户对四星以及五星需求”、“用户拥有原石数目”、“整个版本活动获得原石数目”纳入考虑的相对最佳抽卡策略。

二、实验设计总体思路

2.1、引论（本门课程与实验的相关内容）

1）问题假设
1、假设原神玩家总数不变。
2、假设未推出的卡池对本研究没有影响，即未推出的卡池对于用户的抽取选择无影响。
3、假设用户将本卡池抽出相应角色作为第一要义，如果不能达到一定的概率，则本卡池放弃抽取。即不考虑用户“垫抽数” 的情况存在。
4、假设用户对于四星的需求仅限于0命和6命 ，并且6命之后的重复抽取视为无效。
5、假设抽卡过程中仅出现角色，不出现武器。也就是说不考虑武器的抽取概率，本文所提到的“五星”、“四星”仅仅代指角色星级。
6、用户手中的原石仅用于抽取限定角色卡池。
7、在抽取四星时假设五星对其无影响，也就是说，五星和四星不耦合。

2）符号解释

2.2、实验主题部分

2.2.1、实验设计思路

1 理论分析

1.1五星抽取分析

设随机事件$A_i$为第i次抽卡抽到五星，本文将官方给出的规则“5星角色祈愿的基础概率为0.600%,综合概率(含保底)为1.600%,最多90次祈愿必定能通过保底获取5星角色”中的“综合概率” $P(C)$理解为
$$\mathrm{P}(\mathrm{C})=\frac{1}{\text{抽出五星所需要的平均抽数}}\text{ 式(1)}$$
即抽出五星的平均概率。

1.1.1朴素的经验概率理解

官方说“最多90次祈愿必定能通过保底获取5星角色”，故可以知道$\mathrm{P}({\mathrm{A}}_{90})=1,P(C||B_{90})=1,$再加之“5星角色祈愿的基础概率为0.600%”，故$P(\mathcal{C}||\overline{B_{90}})=0.006,$，将前89抽看作相互独立的p=0.006的伯努利分布，可以得到如下概率模型：

$$\mathrm{P}(A_i)=\{\begin{array}{c}0.006,0<\mathrm{i}<90\\ 1,\mathrm{i}=90\end{array}\text{式(2)}$$
由上述概率模型列出全概率公式：
$$\{\begin{array}{c}P(B_{90})P(C||B_{90})+P(\overline{B_{90}})P(C||\overline{B_{90}})=P(C)\\ P(C){\prod }_{i=1}^{89}[1-P(A_i)]=P(B_{90})\end{array}\text{式(3)}$$
求得$P(C)’=0.01435$，与官方给出的0.016差距较大。

1.1.2改进的经验概率理解

在不怀疑官方给出的P©和基础概率的情况下，类比米哈游 之前推出的游戏如崩坏三等的抽卡机制，推断同一家游戏公司所推出的游戏抽卡概率机制应当基本相同，概率很有可能从某一次抽数开始线性增加，直至90抽时抽出五星的概率达到100%，并且在概率线性增加之前抽出五星的概率仍然为0.6%。
设概率从第x抽开始改变，综合概率$P(C)=1.6\%$，则可以得到如下的概率模型：
$$\text{P(A i)}=\{\begin{array}{l}0.006,0<\mathrm{i}\le \mathrm{x}\\ \frac{1-0.006}{90-\mathrm{x}}\left(\mathrm{i}-\mathrm{x}\right)+0.006,\mathrm{x}<\mathrm{i}<90\\ 1,\mathrm{i}=90\end{array}\text{式(4)}$$
计算可得到x=73，所以概率模型为：
$$\text{P(A i)}=\{\begin{array}{l}0.006,0<\mathrm{i}\le 73\\ \frac{1-0.006}{90-73}(\mathrm{i}-73)+0.006,73<\mathrm{i}<90\text{式(5})\\ 1,\mathrm{i}=90\end{array}$$
显然$A_i(i=1,2,\mathrm{3...90})$是相互独立的，概率不受彼此的影响。
对于事件第i次抽卡第一次抽到五星B_i来说。
$$\mathrm{P}({\mathrm{B}}_{\mathrm{i}})=\mathrm{P}({\mathrm{A}}_{\mathrm{i}}\overline{{\mathrm{A}}_1{\mathrm{A}}_2{\mathrm{A}}_3}...\overline{{\mathrm{A}}_{\mathrm{ı}-1}})\text{ 式(5)}$$
又因为$A_i(i=1,2,\mathrm{3...90})$是相互独立的，所以式（5）可转化为
$$\mathrm{P}({\mathrm{B}}_{\mathrm{i}})=\mathrm{P}({\mathrm{A}}_{\mathrm{i}}\overline{{\mathrm{A}}_1{\mathrm{A}}_2{\mathrm{A}}_3...{\mathrm{A}}_{\mathrm{i}-1}})=\mathrm{P}({\mathrm{A}}_{\mathrm{i}})\prod _{\mathrm{j}=1}^{\mathrm{i}-1}\mathrm{P}({\mathrm{A}}_{\mathrm{j}})\text{式(6)}$$
联立式（6）和式（5）可以解出B_i的概率分布如下图：

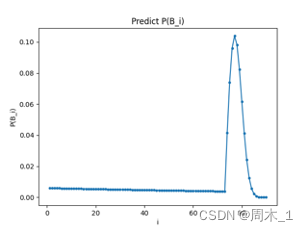
图 1 根据概率模型对$P(B_i)$的估计

$73\le i\le 90具体数据$
可以看出，抽到五星的概率在77抽时达到了最大，在区间74～80之间，抽到五星的概率高达55.766%，已经超过50%。因此在一个卡池时间期间内将抽数抽到74～80之间是比较理想的状态。

1.1.3概率模型可靠性印证

为了印证在1.1.2中得到概率模型的可靠性，本文从网络 以及身边玩家收集了大量抽卡数据，将实际第一次出五星的概率与估计值对比如下：

图 2 预测数据与实际数据对比图
可以看到，实际数据与预测数据在大体走势上基本相同，尤其在74～90之间拟合效果良好，由此可以证明1.1.2的关于概率线性递增的猜想正确。
此外，在1～73，实际数据波动较大，但基本围绕预测值上下波动，且波动范围不大，基本保持在预测值附近，经过分析，认为是由于收据数据时的幸存者偏差 导致。
所以，1.1.2推出的关于五星抽卡的概率模型具有比较强的可靠性。

1.2四星抽取分析

官方给出的规则中提及“在本期「深秘之息」活动祈愿中,4星物品祈愿的基础概率为5.100%,4星角色祈愿的基础概率为2.550%,4星武器祈愿的基础概率为2.550%,4星物品祈愿的综合概率(含保底)为13.000%。最多10次祈愿必定能通过保底获取4星或以上物品,通过保底获取4星物品的概率为99.400%”，故也可得到朴素的经验概率模型，同1.1.1一致，和官方给出的综合概率差距较大，故舍弃。
经过分析猜想，四星抽取机制应当与五星抽取机制基本一致，故猜想：四星抽取在10抽之内的某一抽开始概率开始线性上升，直至第10抽概率达到99.400%。此处概率没有达到100%，是因为四星和五星的抽取并不是相互独立的，而是相互耦合的，所以第10抽也有可能抽出五星。这一点对于前9抽也是一样的道理。
基于网上资料结果，实际情况中四星的抽取几率如下：

首先，针对存在11抽出四星的概率同上文说的一样，第10抽抽出五星，将四星挤到第11抽。但满足“前9抽未出四星，第10抽出五星”的概率极小，尤其是针对个体用户（抽取数目有限，基数不大）来说，考虑四星、五星耦合的实际意义不大，故本文不考虑四星和五星耦合问题。
其次，可以明显的看出第9抽的时候概率大大提高，因此猜想上文提及的概率提高抽数为第9抽。因为是线性增加，可以计算出$P(D_9)=0.4715$，所以可以计算出$E_i$的概率：

由上述结果计算出的综合概率是12.99%，和官方给出的13%基本一致。

图 3 真实数据与预测数据对比图
但和实际情况下的抽取概率相比仍有一定的差距，由于数据统计时没有进行降噪处理，并且如果按照实际情况下的概率进行计算，最终的综合概率是大于官方给出的13%。经过综合考虑，此处相信官方给出的综合概率，故该概率模型比较可靠。

2.用户抽卡策略

根据用户抽卡的情况和需求不同，设N为用户在本次卡池开始时所已经抽取的数目$(0<N<90)$，M为用户在本次开始开始时所拥有的原石数目，$\beta$为用户对达到自己目的所能接受的最小概率。

2.1用户需求分类

在抽取五星方面上，如果用户目的为抽取某特定五星，用户只需要将所有的原石投入目标卡池，这种情况过于简单，所以不再考虑。故在抽取五星上，假设用户的目的是抽取尽可能多的五星，从而在概率上推得怎样分配原石可以获得最大的收益。
在抽取四星方面上，绝大多数用户都会遇到“只想抽取四星，不想抽取五星”的情况。但是抽取6命四星的情况下五星的概率不断叠加，最终很有可能会抽出五星；就算是只抽0命，如果上个卡池结束时抽数过多，也是有抽出五星的风险的。所以，相较于抽取尽可能多数目的五星，此种情况更加复杂，故将其作为一种单独分类。
经过以上分析将用户分为A用户、B用户两类：
A用户：以抽到尽可能多的五星作为目标。
B用户：以不抽取五星并且抽取0命四星作为目标。
C用户：以不抽取五星并且抽取6命四星作为目标。

2.2双卡池机制

2.2.1双卡池机制对概率的影响

官方规则中给出“「角色活动祈愿」和「角色活动祈愿-2」共享保底抽数。”，
从概率方面来看，双卡池只是卡池内五星改变，对于抽出五星本身的概率是没有任何影响的，也就是说上述在单卡池中讨论的结论，在遵循“「角色活动祈愿」和「角色活动祈愿-2」共享保底抽数。”的前提下，在双卡池机制下仍然适用。

2.2.2双卡池对用户抽取决策的影响

从五星方面来说，由于双卡池的抽数是共享的，在一个卡池内抽出五星也会导致另一卡池的抽数置零，所以忽略池内五星的差异，两者在本质上并没用任何区别。从四星角度来看，本次版本的双卡池都是复刻卡池，内部的四星配置完全相同，所以对于四星两个卡池是完全相同的。
从上述分析可知，在双卡池情况下的抽取策略制定和单个卡池并无本质区别，如果将单卡池的抽取策略制定出来，双卡池的策略也是相同的。所以在下文中，本文只讨论对单个卡池的五星、四星抽取策略。

2.3参数分析

对于用户在本次开始开始时所拥有的原石数目M，在本文的假设下，用户要么将自己的全部原石在本卡池使用完毕，要么不进行任何抽取活动。因此，我们合理推测用户在本卡池开始之前的卡池没有任何抽取行为。下面是对用户在一次卡池期间的原石获得途径统计分析：
在活动奖励原石中，每个版本为期40天，每个版本活动奖励原石数目有所不同，但基本稳定在2000原石左右，每个版本又被两个卡池均匀分开，故每个卡池期间的活动奖励原石数目估计为1000。
在深境螺旋中，获得原石的数目与用户的练度 有关，在此处合理推算用户可以将11层通至8星，所以获得原石数目为150×2+100=400。
在月卡每日登陆游戏和每日委托任务中，假设用户每天都登陆游戏并且完成每天的委托任务。
此外，并不考虑宝箱、神樱、世界等级提高、神像等级提升等一次性奖励。则总结出以下表格：

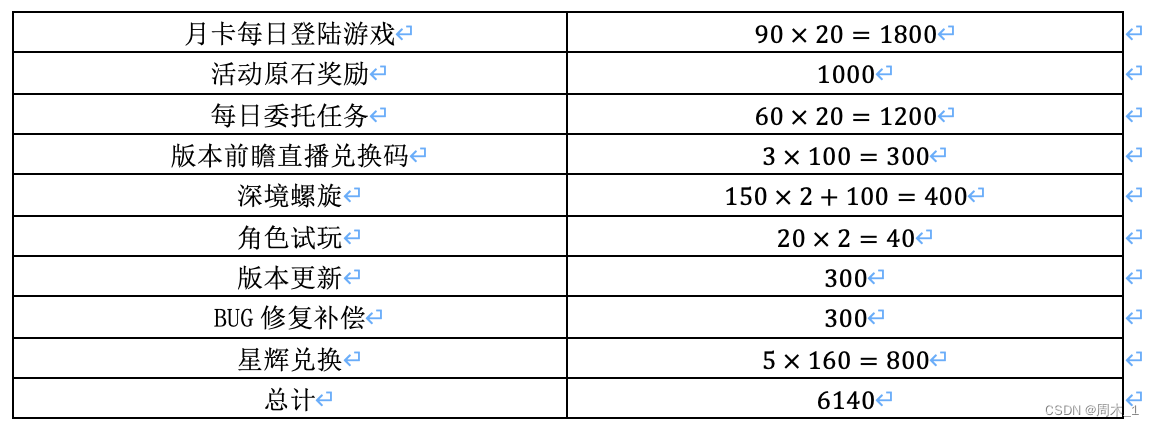
一卡池期间内用户获得原石数目统计表
由此合理推测出$M=6140$，换算为抽数为$6140÷160=38.375$，约为38抽 ，记为m。
用户对达到自己目的所能接受的最小概率$\beta$在此处估计为60%。

2.4五星抽卡策略（针对用户A的抽卡策略）

分析可以得知，前N抽属于原本就拥有的抽数，对于$P_1$没有任何影响，而在第N抽至第$N+m$抽之间的每一抽出金的概率是相互独立的，那么就可以类比计算$P(B_i)$的方式计算$P_1$，也就是说：
$$P_1=\{\begin{array}{c}{\sum }_{i=N+1}^{N+m}(P(A_i)\times {\prod }_{j=N+1}^{i-1}(1-P(A_j))),N+m<90\\ 1,N+m>=90\end{array}\text{式(7)}$$
由此编程计算得出$P_1$的分布：

图 4 对P1的预测概率

部分详细数据
由此可以看出，如果用户将自己在前一卡池所攒的原石完全用于抽取五星，那么在区间$0<N<37$中，概率基本维持在20%左右；$37\le N<44$抽到五星的概率极大增加；$44\le N$之后增长比较缓慢，并且逐渐趋近于100%。
结合$\beta$分析后，制定用户A的抽卡策略如下：
如果卡池抽数N大于40，则抽取；反之则不抽取。

2.5四星抽卡策略

2.5.1针对用户C的抽卡策略

“当祈愿获取到4星物品时,有50.000%的概率为本期4星 UP 角色「命运试金石·班尼特(火)」、「未授勋之花-诺艾尔(岩)」、「棘冠恩典·罗莎莉亚(冰)」中的一个。如果本次祈愿获取的4星物品非本期4星 UP 角色,下次祈愿获取的4星物品必定为本期4星 UP 角色。当祈愿获取到4星 UP 物品时,每个本期4星 UP 角色的获取概率均等。”根据官方给出的抽卡规则以及上文分析出的抽数m=38，显然可以推出获得6命某个特定的四星的概率极低，没有实际意义。也就是说用户C几乎不可能达到自己的目的。

2.5.2针对用户B的抽卡策略

简单分析可知，当研究多个四星抽取时，简单的将每次抽取看作独立事件在m=38的数量级下，导致的情况十分庞大，难以全部分析。所以，此处采取程序模拟抽取，当模拟次数足够大时，由大数定理可知，此时频率便趋近于概率。
$$P_2=P(\text{不抽出五星})\times P(\text{抽出一个目标四星的概率)}$$
此处的“不抽出五星”的概率不仅仅是等于上述P_1的取反，从实际情况考虑，如果用户已经抽出了目标四星那么用户就不需要继续抽取，所以此时抽取的抽数会发生变化，上述式（7）中的m值是实时改变的。所以这里的m值规定为，用户B达到目的所消耗的平均抽数。
将模拟抽取次数r定为1000000，其中用户B达到目的737218次，平均达到目的消耗抽数18.93，结合2.4五星抽卡策略，可以作出下图：

图 5 预测P2图线

部分具体数据
由此可以看出，在区间$0<N<57$中，概率基本维持在66%左右；$57\le N<64$达成目的的概率快速减小；$64\le N$之后减小比较缓慢，并且逐渐趋近于0%。
结合β分析后，制定用户B的抽卡策略如下：
如果卡池抽数N小于57，则抽取；反之，则很有可能在抽取过程中抽到五星触发保底清零机制，故不建议抽取。

实验主体部分到此为止，下面是实验报告的一些流程

2 实现方法（写清实验步骤及其依据）
五星抽取机制P(A_i)的分析主要是根据官方所给资料以及合理假设推出，然后格局各个事件之间逻辑关系，编程求解最终的在第i抽为第一次抽出五星的概率P(B_i)，并且绘出不同N情况下的概率图线。
四星抽取机制P(D_i)和P(E_i)和五星抽取机制思路基本相同，此处不再赘述。
用户A的抽取策略和推导P(B_i)的过程基本相同。
用户B的抽取策略由于四星每10发必出，所以导致可能情况不断增长，最终导致其无法分析。所以采用编程模拟抽卡，根据大数定理，最终得到的频率基本趋近于概率。
注：以上方法采用代码均在下面贴出。

2.2.2、实验结果及分析

具体的分析与采取公示均在理论分析中写出，下面为了直观可靠，仅展示得到的图线。

根据概率模型求解出$P(B_i)$

预测数据与实际数据对比图


对$P_1$的预测概率

预测$P_2$图线

2.2.3、程序及其说明

注：若无特殊说明本文采取代码均为Python
关于计算P(A_i)的函数：

def PA_i(i):
    if 0 < i and i < 74:
        return 0.006
    elif i < 90:
        return ((1-0.006)/(90-73))*(i-73)+0.006
    else:
        return 1

关于计算$P(B_i)$并且绘制真实数据与预测数据对比图函数：

def function3():
    PB_x = []
    x = []
    standar = [0.00828625, 0.01092279 ,0.00451977 ,0.00753296 ,0.00414313 ,0.01280603,
             0.00640301 ,0.00564972 ,0.00828625 ,0.0086629  ,0.00564972 ,0.00640301,
             0.00677966 ,0.00715631 ,0.00564972 ,0.00414313 ,0.00828625 ,0.00602637,
             0.00640301 ,0.00677966 ,0.00414313 ,0.00677966 ,0.00753296 ,0.00414313,
             0.00715631 ,0.00414313 ,0.00376648 ,0.00263653 ,0.00489642 ,0.00527307,
             0.0079096  ,0.00715631 ,0.00602637 ,0.00414313 ,0.00414313 ,0.00715631,
             0.00225989 ,0.00640301 ,0.00414313 ,0.00489642 ,0.00414313 ,0.00527307,
             0.00301318 ,0.00338983 ,0.00677966 ,0.00301318 ,0.00564972 ,0.00225989,
             0.00451977 ,0.00451977 ,0.00376648 ,0.00602637 ,0.00489642 ,0.00338983,
             0.00376648 ,0.00338983 ,0.00301318 ,0.00489642 ,0.00527307 ,0.00527307,
             0.00225989 ,0.00414313 ,0.00338983 ,0.00301318 ,0.00451977 ,0.00564972,
             0.00414313 ,0.00188324 ,0.00301318 ,0.00451977 ,0.00451977 ,0.00301318,
             0.00225989 ,0.03917137 ,0.07457627 ,0.09943503 ,0.10207156 ,0.0960452,
             0.08060264 ,0.05725047 ,0.03427495 ,0.02109228 ,0.0094162  ,0.00489642,
             0.00263653 ,0.         ,0.0007533  ,0.         ,0.         ,0.        ]
    for i in range(1, 91):
        temp = 1
        for j in range(1, i):
            temp *= (1 - PA_i(j))
        temp *= PA_i(i)
        PB_x.append(temp)
        x.append(i)
#        print("P(B"+str(i)+")=%.6f"%(temp*100))
    print(PB_x)
    plt.plot(x, PB_x, '.b-', label="expect line")
    plt.plot(x, standar, 'r-', label="real line")
    plt.title("Predict P(B_i)")
    plt.xlabel("i")
    plt.ylabel("P(B_i)")
    plt.legend(loc = 'upper left')
    plt.show()

关于计算$P(D_i)$的函数:

def PD_i(i):
    if i == 9:
        return 0.4715
    elif i == 10:
        return 0.994
    else:
        return 0.051

关于计算$P(E_i)$并且绘制真实数据与预测数据对比图函数：

def function1(count):
    PE = []
    standar=[0.0535, 0.0471, 0.0488, 0.0430 ,0.0379, 0.0381, 0.0344, 0.0346, 0.3714, 0.2875, 0.0037]
    for i in range(1, count+1):
        temp = 1
        
        for j in range(1, i):
            temp *= (1-PD_i(j))
        temp *= PD_i(i)
        print("P(E"+str(i)+")="+str(temp))
        PE.append(temp)
    
    plt.plot(range(1, 11), PE, '.b-', label="expect line")
    plt.plot(range(1, 12), standar, 'r-', label="real line")
    plt.title("Predict P(E_i)")
    plt.xlabel("i");
    plt.ylabel("P(E_i)");
    plt.legend(loc = 'upper left')
    plt.show()

关于计算$P_1$并且绘制图线函数：

def function2():
    P1 = []
    for N in range(0, 90):
        temp1 = 0
        if N+m <90:
            for i in range(N+1, N+m):
                temp2 = 1
                for j in range(N+1, i):
                    temp2 *= (1 - PA_i(j))
                temp2 *= PA_i(i)
                temp1 += temp2
        else:
            temp1 = 1
        P1.append(temp1)
    
    plt.plot(range(0, 90) ,P1, '.b-')
    plt.xlabel("N")
    plt.ylabel("P1")
    plt.title("Predict P1")
    plt.show()
    for i in range(0, 90):
        print("**"+str(i)+"** "+str(P1[i]))

关于模拟四星抽卡的函数：

def function1():
    global countNumber
    global countSuccess
    count = 0 #记录当前多少抽未四星
    flag = False #记录当前抽出的四星是不是大保底
    for i in range(1, maxM):
        count += 1
        if myRandom(PD_i(count)): #是否抽出四星
            count = 0 #抽出四星count归零
            if flag: #是否是大保底
                if myRandom(1/3): #判断是不是自己想要的四星（大保底）
                    countSuccess += 1
                    countNumber.append(i)
                    break
            elif myRandom(0.5): #判断是不是up四星
                if myRandom(1/3): #判断是不是自己想要的四星（已经确认是up四星）
                    countSuccess += 1
                    countNumber.append(i)
                    break
            else: #如果不是大保底，并且不是up四星，所以触发大保底机制
                flag = True

关于计算$P_2$的代码：

for o in range(0, countRange):
    if o%1000 == 0:
        print(o)
    function1()

P1_m = P1( int( (np.sum(countNumber))/countSuccess ))
for j in range(0, 90):
    P2.append( ( (1-P1_m[j]) * (countSuccess/countRange) ) )
plt.plot(range(0, 90) ,P2, '.b-')
plt.xlabel("N")
plt.ylabel("P2")
plt.title("Predict P2")
plt.show()
for i in range(0, 90):
    print("**"+str(i)+"**="+str(P2[i]))

2.3、对教材正文的深入理解和创新性说明

该实验在没有任何模型的情况下依靠官方给出规则说明以及网络收集真实数据，进行合理假设，最终得到了针对不同用户需求的抽卡方案。本文的抽卡事件可以看成复数个伯努利分布由于某中国特殊的规则组合在一起，分析该问题让我在思考复杂概率模型以及如何进行合理的数学建模方面有了更深的理解。在思考各个事件的逻辑关系以及其概率关系时，我深刻的体会到自己在处理复杂关系的短板。

2.4、体会

本文的概率模型从结果上来看并不算复杂，但是根据实际情况推导的过程却异常艰难。一方面要考虑诸多因素让模型更加符合实际情况，否则得到的模型没有现实意义；一方面需要合理的简化模型，否则模型过于复杂，无法求解出最终的结果。
在思考各个事件的逻辑关系以及其概率关系时，我深刻的体会到自己在处理复杂关系的短板。但面对较大的计算规模，人力无法求解，编程思想的实际应用也让我受益匪浅。
缺点：在求解用户B的抽取策略时，由于无法求解复杂的模型，也找不到特殊的方法对其进行简化，最终只能采取虚拟抽卡求解用户B达到目的的概率与平均抽数。