PEP:Pessimistic Error Pruning
本文分为两部分:
第一部分:1986年的PEP剪枝算法原理
第二部分:1997年的PEP剪枝算法原理以及与前者的对比
-----------------------------
第一部分:
《Simplifying Decision Trees》-1986
作者:J.R. Quinlan
该论文的2.3 Pessimistic Pruning 首次提出了悲观剪枝。
整理如下:
悲观剪枝参考了一本统计书籍:
《Statistical Methods》(7th edition) Snedecor,G.W. and Cochran,W.G.(1980)
论文相关部分如下:



整理成伪代码如下:
K:当前子树的总数据条数
J:当前子树分错的数据条数
E:剪枝后的分错的数据条数
∑
J
\sum J
∑J:一个叶子节点分类出错的数据条数
L ( S ) L(S) L(S):被判断是否需要剪枝的子树的所有叶子节点的数量
∑
J
+
1
2
L
(
S
)
\sum J+\frac{1}{2}L(S)
∑J+21L(S):悲观地猜测,如果不剪枝,那么该子树的所有叶子节点将会估计错误的数据条数
top to down方式剪枝
分错的数量的分布视为二项分布
剪枝后的分错的数据条数=E+
1
2
\frac{1}{2}
21
---------------
上面所有需要+
1
2
\frac{1}{2}
21的原因来自前面提到的参考文献的:
《Statistical Methods》(7th edition) Snedecor,G.W. and Cochran,W.G.(1980)的pp.117ff(这个到底是第几页的意思我也不知道,反正这本书似乎网上找不到pdf了)
---------------
如果剪枝后的
E
+
1
2
E+\frac{1}{2}
E+21<
∑
J
+
1
2
L
(
S
)
\sum J+\frac{1}{2}L(S)
∑J+21L(S)+
o
n
e
s
t
a
n
d
a
r
d
e
r
r
o
r
o
f
∑
J
+
1
2
L
(
S
)
one \ standard \ error \ of \ {\sum J+\frac{1}{2}L(S)}
one standard error of ∑J+21L(S)
就把该子树用该字数中出现类别频率最高的叶子节点替换。
论文中的举例是:

把上面这棵决策树的黄色圆圈部分的子树替换为一个叶子。
判断过程如下:
1.由于该子树中只有一个叶子是非negative,其余都是negative,假如剪枝,那么得到的判据是:
E+
1
2
\frac{1}{2}
21=1.5
2.假如不剪枝,那么判据是:
∑
J
+
1
2
L
(
S
)
\sum J+\frac{1}{2}L(S)
∑J+21L(S)+
o
n
e
s
t
a
n
d
a
r
d
e
r
r
o
r
o
f
∑
J
+
1
2
L
(
S
)
one \ standard \ error \ of {\sum J+\frac{1}{2}L(S)}
one standard error of∑J+21L(S)
由于
∑
J
\sum J
∑J=0
且剪枝前的叶子数是4个,
所以该判据的结果是2+
2
\sqrt{2}
2
所以有1.5<2+
2
\sqrt{2}
2
所以剪去该分支。
PEP剪枝后的结果如下:

我们前面提到的是PEP的剪枝,这里的截图写的是CCP的剪枝。文中提到
所以该篇文章中,PEP和CCP的剪枝效果是一样的,都是Figure2
另外注意:这篇论文的
剪枝前数据有2238条
剪枝后数据有2241条
原有数据集是2541条
具体为什么会有这个差别,作者没有明说,这个是由于unKnown(含缺失值)数据的处理方式没有详细阐述。
-----------------------
第二部分
论文是意大利人写的:
《A Comparative Analysis of Methods for Pruning Decision Trees》1997年,两种算法各个组成部分的对应关系如下:
| 1986年版本-Quinlan | 1997年版本- Floriana Esposito |
|---|---|
| E+ 1 2 \frac{1}{2} 21 | e’(t)=e(t) + 1 2 \frac{1}{2} 21 |
| ∑ J + 1 2 L ( S ) \sum J+\frac{1}{2}L(S) ∑J+21L(S) |  |
| one standard error of ∑ J + 1 2 L ( S ) {\sum J+\frac{1}{2}L(S)} ∑J+21L(S) | 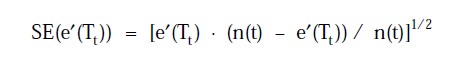 |
| E+ 1 2 < ∑ J + 1 2 L ( S ) + s t a n d a r d e r r o r o f ( ∑ J + 1 2 L ( S ) ) \frac{1}{2} <\sum J+\frac{1}{2}L(S)+standard \ error \ of{(\sum J+\frac{1}{2}L(S))} 21<∑J+21L(S)+standard error of(∑J+21L(S)) |  |
注意,这里第三栏的标准差是同一个意思
Quinlan是对分类错的数据条数先修正,然后求标准差,
这里
1
2
L
(
S
)
的
标
准
差
是
0
,
所
以
其
实
这
里
是
是
在
计
算
∑
J
的
标
准
差
\frac{1}{2}L(S)的标准差是0,所以其实这里是是在计算\sum{J}的标准差
21L(S)的标准差是0,所以其实这里是是在计算∑J的标准差
Floriana Esposito是直接把error的分布当做二项分布处理,使用了
V
a
r
=
n
p
q
=
分
错
的
数
量
⋅
(
总
数
-
分
错
的
数
量
)
总
数
Var=\sqrt{npq}=\sqrt{\frac{分错的数量·(总数-分错的数量)}{总数}}
Var=npq=总数分错的数量⋅(总数-分错的数量)
这两个版本的PEP剪枝的区别总共有1处:
Quinlan版本的PEP判据是<,
Floriana Esposito版本的PEP判据是≤
《Simplifying Decision Trees》-1986的part 2.3 Pessimistic Pruning 中
,
计算one standard error of
∑
J
+
L
(
S
)
2
\sum{J}+\frac{L(S)}{2}
∑J+2L(S)时,
L
(
S
)
2
\frac{L(S)}{2}
2L(S)的方差肯定是0,因为L(S)是叶子数量。
所以:
standard error of
∑
J
+
L
(
S
)
2
\sum{J}+\frac{L(S)}{2}
∑J+2L(S)
=standard error of
∑
J
\sum{J}
∑J
=
n
′
(
T
t
)
⋅
(
N
(
t
)
−
n
′
(
T
t
)
)
N
(
t
)
{\sqrt{\frac{n'(T_t)·(N(t)-n'(T_t))}{N(t)}}}
N(t)n′(Tt)⋅(N(t)−n′(Tt))
=
n
′
(
T
t
)
(
1
−
n
′
(
T
t
)
N
(
t
)
)
{\sqrt{n'(T_t)(1-\frac{n'(T_t)}{N(t)})}}
n′(Tt)(1−N(t)n′(Tt))
≈
n
′
(
T
t
)
{\sqrt{n'(T_t)}}
n′(Tt)
=
2
\sqrt{2}
2
=1.41
这个PEP的原理到底啥意思呢?
意思就是当前错误数被当做是一个变量的平均,当这个错误数量+这个变量的标准差时,就可以接近这个 变量的最大值。
把这个接近变量的最大值当做悲观错误数。
那么,作者没有解释的是,为什么“当前错误数”被假设为“一个变量的平均呢”,这明明不是变量啊~!
这是因为:一套数据集我们都是reshuffle后随机取其中的70~80%作为训练集的,由此导致的一个结果就是,到达某个子树的数据集被错分的数量是不定的,所以把当前子树的被错分数据的数量“视为”(assumption)一个变量来处理。
再作一个总结:
Quinlan发布的C4.5-Release8中使用的剪枝算法是EBP(Error Based Pruning)
http://www.rulequest.com/Personal/c4.5r8.tar.gz
weka中的J48使用的两种剪枝算法是EBP和REP
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








