递归思想

递归（recursion）是一个过程或函数在其定义或说明中又直接或间接调用自身的一种方法。

递归算法设计，就是把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题，在逐步求解小问题后，再返回（回溯）得到大问题的解。递归算法设计的关键在于找出递归关系（方程）和递归终止（边界）条件。递归关系就是使问题向边界条件转化的规则。递归关系必须能使问题越来越简单，规模越来越小。递归边界条件就是所描述问题最简单的、可解的情况，它本身不再使用递归的定义。

用递归算法解题，通常有3个步骤：

• 分析问题、寻找递归关系：找出大规模问题与小规模问题的关系，这样通过递归使问题的规模逐渐变小。
• 设置边界、控制递归：找出停止条件，即算法可解的最小规模问题。
• 设计函数、确定参数：和其他算法模块一样设计函数体中的操作及相关参数。

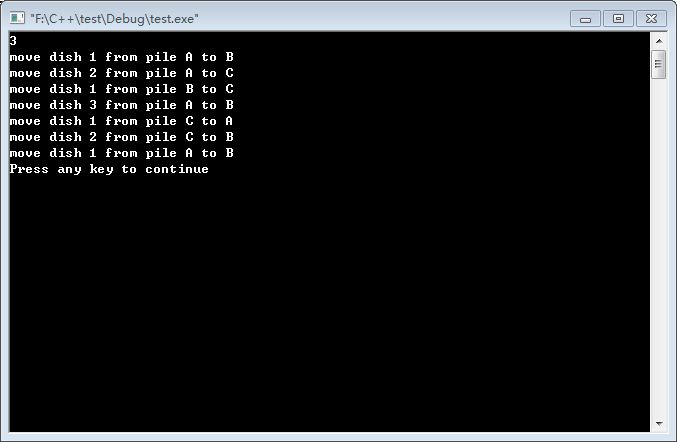
1、汉诺塔问题：古代有一个梵塔，塔内有3个基座A，B，C，开始时A基座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个老和尚想把这64个盘子从A座移到B座，但每次只允许移动一个盘子，且在移动过程中，3个基座上的盘子都始终保持大盘在下，小盘在上。移动过程中可以利用C基座做辅助。请编程打印出移动过程。

解析：

把n个盘子抽象地看作“两个盘子”，上面“一个”由1 - n-1号组成，下面一个就是n号盘子。移动过程如下：

• 先把上面“一个”盘子以A基座为起点借助B基座移到C基座。
• 把下面一个盘子从A基座移到B基座。
• 再把C基座上的“一个”盘子借助A基座移到B基座。

把n阶汉诺塔问题记作hanoi(n, a, b, c)，注意这里a，b，c并不总代表A，B，C3个基座，其意义为：第一个参数a代表每一次移动的起始基座，第二个参数b代表每一次移动的终点基座，第三个参数c代表每一次移动的辅助基座。由上述约定，n阶的汉诺塔问题记作hanoi(n, a, b, c)，a，b，c初值为“A”，“B”，“C”，以后的操作等价于以下3步：

• hanoi(n-1, a, c, b)；
• 把下面“一个”盘子从A基座移到B基座；
• hanoi(n-1, c, b, a)；

至此找出了大规模问题与小规模问题的递归关系。操作过程如下：

• 将A杆上面的n-1个盘子，借助B杆，移到C杆上。
• 将A杆上剩余的一个n号盘子移到B杆上。
• 将C杆上的n-1个盘子，借助A杆，移到B杆上。

算法实现：

#include<stdio.h>

void hanoi(int n, char a, char b, char c)
{
	if(n >0) {
		hanoi(n-1, a, c, b);
		printf("move dish %d from pile %c to %c", n, a, b);
		printf("\n");
		hanoi(n-1, c, b, a);
	}
}

void main() 
{
	int n;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
}

结果输出：

说明：

用0阶的汉诺塔问题当作停止条件即可。

总结：

递归算法执行中有递归调用的过程和回溯的过程（当然二者是不可分的），递归法就是通过递归调用把问题从大规模归结到小规模，当最小规模得到解决后又把小规模的结果回溯，从而推出大规模的解。

2、整数的分划问题

对于一个正整数n的分划，就是把n表示成一系列正整数之和的表达式。注意，分划与顺序无关，例如6 = 5 + 1和6 = 1 + 5被认为是同一种分划。另外，这个整数n本身也算是一种分划。

例如，对于正整数n = 6，它可以分划为：

6

5 + 1

4 + 2                    4 + 1 + 1

3 + 3                    3 + 2 + 1                    3 + 1 + 1 + 1

2 + 2 + 2              2 + 2 + 1 + 1              2 + 1 + 1 + 1 + 1

1 + 1 + 1 + 1 + 1 + 1

解析：

从上面n = 6的实际例子可以看出，很难找到大规模问题P(n)与小规模问题P(n-d)(d = 1, 2, 3, ...)的关系。根据n = 6的实例发现“第一行及以后的数据不超过6，第二行及以后的数据不超过5，......，第六行的数据不超过1”。因此，定义一个函数Q(n, m)，表示整数n的“任何加数都不超过m”的分划的数目，n的所有分划数目P(n)就应该表示为Q(n, n)。

一般地Q(n, m)有以下递归关系：

(1)Q(n, n) = Q(n, n-1)

等式右边的“1”表示n只包含一个被加数等于n本身的分划；则其余的分划表示n的所有其他分划，即最大加数m <= n-1的划分。

(2)Q(n, m) = Q(n, m-1) + Q(n-m, m)(m < n) 

等式右边的第一部分表示被加数中不包含m的分划的数目；第二部分表示被加数中包含（注意不是小于）m的分划的数目，因为如果确定了一个分划的被加数中包含m，则剩下的部分就是对n-m进行不超过m的划分。

到此找到了大规模问题与小规模问题的递归关系，下面是递归的停止条件：

(1)Q(n, 1) = 1，表示当最大的被加数是1时，该整数n只有一种分划，即n个1相加；

(2)Q(1, m) = 1，表示整数n = 1只有一个分划，不管最大被加数的上限m是多大。

算法实现：

#include<stdio.h>

int Divinteger(int n, int m)
{
    if((n<1) || (m<1)) 
		return 0;
    else if(n==1 || m==1) return 1;
    else if(n < m) 
		return Divinteger(n, n);
    else if(n == m) 
		return (Divinteger(n, m-1) + 1);
    else 
		return (Divinteger(n, m-1) + Divinteger(n-m, m));
}

int main()
{
	int n, count;
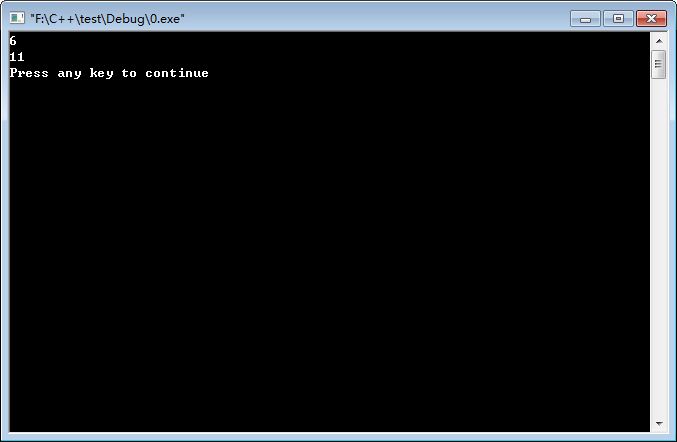
	scanf("%d", &n);
	count = Divinteger(n, n);
    printf("%d\n", count);
    return 0;
}

结果输出：

说明：

考虑算法的稳健性，如果n < m，则Q(n, m)是无意义的，因为n的分划不可能包含大于n的被加数m，此时令Q(n, m) = Q(n, n)；同样当n < 1或m < 1时，Q(n, m)也是无意义的。

分类讨论思想：

(1)m = 1或n = 1；(2)m > n；(3)m = n；(4)m < n。

3、递归与循环的比较

重复处理大量数据的步骤可以抽象成“循环”或“递归”的模式。循环模式算法设计的重点是循环不变式的构造过程，而递归模式算法设计的重点是递归不变式的构造过程。

每个迭代算法原则上总可以转换成与它等价的递归算法；反之不然，即并不是每个递归算法都可以转换成与它等价的循环结构算法。

说明：

递归在很多算法策略中得以运用，如分治策略、动态规划、图的搜索等算法策略。