Logit和Probit模型的中介效应分析

arlionn

于 2024-10-30 11:11:56 发布

阅读量340

点赞数

文章标签：连享会 Stata Logit Probit 中介效应分析

原文链接：https://www.lianxh.cn/details/1404.html

版权

温馨提示：若页面不能正常显示数学公式和代码，请阅读原文获得更好的阅读体验。

阅读全文：Logit和Probit模型的中介效应分析

作者：贾寰宇 (厦门大学)
邮箱：jhy13261692355@163.com

编者按：本文主要整理自下文，特此致谢！
Source：Breen R, Karlson K B, Holm A. Total, direct, and indirect effects in logit and probit models[J]. Sociological Methods & Research, 2013, 42(2): 164-191. -Link- -PDF- -Google-

Title：Logit和Probit模型的中介效应分析
Keywords：Logit 模型，Probit 模型，直接效应，间接效应

1. 问题背景

在某些研究中，我们可能需要关注 Logit 和 Probit 模型中的中介效应分析。举例来说，当我们探究不同种族间收入差异的根源时，不均匀的教育资源分配可能是一个关键因素。为了评估中介效应，研究者通常会设定一组包含不同中介变量的模型，进而比较同一核心解释变量在这些模型中的回归系数。

在线性模型中，这些系数的差异衡量了预测变量 xx 对结果变量 yy 的影响通过中介变量而产生的关联程度。这是基于 路径分析 的原理。该原理将变量 xx 对变量 yy 的效应分解为两部分，一部分由变量 zz 介导，另一部分未被 zz 介导。以 zz 为中介的部分称为间接效应，而未以 zz 为中介的部分称为直接效应。

间接效应和直接效应的总和称为总效应，它等于当不包含中介变量时，xx 对 yy 的效应。具体如下所示：

y∗=βyxx+e(1)y∗=βyxx+e(1)

y∗=βyx⋅zx+βyz⋅xz+v(2)y∗=βyx⋅zx+βyz⋅xz+v(2)

z=θzxx+w(3)z=θzxx+w(3)

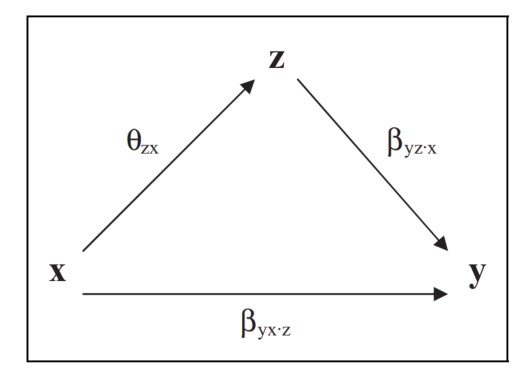
直接效应：βyx⋅zβyx⋅z
间接效应：θzx×βyz⋅xθzx×βyz⋅x
总效应：βyx=βyx⋅z+θzx×βyz⋅xβyx=βyx⋅z+θzx×βyz⋅x

然而，在 Logit 和 Probit 等非线性二元概率模型中，总效应无法像线性模型那样分解为直接效应和间接效应 (Fienberg，1977；Karlson 等，2012；MacKinnon 和 Dwyer，1993；Winship 和 Mare 1983)。这是因为在非线性二元概率模型中，误差方差可能在不同模型中有所不同，回归系数和误差方差不能分别识别。

相反，模型返回的系数估计值等于真实回归系数与一个缩放参数的比值，该缩放参数是误差标准差的函数 (Amemiya，1975；Winship 和 Mare，1983)。