LR(Logistic Regression) 逻辑回归模型 进行二分类或多分类 及梯度下降学习参数

逻辑回归(Logistic Regression, LR)是传统机器学习中的一种分类模型，由于算法的简单和高效，在实际中应用非常广泛。它的起源非常复杂，可以看参考引用1。具体应用实践可以看这里。

问题背景

对于二元分类问题，给定一个输入特征向量$X$(例如输入一张图片，通过算法识别它是否是一只猫的图片)，算法能够输出预测，称之为$\hat y$，也就是对实际值$y$的估计。或者说，$\hat y$表示$y$等于1的一种可能性或是置信度(前提条件是给定了输入特征$X$)。

如果代入带线性回归的模型中$\hat y=w^Tx$：

假设输入$X$为肿瘤大小，上图表示$y$值大于0.5时算法预测为恶性肿瘤，小于0.5时预测为良性肿瘤。看上去好像没有什么问题，但是在$y$值大于1或者小于0的地方不能很好地表示分类的置信度。再者看下图：

如果新加入了一个样本点(最右)，那么预测很可能就会如上图不是很准确了，恶性肿瘤的前几个样本点会被线性回归模型判定为良性肿瘤。因此我们引入sigmoid函数：

LR模型

Sigmoid函数

$$g(x) = \frac{1}{1 + e ^ {-x}}$$

从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在0点取值为0.5，在远离0的地方函数的值会很快接近0或是1。这个性质使我们能够以概率的方式来解释分类的结果。

所以对应条件概率分布(二分类)$P(Y|X)$为

$$P(y=1|x;w) = g(w^T x) = \frac{1}{1 + e ^ {-w^T * x}} \\\\P(y=0|x;w) = g(w^T x) = \frac{e ^ {-w^T * x}}{1 + e ^ {-w^T * x}}$$

参数求解

那么我们该如何求救里面的参数$w$呢？常用的方法有梯度下降法,牛顿法和BFGS拟牛顿法。

梯度下降法

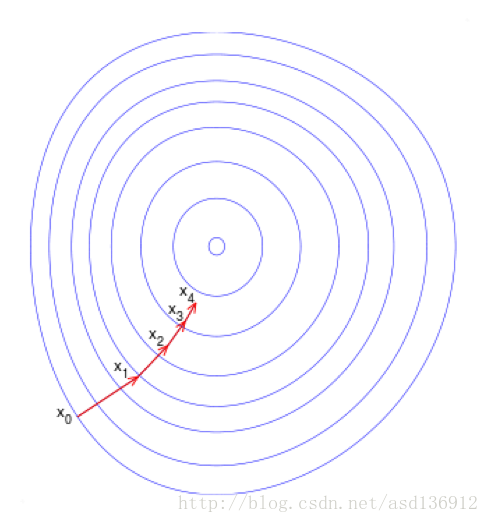
梯度下降(Gradient Descent)又叫作最速梯度下降，是一种迭代求解的方法，通过在每一步选取使目标函数变化最快的一个方向调整参数的值来逼近最优值。基本步骤如下：

1. 选择下降方向（梯度方向，$∇J(θ)$）
   • 选择步长，更新参数$θ_i=θ_{i−1}−α_i∇J(θ_{i−1})$
   • 重复以上两步直到满足终止条件
     
     我们首先定义一下损失函数Loss Function，如果我们使用常用的平方损失函数：
     $$L(\hat y,y)=\frac{1}{2}(\hat y-y)^2$$
     得到的函数图像如下左图，非凸函数有许多局部最小值，将会影响梯度下降寻找全局最小值。
     
     所以我们定义Lost Function为
     $$L(\hat y,y)=-(ylog\hat y+(1-y)log(1-\hat y))$$
     Cost Function $J$ (衡量算法在全部样本上的表现) 为：
     $$J=\frac{1}{m}\sum^m_{i=1}(\hat y^{(i)},y^{(i)})=\frac{1}{m}\sum^m_{i=1}(-y^{(i)}log\hat y^{(i)}-(1-y^{(i)})log(1-\hat y^{(i)}))$$
     其中上标i为第i个样本
     $$\frac{\partial{J}}{\partial{w}} = -\frac{1}{n}\sum_i (y^{(i)} - \hat y^{(i)})x^{(i)}$$
     更新weight
     $$w_j\leftarrow w_j+\alpha\sum^N_{i=1}[y_i-\sigma(w^Tx_i)]x_{i,j}$$
     Python的伪代码如下(对n个样本实现向量化)：

   • Z  = np.dot(w.T,x) + b
     A = sigmoid(Z)
     dZ = A - Y
     dw = 1/m * X * dZ.T
     db = 1/m * np.sum(dZ)
     w = w - a*dw
     b = b - a*db

     正则化

     当模型的参数过多时，很容易遇到过拟合的问题。这时就需要有一种方法来控制模型的复杂度，典型的做法在优化目标中加入正则项，通过惩罚过大的参数来防止过拟合：
     
     

     $$J(w) = -\frac{1}{N}\sum {y\log{g(w^T x)} + (1-y)\log{(1-g(w^T x))}} + \lambda \Vert w \Vert_p$$
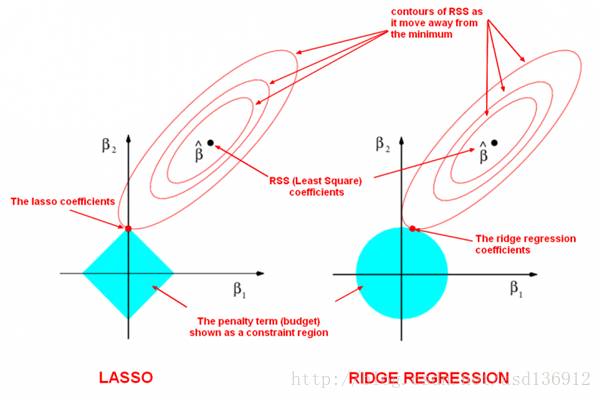
     其中q=1或2,即L1或是L2正则，详细介绍具体选择可以参考 Lasso正则
     
     如上图椭圆和蓝色的区域（惩罚函数）的切点就是目标函数的最优解，可以看到如果蓝色区域是圆，则很容易切到圆周的任意一点，但是很难切到坐标轴上，这样就得不出稀疏的借，冗余数据就会相对较多；但是如果蓝色区域是菱形或者多边形，则很容易切到坐标轴上，因此很容易产生稀疏的结果。这也说明了为什么1范式会是稀疏的。

     多分类

     延展到多分类问题(即softmax, 在NN上经常作为输出函数用到)，有以下条件概率分布与决策函数：
     

     $$P(y=i|x, w) = \frac{e^{w^T x}}{\sum_j^K{e^{w^T x}}} \\\\\hat y = \textrm{argmax}_i P(y=i|x,w)$$
     对应的损失函数为：
     $$J(w) = -\frac{1}{N} \sum_i^N \sum_j^K {1[y_i=j] \log{\frac{e^{w^T x}}{\sum {e^{w^T x}}}}}$$

     参考文献

     1. https://chenrudan.github.io/blog/2016/01/09/logisticregression.html
     2. https://tech.meituan.com/intro_to_logistic_regression.html
     3. 吴恩达，机器学习网课
     4. 周志华，机器学习
     5. 李航，统计学习方法