压缩感知与磁共振成像

01 压缩感知原理和建模

传统的数据采样和重构需要遵循Nyquist采样定律，即采样频率必须大于信号频率带宽的2倍，才能完整的重建信号。如果采样频率低于2倍的频率带宽，信号在频域频谱搬移后就会发生混叠，产生伪影。

压缩感知（Compressed Sensing）理论提出：如果一个信号是稀疏的，或者在其某个变换域是稀疏的，那么信号可以从远低于Nyquist采样定律的采样频率中重建出来，即稀疏或可压缩信号从其投影到某个子空间的少量值上通过非线性重建。

假设一个信号 $x\in R^{N\times 1}$，存在正交变换 $\Psi \in R^{N\times N}$，在此变换域中$x$的稀疏表示 $s\in R^{N\times 1}$是$K$稀疏的，那么可以通过一个观测矩阵 $\Phi \in R^{M\times N}$，产生一个观测向量 $y\in R^{M\times 1}$，满足$K<M\ll N$，$y$即采样值（已知）。压缩感知问题就是在已知测量值$y$和测量矩阵$\Phi$的基础上，求解欠定方程组$y=\Phi \Psi s$得到原信号$x$，$x=\Psi s$。

可以将该问题建模成一个优化问题，在数据保真项的约束下，通过控制$s$的稀疏程度（实际应用中更通常使用$l_1$范数），求解以下反问题，可以从少量的信号采样中，得到最终的信号重建结果：
$$\underset{s}{\min }||s|{|}_{l_0},s.t.\Phi \Psi s=y$$
想要通过CS理论重构出精确的原始信号，需要满足以下三个要求[2]：

①信号的稀疏性：待重建信号需要在某一个变换域（包括恒等变换）是稀疏的，即可压缩的；

②非相关性/等距约束性：非相关性要求欠采样造成的伪影和信号在稀疏表示下是不相关（noise-like）的，这样可以通过非线性算法从带有混叠伪影的信号中重构出原始信号。这一条件约束的是测量矩阵$\Phi$，要求观测矩阵满足有限等距性质（RIP），RIP的等价条件是观测矩阵和稀疏表示基不相关（incoherent）。独立同分布的高斯随机矩阵、随机部分傅里叶矩阵都可以作为普适的测量矩阵；

③非线性重构算法：从$M$维测量向量$y$重构长度为$N(M\ll N)$的原始信号$x$是一个NP-hard问题，无法直接求得最优解，只能通过高度非线性的最优化算法求得其次最优解。

02 压缩感知在MRI上的应用

MR图像的变换稀疏性和MR采集的编码性质是使CS在MRI中实现的两个关键特性。

磁共振成像由于其K空间采样和磁共振图像的稀疏性，以及临床上快速成像的要求，非常适合压缩感知的应用。

大部分的磁共振图像是稀疏的（如血管造影）或者在特定的变换域如小波变换、有限差分变换下具有很好的稀疏表示。自然的满足了压缩感知的第一条要求， 稀疏性是利用压缩感知重建磁共振图像的基础 。

MRI在K空间即频率空间采集数据，再通过反傅里叶变换得到空间域坐标值，傅里叶变换矩阵作为观测矩阵可以增加非相干性，前一小节中提到随机部分傅里叶矩阵满足等距约束性，可以作为观测矩阵产生不相干伪影。然而囿于磁共振采集硬件和人体生理上的限制，采样轨迹必须是相对平滑的直线或曲线，完全的随机采样是无法实现的。如何设计合理的欠采样方案，使得重建出的图像在稀疏域上的混叠伪影尽可能少，是快速磁共振成像的一个关键问题。

除此之外，MR图像在k空间中的能量分布并不是均匀的，MR I中的大部分能量集中在靠近 k-space 的中心，并向四周衰减，因此欠采样方案的设计应该具有可变密度，在k空间中心附近采样更加密集，同时采样轨迹要尽可能的不规则（随机）以满足观测矩阵的不相干性要求，满足以上条件的欠采样越快越好。

此时压缩感知模型中的观测矩阵$\Phi$对应于部分傅里叶变换矩阵$F_u=PF$，其中$P$是采样矩阵（对应于我们常说的mask），由0和1组成，$F$是傅里叶变换矩阵，图中给出了一些欠采样方案例子。

满足稀疏性和非相干性要求的MRI重建过程可以建模成以下优化问题：
$$\underset{x}{\min }||\Psi x|{|}_1,s.t.||Ax-y|{|}_2<ϵ$$
其中$A$为感知（观测）矩阵，单通道数据情况下$A=PF$，多通道数据情况下$A=SPF$，$S$是线圈敏感度矩阵，用来合并和恢复多通道数据。

有时还会加入全变分（TV）算子作为一个惩罚项，TV被定义为图像中绝对变化的总和，目标函数变为：
$$\underset{x}{\min }||\Psi x|{|}_1+\alpha TV(x),s.t.||Ax-y|{|}_2<ϵ$$
其中$\alpha$是参数，用于权衡稀疏性约束和TV约束。

03 非线性重建算法

上述优化问题可以转化成拉格朗日形式：
$$\underset{x}{\mathrm{argmin}}\lambda ||\Psi x|{|}_1+||Ax-y|{|}_2^2$$
或者加入TV算子：
$$\underset{x}{\mathrm{argmin}}\lambda ||\Psi x|{|}_1+\alpha TV(x)+||Ax-y|{|}_2^2$$
其中$\alpha$和$\lambda$都是参数

解决该优化问题的主要难度来自于$l_1$范数和变分算子等正则项的不可微性，导致无法直接通过线性最小二乘算法求解，转而寻求更多的非线性迭代算法。下面简单介绍几种常见的非线性算法：

①非线性共轭梯度法

Lustig等人[1]将小波变换作为稀疏变换应用于CS-MRI，建立如下图像重建模型，并采用非线性共轭梯度下降算法和回溯线搜索进行求解：
$$x=\underset{m}{\mathrm{argmin}}\frac{1}{2}||F_{u}m-y|{|}_2^2+\lambda ||\Psi m|{|}_1$$
非线性共轭梯度法将线性共轭梯度（CG）法扩展到非线性求解问题，用CG的方式计算优化方向，然后用回溯线搜索算法计算一个可接受的步长，用梯度$\Delta f_k$替代残差$g_k$

对于非线性共轭梯度法的关键在于如何去计算梯度$\Delta f(m)$，由于$l_1$范数是绝对值的和，并不是一个光滑可微的函数（这也是求解该优化问题的难点），Lustig等人用一个平滑函数$x\approx\sqrt{x*x+\mu } $来近似绝对值函数，这样就可以求得拉格朗日函数$f(m)$的近似梯度：
$$\Delta f(m)\approx F_u\ast (F_{u}m-y)+\lambda \Psi \ast W^{-1}\Psi m$$
其中$W$是对角矩阵，对角元素$w_i=\sqrt{(\Psi m{)}_i\ast (\Psi m{)}_i+\mu }$

算法流程：

②迭代软阈值算法（Iterative Shrinkage Thresholding Algorithm，ISTA）

在凸优化问题中，对于可微分的目标函数，可以通过梯度下降法（gradient descent）迭代求得最优解；对于不可微分的目标函数，引入次梯度（subgradient）也可以求解，但速度比较缓慢。为此，针对一些整体不可微分，但却可以分解的目标函数，引入近端梯度法(Proximal Gradient Descent)，用来解决包含不可导项的优化问题。

对于一个目标函数可以分解成如下形式的：
m i n   f ( x ) = m i n { g ( x ) + h ( x ) } min\ f(x)=min\{g(x)+h(x)\} min f(x)=min{g(x)+h(x)}
其中，$g(x)$是凸函数且可以微分，$h(x)$也是凸函数但可能不可微分，仍然可以用平滑部分$g$的二次近似来定义向最优解下降的一步。

定义近端函数$prox$为$pro{x}_{h,t}(x)=\underset{z}{\mathrm{argmin}}\frac{1}{2t}||x-z|{|}_2^2+h(z)$
$$\begin{gathered} x^{\ast }=\underset{z}{\mathrm{argmin}}g(z)+h(z)\approx \underset{z}{\mathrm{argmin}}g(x)+▽g(x{)}^T(z-x)+\frac{1}{2t}||z-x|{|}_2^2+h(z) \\ {x}^{\ast }=\underset{z}{\mathrm{argmin}}[\frac{1}{2t}||z-(x-t▽g(x))|{|}_2^2+h(z)]=pro{x}_{h,t}(x-t▽g(x)) \end{gathered}$$

迭代软阈值算子为近端算子的一种形式，当$h(x)$为$l_1$范数的形式时：

$$pro{x}_t(x)=\underset{z}{\mathrm{argmin}}\frac{1}{2t}||x-z|{|}_2^2+||z|{|}_1=\underset{z}{\mathrm{argmin}}||x-z|{|}_2^2+2t||z|{|}_1=S_t(x)$$

$S_t(x)$为软阈值算子，

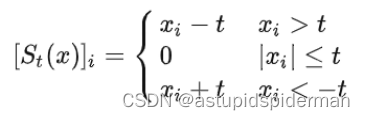
Ricardo Otazo等人[4]用L+S分解模型求解动态磁共振成像问题时用到了迭代软阈值方法，L+S模型为：
$$\underset{L,S}{\min }\frac{1}{2}||E(L+S)-d|{|}_2^2+{\lambda }_L||L|{|}_{\ast }+{\lambda }_S||TS|{|}_1$$
${\lambda }_L$和${\lambda }_S$是参数，用来权衡数据一致性与核范数和$l_1$范数之间的关系。

在迭代求解L和S时用到了软阈值算子（也称为收缩算子）${\Lambda }_{\lambda }(x)=\frac{x}{|x|}max(|x|-\lambda ,0)$，每一步迭代更新L和S，最后利用得到的L和S计算矩阵M

算法流程：

③增广拉格朗日和ADMM

由于$l_1$范数不可微，可以采用变量分离法（Variable Splitting Method），如增广拉格朗日算法等，通过引入辅助变量，将上面带TV算子约束项的优化问题替换为一个包含辅助变量的等式约束最小化问题，Junfeng Yang等人[5]引入辅助变量$w=[w_1,...,w_N],w_i\in R^2$和$z\in R^N$，问题建模为：
$$\begin{gathered} \underset{w,z,u}{\min }\sum _i||w_i||+\tau ||z|{|}_1+\frac{1}{2}\mu ||F_{p}u-f_p|{|}_2^2, \\ s.t.w_i=D_{i}u,\forall i;z={\Psi }^{T}u \end{gathered}$$
其中$u$表示待重建图像，$f_p$为到的采集信号，$D_{i}u$被定义为全变分（TV）的离散化。

增广拉格朗日方法通过增加罚项，将不光滑不可微的项转变为光滑的表示，

引入函数${\varphi }_1(s,t,v)$和${\varphi }_2(s,t,\overrightarrow{v})$分别对应$||z|{|}_1$项和$||w_i||$项，
$$\begin{gathered} {\varphi }_1(s,t,v)=\tau |s|-v(s-t)+({\beta }_1/2)|s-t{|}^2 \\ {\varphi }_2(s,t,\overrightarrow{v})=\tau ||s||-{\overrightarrow{v}}^T(s-t)+({\beta }_2/2)||s-t|{|}^2 \end{gathered}$$
这样不可微的项就变成了一个二次凹函数，上述约束问题对应的增广拉格朗日函数为：
$$L_A(w,z,u,{\lambda }_1,{\lambda }_2)=\sum _i{\varphi }_2(w_i,D_{i}u,({\lambda }_2{)}_i)+\sum _i{\varphi }_1(z_i,{\Psi }_i^{T}u,({\lambda }_1{)}_i)+\frac{1}{2}\mu ||F_{p}u-f_p|{|}_2^2$$
增广拉格朗日函数的求解可以通过下面的迭代流程：

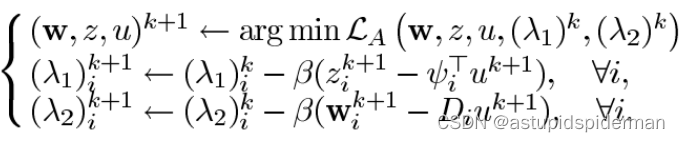
虽然解决了不可微的问题，但迭代求解第一项仍然是很麻烦的，为了保证ALM的收敛性，在乘子迭代更新之前，需要将每个最小化子问题求解到一定的高精度，并且第一项要达到$w,z,u$的联合最小化。此时可以利用交替乘子迭代法（ADMM），利用$L_A$中变量的可分离结构，每次迭代时仅执行一次交替最小化，然后立即更新乘子，大大降低迭代成本。

算法流程：

④原始-对偶法

通过构建原始变量$x$的对偶变量$z$，在原始变量$x$和对偶变量$z$交替迭代更新[6]

参考文献

【1】Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007

【2】M. Lustig, D. L. Donoho, J. M. Santos and J. M. Pauly, “Compressed Sensing MRI,” in IEEE Signal Processing Magazine, March 2008.

【3】Saman Khoramian, An iterative thresholding algorithm for linear inverse problems with multi-constraints and its applications, Applied and Computational Harmonic Analysis, 2012

【4】Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015 Mar

【5】Yang, Junfeng et al. “A Fast Alternating Direction Method for TVL1-L2 Signal Reconstruction From Partial Fourier Data.” IEEE Journal of Selected Topics in Signal Processing 4 (2010): 288-297.

【6】Chambolle, A., Pock, T. A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. J Math Imaging Vis 40, 120–145 (2011).

【7】压缩感知原理简介_vivian_ll的博客-CSDN博客_压缩感知

【8】共轭梯度法（二）：非线性共轭梯度 - 知乎 (zhihu.com)

【9】[近端梯度下降与软阈值迭代：PGD and ISTA_三生断绝的博客-CSDN博客](https://blog.csdn.net/qq_42122496/article/details/106039034#:~:text=通常我们将 l1 范数对应的临近点算子称为软阈值，将 l0 范数对应的临近点算子称为硬阈值。 软阈值迭代算法,(ISTA%2C iterative soft-thresholding algorithm) ，即为用软阈值作为包含 l1 范数的目标函数的“梯度”，使用“梯度下降”来得到最优值的算法。)

【10】 优化算法-3|增广拉格朗日函数(ALM)及其优化方法-ADMM算法、AMA算法 - 知乎 (zhihu.com)