不正之处,欢迎指正。
1.概述
PCA:主成分分析,一种常用的数据分析方法,不管是在机器学习还是数据挖掘中都会用到。PCA主要通过求数据集的协方差矩阵最大的特征值对应的特征向量,由此找到数据方差最大的几个方向,对数据达到降维的效果,将一个n维的向量降低到d维,其中d<n。本文主要从方差最大化理论解释PCA的实现过程。
首先来看这样几个实际问题,比如那到一个汽车的样本,里面既有千米每小时度量的最大速度特征,也有英里每小时的速度特征,很明显这两者是存在冗余的,知道其中的一个就可以计算另外一个,在特征中并没有必要将二者同时包含在里面。再比如拿到一个数学系本科学生期末考试成绩单,里面有三列,一列是对数学的感兴趣程度,一列是复习时间,还有一列是考试成绩,很明显,考试成绩跟兴趣是相关的,跟复习所用的时间也是相似的,那么可不可以合并前面两列呢?
综合上面两个问题,可以发现,在样本中其实很多时候有些给定的特征是存在冗余的,我们希望在分类 时候所用到的特征都是和我们的标记是相关的,所以就可以用特征降维的方法减少特征数,较少噪声和冗余,减少过拟合的问题。接下来将先介绍PCA的数学基础,在理论基础上给出推导过程。
2.内积和基变换
两个向量的内积定义为向量的对应元素相乘之和,,
,则二者的内积表示为:
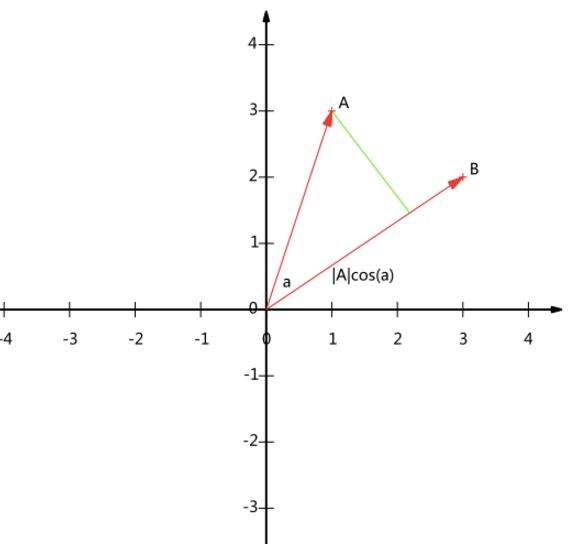
我们知道二者的内积也等价与: 如果向量a和b都是二维向量的话,用图像可以表示如下:
这个图像表示的意义就是向量a和向量b的内积等于向量a在向量b方向上的投影与向量b长度的乘积,如果将向量b的长度规定为1,那么二者的内积就是向量a在b方向的投影了。知道了这个之后我们介绍基的概念。
在二维的平面直角坐标系中,我们知道x轴和y轴分别是所有二维向量的一组正交基,所有的二维向量都可以用这两个向量的线性组合来表示,二维平面中的一组正交基规定为(1,0)和(0,1),比如说向量(3,2)在x轴和y轴上分别在投影的话,x轴上的距离就是3,y轴上的距离就是2,式子表示就是:,
,更一般的,向量
用这样的一组正交基表示为:
因此,要准确的描述一个向量,要选择一组基底,在选择基底的时候往往选择两两正交的单位正交基,这样就可以将坐标和向量对应,比如这里选择的(1,0)和(0,1),在三维空间中就是(1,0,0),(0,1,0),(0,0,1),以此类推。
用矩阵运算表示上面的过程,对于点(3,2)来说,上面的运算可以简化为:
3.期望方差与协方差矩阵
给定一个含有m个样本的集合:X={X1,…,Xm}
均值:
方差:
均值描述的是样本集合的平均值,方差描述的是样本集合中各个点到均值的距离的平均,也就是数据的离散程度。
如果数据的维数比较多的话,我们想知道某两个特征之间是否有关系,比如说统计学生的成绩,数学成绩和物理成绩
之间是否有关系,如果有是正相关呢还是负相关,协方差就是用来描述两个随机变量X,Y之间关系的统计量,协方差
定义如下:
协方差的结果为正的话,表明二者之间是正相关,为负的话表明二者之间是负相关。这里的X,Y两个一维的随机变量,
如果随机变量的个数很多呢,这时候就引入了协方差矩阵的概念:对于一个n维的数据,分别计算没两个维度之间的协方
差,就构成了一个协方差矩阵:
可见这是一个对称矩阵,对角线上的是方差。如果数据是三维的,则协方差矩阵如下:
4.最大方差理论
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。如前面的图,样本在横轴上的投影方差较大,在纵轴上的投影方差较小,那么认为纵轴上的投影是由噪声引起的。所以我们认为最好的k维特征是将n维的样本点转化之后,每一维上的样本方差都很大。
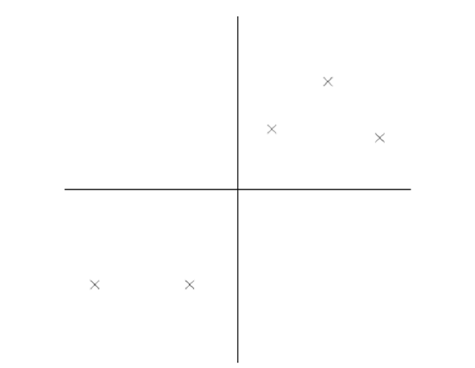
比如下图右5个样本点,所有的点已经做过预处理,均值为0,特征方差归一。
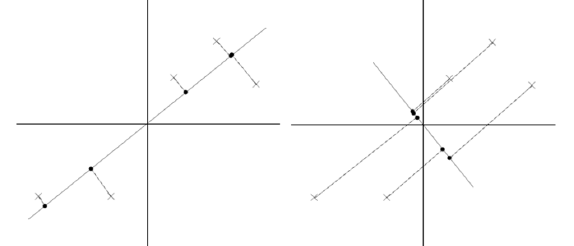
对与这样的一个二维平面上的点,我们现在想要把它投影到一个一维中去,也就是找到一条直线,将这些点全部投影到直线上去,达到降维的目的。下面是两条直线的比较.
很明显,左边那条直线的投影效果更好,数据的方差更大,越有利于分类。
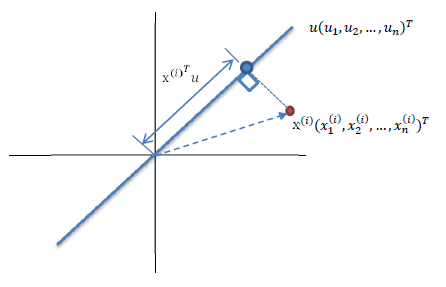
如图所示,红色的点表示的是样本点,蓝色的点表示的是样本点在向量u上的投影点,这里规定u是单位向量,则x在u上的投影可以表示为,假设现在有很多个样本点x,我们希望存在这样的一个u使得这些样本点投影到u上之后方差最大。由于样本点的每一维特征的均值都是0,所以投影到u上之后的样本点的均值也是0
计算方差:
很显然,中间括号的那一部分就是所有样本的协方差矩阵,唯一不同的地方就是协方差计算的时候是除m-1,这里是除m。好了,现在的目标就是要最小化这个式子,用表示协方差,用
表示优化目标,那么上述问题可以写成:
两边同时乘以u,u是单位向量,所以右边相乘的结果是1变成
也就是
观察可知,这就是协方差矩阵求解特征值和特征向量的形式,所以最好的投影直线就是对应的特征向量啊,第二好的就是对应的第二个特征向量。
对于多维特征空间,值需要对样本协方差矩阵进行特征值分解,得到前k个最大特征值对应的特征向量就是最佳的k维特征,而且这k维特征是正交的,得到前k个特征之后,样例可以通过以下的过程求解得到:
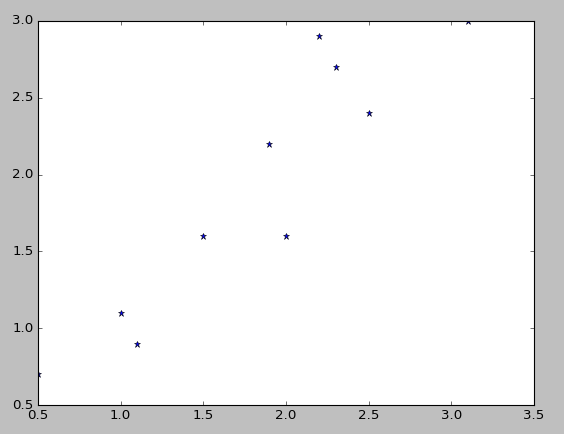
下面通过一个具体的实例实现PCA的过程,试验中的数据根据个人需要设计的。数据的二维分布如下所示:
现在通过PCA过程将数据由二维降到一维,只需要最大的特征值对应的特征向量即可。
<span style="font-size:14px;">import numpy as np
import matplotlib.pyplot as plt
data=np.array([[2.5,2.4],
[0.5,0.7],
[2.2,2.9],
[1.9,2.2],
[3.1,3.0],
[2.3,2.7],
[2.0,1.6],
[1.0,1.1],
[1.5,1.6],
[1.1,0.9]])
plt.plot(data[:,0],data[:,1],'*')
plt.show()
meandata=np.mean(data,axis=0) #计算每一列的平均值
data=data-meandata #均值归一化
covmat=np.cov(data.transpose()) #求协方差矩阵
eigVals,eigVectors=np.linalg.eig(covmat) #求解特征值和特征向量
pca_mat=eigVectors[:,-1] #选择第一个特征向量
pca_data=np.dot(data,pca_mat)
print(pca_data)</span>
5.参考文章
http://blog.csdn.net/ShiZhixin/article/details/51181379
http://lib.csdn.net/article/machinelearning/42816








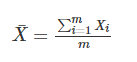
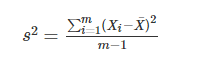
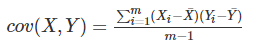

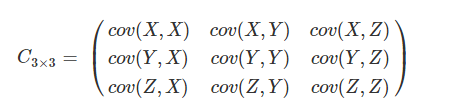
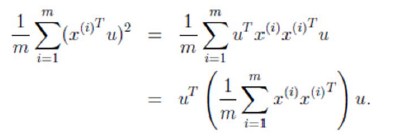
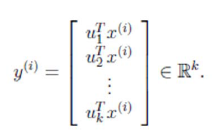














 5万+
5万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








