2.3 条件概率分布与随机变量的独立性
2.3.1 条件概率分布的概念
一个随机变量或向量 X X X的条件概率分布,就是在某种给定的条件之下, X X X的概率分布.
考虑之前提到的体重 X 1 X_1 X1与身高 X 2 X_2 X2的二维正态分布 N ( a , b , σ 2 1 , σ 2 2 , ρ ) N\left(a, b, \sigma_{2}^{1}, \sigma_{2}^{2}, \rho\right) N(a,b,σ21,σ22,ρ).根据之前的论述可以知道 X 1 X_1 X1, X 2 X_2 X2都有单独的概率分布,分别为 N ( a , σ 1 2 ) N\left(a, \sigma_{1}^{2}\right) N(a,σ12)和 N ( b , σ 2 2 ) N\left(b, \sigma_{2}^{2}\right) N(b,σ22). 现在如限制 1.7 ⩽ X 2 ⩽ 1.8 1.7 \leqslant X_{2} \leqslant 1.8 1.7⩽X2⩽1.8(米 ), 在这个条件下去求 X 1 X_{1} X1的 条件分布,这就意味着要从这一大群人中把其身高在 1.7 1.7 1.7米和 1.8 1.8 1.8米的那些人都挑出来,然后在挑出的人群中求其体重的分布. 容易想像, 这个分布与不设这个条件的分布 (无条件分布)会很不一样.体重取大值的概率会显著增加.
从这个例子也看出条件分布这个概念的重要性.
2.3.2 离散型随机变量的条件概率分布
这个比较简单,直接给例子.
多项分布的条件概率分布
设 ( X 1 , X 2 , ⋯ , X n ) \left(X_{1}, X_{2}, \cdots, X_{n}\right) (X1,X2,⋯,Xn)服从多项分布 M ( N ; p 1 , ⋯ , M\left(N ; p_{1}, \cdots,\right. M(N;p1,⋯,, p n p_{n} pn). 在给定 X 2 = k 2 X_{2}=k_{2} X2=k2的条件下, X 1 X_{1} X1的条件分布为 B ( N − k 2 , p 1 / ( 1 − p 2 ) ) B\left(N-k_{2}, p_{1} /\left(1-p_{2}\right)\right) B(N−k2,p1/(1−p2))
代数证明略去.这个公式的直观意义为在 X 2 = k 2 X_{2}=k_{2} X2=k2的条件下,剩下 n − 1 n-1 n−1个变量的联合分布就变为 n − k 2 n-k_2 n−k2个物品分成 n − 1 n-1 n−1堆,每个物品分到第 i i i堆的概率从 p i p_i pi变成 p i / ( 1 − p 2 ) p_i/(1-p_2) pi/(1−p2).那么 X 1 X_1 X1的条件分布就变为 M ( N − k 2 ; p 1 / ( 1 − p 2 ) , p 3 / ( 1 − p 2 ) , ⋯ , p n / ( 1 − p 2 ) ) M\left(N-k_2 ; p_{1}/(1-p_2), p_{3}/(1-p_2), \cdots,p_{n}/(1-p_2)\right) M(N−k2;p1/(1−p2),p3/(1−p2),⋯,pn/(1−p2))的边缘分布,即 B ( N − k 2 , p 1 / ( 1 − p 2 ) ) B\left(N-k_{2}, p_{1} /\left(1-p_{2}\right)\right) B(N−k2,p1/(1−p2))
2.3.3 连续型随机变量的条件分布
连续型随机变量的条件分布函数如下
- 当 a ≠ b a\neq b a=b时
f 1 ( x 1 ∣ a ⩽ X 2 ⩽ b ) = ∫ a b f ( x 1 , t 2 ) d t 2 / ∫ a b f 2 ( t 2 ) d t 2 f_{1}\left(x_{1} \mid a \leqslant X_{2} \leqslant b\right)=\int_{a}^{b} f\left(x_{1}, t_{2}\right) \mathrm{d} t_{2} / \int_{a}^{b} f_{2}\left(t_{2}\right) \mathrm{d} t_{2} f1(x1∣a⩽X2⩽b)=∫abf(x1,t2)dt2/∫abf2(t2)dt2
- 当 a = b = x 2 a=b=x_2 a=b=x2时
f ( x 1 ∣ x 2 ) = f 2 ( x 2 ) f 1 ( x 1 , x 2 ) f\left(x_{1}\mid x_{2}\right)=f_{2}\left(x_{2}\right) f_{1}\left(x_{1} , x_{2}\right) f(x1∣x2)=f2(x2)f1(x1,x2)
可以记为
f
(
x
1
,
x
2
)
=
f
2
(
x
2
)
f
1
(
x
1
∣
x
2
)
f\left(x_{1}, x_{2}\right)=f_{2}\left(x_{2}\right) f_{1}\left(x_{1} \mid x_{2}\right)
f(x1,x2)=f2(x2)f1(x1∣x2)
可以看出该公式对应于条件概率的公式
P
(
A
B
)
=
P
(
B
)
P
(
A
∣
B
)
P(A B)=P(B) P(A \mid B)
P(AB)=P(B)P(A∣B)
推广到任意多变量的场合
f ( x 1 , ⋯ , x n ) = g ( x 1 , ⋯ , x k ) h ( x k + 1 , ⋯ , x n ∣ x 1 , ⋯ , x k ) f\left(x_{1}, \cdots, x_{n}\right)=g\left(x_{1}, \cdots, x_{k}\right) h\left(x_{k+1}, \cdots, x_{n} \mid x_{1}, \cdots, x_{k}\right) f(x1,⋯,xn)=g(x1,⋯,xk)h(xk+1,⋯,xn∣x1,⋯,xk)
下面给出连续型随机变量的条件分布的例子
二维正态分布的条件分布
设
(
X
1
,
X
2
)
\left(X_{1}, X_{2}\right)
(X1,X2)服从二维正态分布
N
(
a
,
b
,
σ
1
2
,
σ
2
2
,
ρ
)
N\left(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)
N(a,b,σ12,σ22,ρ). 在给定
X
1
=
x
1
X_{1}=x_{1}
X1=x1的条件下,
X
2
X_{2}
X2的条件密度函数
f
2
(
x
2
∣
x
1
)
=
1
2
π
σ
2
1
−
ρ
2
⋅
exp
[
−
(
x
2
−
(
b
+
ρ
σ
2
σ
1
−
1
(
x
1
−
a
)
)
)
2
2
(
1
−
ρ
2
)
σ
2
2
]
\begin{aligned} f_{2}\left(x_{2} \mid x_{1}\right)=& \frac{1}{\sqrt{2 \pi} \sigma_{2} \sqrt{1-\rho^{2}}} \\ & \cdot \exp \left[-\frac{\left(x_{2}-\left(b+\rho \sigma_{2} \sigma_{1}^{-1}\left(x_{1}-a\right)\right)\right)^{2}}{2\left(1-\rho^{2}\right) \sigma_{2}^{2}}\right] \end{aligned}
f2(x2∣x1)=2πσ21−ρ21⋅exp[−2(1−ρ2)σ22(x2−(b+ρσ2σ1−1(x1−a)))2]
这正是正态分布
N
(
b
+
ρ
σ
2
σ
1
−
1
(
x
1
−
a
)
,
σ
2
2
(
1
−
ρ
2
)
)
N\left(b+\rho \sigma_{2} \sigma_{1}^{-1}\left(x_{1}-a\right), \sigma_{2}^{2}\left(1-\rho^{2}\right)\right)
N(b+ρσ2σ1−1(x1−a),σ22(1−ρ2))的概率密度函数.
由这里可以看出 ρ \rho ρ刻画了 X 1 , X 2 X_{1}, X_{2} X1,X2之间的相依关系.解释如下:
-
若 ρ > 0 \rho>0 ρ>0, 则随着 x 1 x_{1} x1的增加, X 2 X_{2} X2(在 X 1 = x 1 X_{1}=x_{1} X1=x1之下) 的条件分布的中心点 m ( x 1 ) m\left(x_{1}\right) m(x1)随 x 1 x_{1} x1的增加而增加. 可以看出: 这意味着当 x 1 x_{1} x1增加时, X 2 X_{2} X2取大值的可能性增加, 即 X 2 X_{2} X2有随着 X 1 X_{1} X1的增长而增长.若 ρ < 0 \rho<0 ρ<0则情况相反.若 ρ = 0 \rho=0 ρ=0则无关.这从中心点的角度刻画了 ρ \rho ρ对 X 1 X_1 X1, X 2 X_2 X2相依关系的刻画.
下图展示了 X 1 X1 X1分布为 N ( 25 , 64 ) N\left(25, 64\right) N(25,64)和 X 2 X_2 X2分布为 N ( 25 , 64 ) N\left(25, 64\right) N(25,64)时,不同 ρ \rho ρ下二维正态分布的概率密度.

下图展示了 r h o = 0.5 rho=0.5 rho=0.5时, X 1 = 15 , 25 , 35 X_1=15,25,35 X1=15,25,35下 X 2 X_2 X2的条件分布

-
若 ∣ ρ ∣ = 0 |\rho|=0 ∣ρ∣=0,则 σ = σ 2 \sigma=\sigma_2 σ=σ2, X 2 X_2 X2分布的集中程度不受 X 1 X_1 X1影响.现在考虑极端情况,假如 ∣ ρ ∣ = 1 |\rho|=1 ∣ρ∣=1,那么 σ = 0 \sigma=0 σ=0,由一维正态分布的性质可以知道 X 2 X_2 X2的取值全部集中于 m ( X 1 ) m(X_1) m(X1).也就是说, X 2 X_2 X2的取值由 X 1 X_1 X1完全决定.这从集中程度的角度刻画了 ρ \rho ρ对 X 1 X_1 X1, X 2 X_2 X2相依关系的刻画.
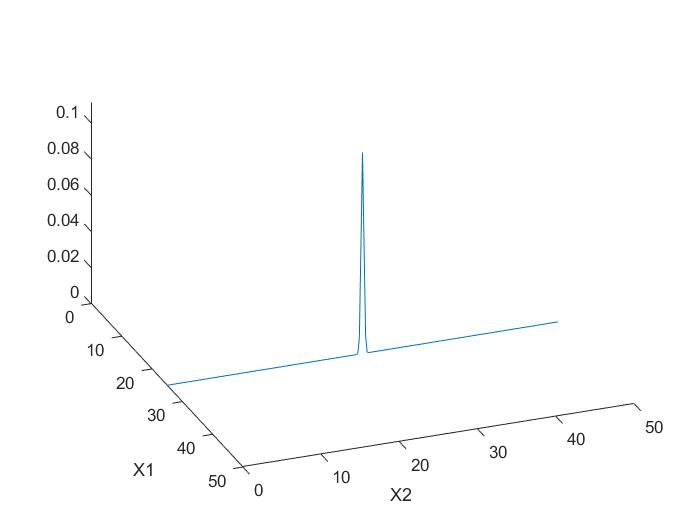
下图为 ρ = 0.999 \rho=0.999 ρ=0.999时 X 2 X_2 X2的条件分布
2.3.4 随机变量的独立性
定义
3.1
3.1
3.1设
n
n
n维随机向量
(
X
1
,
⋯
,
X
n
)
\left(X_{1}, \cdots, X_{n}\right)
(X1,⋯,Xn)的联合密度函数为
f
(
x
1
,
⋯
,
x
n
)
f\left(x_{1}, \cdots, x_{n}\right)
f(x1,⋯,xn), 而
X
i
X_{i}
Xi的(边缘)密度函数为
f
i
(
x
i
)
,
i
=
1
,
⋯
,
n
f_{i}\left(x_{i}\right), i=1, \cdots, n
fi(xi),i=1,⋯,n. 如 果
f
(
x
1
,
⋯
,
x
n
)
=
f
1
(
x
1
)
⋯
f
n
(
x
n
)
f\left(x_{1}, \cdots, x_{n}\right)=f_{1}\left(x_{1}\right) \cdots f_{n}\left(x_{n}\right)
f(x1,⋯,xn)=f1(x1)⋯fn(xn)
就称随机变量
X
1
,
⋯
,
X
n
X_{1}, \cdots, X_{n}
X1,⋯,Xn相互独立或简称独立
定义 3.2 设
X
1
,
⋯
,
X
n
X_{1}, \cdots, X_{n}
X1,⋯,Xn都是离散型随机变量. 若对任何常 数
a
1
,
⋯
,
a
n
a_{1}, \cdots, a_{n}
a1,⋯,an, 都有
P
(
X
1
=
a
1
,
⋯
,
X
n
=
a
n
)
=
P
(
X
1
=
a
1
)
⋯
P
(
X
n
=
a
n
)
P\left(X_{1}=a_{1}, \cdots, X_{n}=a_{n}\right)=P\left(X_{1}=a_{1}\right) \cdots P\left(X_{n}=a_{n}\right)
P(X1=a1,⋯,Xn=an)=P(X1=a1)⋯P(Xn=an)
则称
X
1
,
⋯
,
X
n
X_{1}, \cdots, X_{n}
X1,⋯,Xn相互独立
定理 3.1 3.1 3.1如果连续变量 X 1 , ⋯ , X n X_{1}, \cdots, X_{n} X1,⋯,Xn独立时, 则对任何 a i < a_{i}< ai< b i , i = 1 , ⋯ , n b_{i}, i=1, \cdots, n bi,i=1,⋯,n, 由 ( 3.14 ) (3.14) (3.14)定义的 n n n个事件 A 1 , ⋯ , A n A_{1}, \cdots, A_{n} A1,⋯,An也独立.
定理
3.2
3.2
3.2若连续型随机向量
(
X
1
,
⋯
,
X
n
)
\left(X_{1}, \cdots, X_{n}\right)
(X1,⋯,Xn)的概率密度函数
f
(
x
1
,
⋯
,
x
n
)
f\left(x_{1}, \cdots, x_{n}\right)
f(x1,⋯,xn)可表为
n
n
n个函数
g
1
,
⋯
,
g
n
g_{1}, \cdots, g_{n}
g1,⋯,gn之积, 其中
g
i
g_{i}
gi只依赖于
x
i
x_{i}
xi, 即
f
(
x
1
,
⋯
,
x
n
)
=
g
1
(
x
1
)
⋯
g
n
(
x
n
)
f\left(x_{1}, \cdots, x_{n}\right)=g_{1}\left(x_{1}\right) \cdots g_{n}\left(x_{n}\right)
f(x1,⋯,xn)=g1(x1)⋯gn(xn)
则
X
1
,
⋯
,
X
n
X_{1}, \cdots, X_{n}
X1,⋯,Xn相互独立,且
X
i
X_{i}
Xi的边缘密度函数
f
i
(
x
i
)
f_{i}\left(x_{i}\right)
fi(xi)与
g
i
(
x
i
)
g_{i}\left(x_{i}\right)
gi(xi)只 相差一个党数因子
定理
3.3
3.3
3.3若
X
1
,
⋯
,
X
n
X_{1}, \cdots, X_{n}
X1,⋯,Xn相互独立,而
Y
1
=
g
1
(
X
1
,
⋯
,
X
m
)
,
Y
2
=
g
2
(
X
m
+
1
,
⋯
,
X
n
)
Y_{1}=g_{1}\left(X_{1}, \cdots, X_{m}\right), Y_{2}=g_{2}\left(X_{m+1}, \cdots, X_{n}\right)
Y1=g1(X1,⋯,Xm),Y2=g2(Xm+1,⋯,Xn)
则
Y
1
Y_{1}
Y1和
Y
2
Y_{2}
Y2独立.





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








