二维正态分布参数 ρ \rho ρ的作用
我们知道,一个随机向量 X = X= X= ( X 1 , ⋯ , X n ) \left(X_{1}, \cdots, X_{n}\right) (X1,⋯,Xn)的分布 F F F足以决定其任一分量 X i X_{i} Xi的 ( \left(\right. (边缘)分布 F i F_{i} Fi, 但反过来不对: 即使知道了所有 X i X_{i} Xi的边缘分布 F i , i = 1 , ⋯ , n F_{i}, i=1, \cdots, n Fi,i=1,⋯,n, 也不足以决定 X X X的分布 F F F.而二维正态分布就是一个典型例子.
例如,考察边际分布为 N ( 25 , 16 ) N\left(25, 16\right) N(25,16)和 N ( 25 , 64 ) N\left(25, 64\right) N(25,64)在不同 ρ \rho ρ下的联合分布.下面三张图展示了 ρ = 0 , 0.5 , − 0.5 \rho=0,0.5,-0.5 ρ=0,0.5,−0.5时对应的概率密度.他们显然是不同的分布.

那么,为什么 ρ \rho ρ不同,分布就不同?书中给出的解释是 ρ \rho ρ刻画了两个分量 X 1 X_1 X1, X 2 X_2 X2的关系,不同的关系导致不同的联合分布.那么,究竟是如何刻画的呢?我认为可以从两个角度考察.
中心点
设
(
X
1
,
X
2
)
\left(X_{1}, X_{2}\right)
(X1,X2)服从二维正态分布
N
(
a
,
b
,
σ
1
2
,
σ
2
2
,
ρ
)
N\left(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)
N(a,b,σ12,σ22,ρ). 在给定
X
1
=
x
1
X_{1}=x_{1}
X1=x1的条件下,
X
2
X_{2}
X2的条件密度函数
f
2
(
x
2
∣
x
1
)
=
1
2
π
σ
2
1
−
ρ
2
⋅
exp
[
−
(
x
2
−
(
b
+
ρ
σ
2
σ
1
−
1
(
x
1
−
a
)
)
)
2
2
(
1
−
ρ
2
)
σ
2
2
]
\begin{aligned} f_{2}\left(x_{2} \mid x_{1}\right)=& \frac{1}{\sqrt{2 \pi} \sigma_{2} \sqrt{1-\rho^{2}}} \\ & \cdot \exp \left[-\frac{\left(x_{2}-\left(b+\rho \sigma_{2} \sigma_{1}^{-1}\left(x_{1}-a\right)\right)\right)^{2}}{2\left(1-\rho^{2}\right) \sigma_{2}^{2}}\right] \end{aligned}
f2(x2∣x1)=2πσ21−ρ21⋅exp[−2(1−ρ2)σ22(x2−(b+ρσ2σ1−1(x1−a)))2]
这正是正态分布
N
(
b
+
ρ
σ
2
σ
1
−
1
(
x
1
−
a
)
,
σ
2
2
(
1
−
ρ
2
)
)
N\left(b+\rho \sigma_{2} \sigma_{1}^{-1}\left(x_{1}-a\right), \sigma_{2}^{2}\left(1-\rho^{2}\right)\right)
N(b+ρσ2σ1−1(x1−a),σ22(1−ρ2))的概率密度函数.
根据这个公式,我们可以推出,若 ρ > 0 \rho>0 ρ>0, 则随着 x 1 x_{1} x1的增加, X 2 X_{2} X2(在 X 1 = x 1 X_{1}=x_{1} X1=x1之下) 的条件分布的中心点 m ( x 1 ) m\left(x_{1}\right) m(x1)随 x 1 x_{1} x1的增加而增加. 可以看出: 这意味着当 x 1 x_{1} x1增加时, X 2 X_{2} X2取大值的可能性增加, 即 X 2 X_{2} X2有随着 X 1 X_{1} X1的增长而增长.若 ρ < 0 \rho<0 ρ<0则情况相反.若 ρ = 0 \rho=0 ρ=0则无关.
回到之前的例子,我们考察 r h o = 0.5 rho=0.5 rho=0.5时, X 1 = 15 , 25 , 35 X_1=15,25,35 X1=15,25,35下 X 2 X_2 X2的条件分布.结果如下.可以看到,随着 x 1 x_1 x1的增加, X 2 X_2 X2的条件分布的中心值不断右移.

集中程度
根据公式 N ( b + ρ σ 2 σ 1 − 1 ( x 1 − a ) , σ 2 2 ( 1 − ρ 2 ) ) N\left(b+\rho \sigma_{2} \sigma_{1}^{-1}\left(x_{1}-a\right), \sigma_{2}^{2}\left(1-\rho^{2}\right)\right) N(b+ρσ2σ1−1(x1−a),σ22(1−ρ2))可知条件分布的参数 σ = σ 2 2 ( 1 − ρ 2 ) \sigma=\sigma_{2}^{2}\left(1-\rho^{2}\right) σ=σ22(1−ρ2).而 σ \sigma σ刻画了数据的集中程度. ∣ σ ∣ |\sigma| ∣σ∣越大,数据越是集中于中心点.
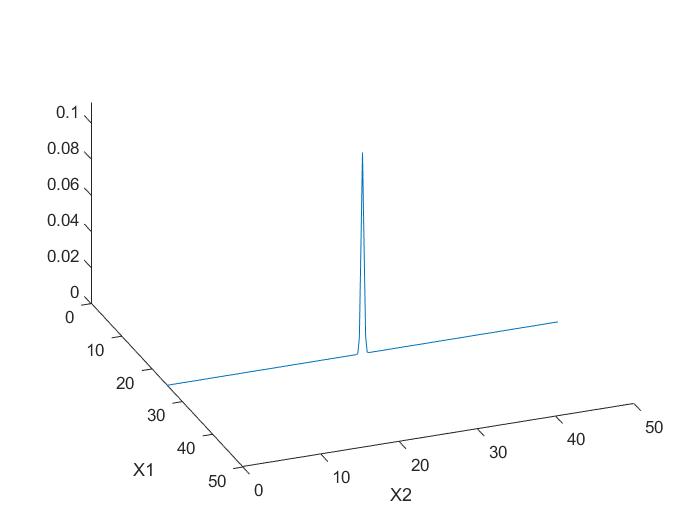
若 ∣ ρ ∣ = 0 |\rho|=0 ∣ρ∣=0,则 σ = σ 2 \sigma=\sigma_2 σ=σ2,说明 X 2 X_2 X2分布的集中程度不受 X 1 X_1 X1影响.现在考虑极端情况,假如 ∣ ρ ∣ = 1 |\rho|=1 ∣ρ∣=1,那么 σ = 0 \sigma=0 σ=0,由一维正态分布的性质可以知道 X 2 X_2 X2的取值全部集中于 m ( X 1 ) m(X_1) m(X1).也就是说, X 2 X_2 X2是 X 1 X_1 X1的函数,其取值由 X 1 X_1 X1完全决定.
下图为
ρ
=
0.999
\rho=0.999
ρ=0.999时
X
2
X_2
X2的条件分布
























 2061
2061

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








