第三章 多维随机变量及其分布

1 二维随机变量

以上我们只限于讨论一个随机变量的情况，但在实际问题中，对于某些随机试验的结果需要同时用两个或两个以上的随机变量来描述。例如，为了研究某一地区学龄前儿童的发育情况，对这一地区的儿童进行抽查。对于每个儿童都能观察到他的身高H和体重W. 在这里，样本空间S={e}={某地区的全部学龄前儿童}，而H(e)和W(e)是定义在S上的两个随机变量。又如炮弹弹着点的位置需要由它的横坐标和纵坐标来确定，而横坐标和纵坐标是定义在同一个样本空间的两个随机变量。

一般，设E是一个随机试验，它的样本空间是S={e}，设X=X(e)和Y=Y(e)是定义在S上的随机变量，由它们构成的一个向量(X,Y)，叫做二维随机向量或二维随机变量（如图3-1）。第二章讨论的随机变量也叫做一维随机变量。

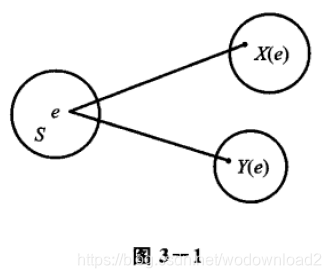
二维随机变量(X,Y)的性质不仅与X及Y有关，而且还依赖于这两个随机变量的相互关系。因此，逐个地来研究X或Y的性质是不够的，还需将(X,Y)作为一个整体来进行研究。

和一维的情况类似，我们也借助“分布函数”来研究二维随机变量。

定义：设(X,Y)是二维随机变量，对于任意实数x,y，二元函数：

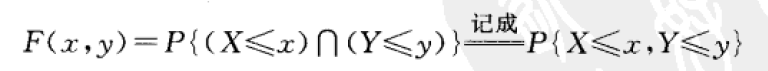
称为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数。

如果将二维随机变量(X,Y)看成是平面上随机点的坐标，那么，分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在如图3-2所示的，以点(x,y)为顶点而位于该点左下方的无穷矩形域内的概率。

依照上述解释，借助于图3-3容易算出随机点(X,Y)落在矩形域{(x,y)|x1<x<=x2, y1<y<=y2}的概率为：

分布函数F(x,y)具有以下的基本性质：

1. F(x,y)是变量x和y的不减函数，即对于任意固定的y，当x2>x1时，F(x2,y)>=F(x1,y)；对于任意固定的x，当y2>y1时，F(x,y2)>=F(x,y1).
2. 0<=F(x,y)<=1，且
   对于任意固定的y，F(-∞,y)=0,
   对于任意固定的x，F(x,-∞)=0，
   F(-∞,-∞)=0，F(∞,∞)=1

上面四个式子可以从几何上加以说明。例如，在图3-2中将无穷矩形的右面边界向左无限平移（即x→-∞），则“随机点（X,Y）落在矩形内”这一事件趋于不可能事件，故其概率趋于0，即有F(-∞,y)=0；又如当x→∞，y→∞时图3-2中的无穷矩形扩展到全平面，随机点（X,Y）落在其中这一事件趋于必然事件，故其概率趋于1，即F（∞,∞）=1。

3. F(x+0,y)=F(x,y)，F(x,y+0)=F(x,y)，即F(x,y)关于x右连续，关于y也右连续。
4. 对于任意(x1,y1)，(x2,y2)，x1<x2，y1<y2，下述不等式成立：
   F(x2,y2)-F(x2,y1)+F(x1,y1)-F(x1,y2)>=0.
   这一性质由(1.1)式及概率的非负性即可得。

如果二维随机变量（X,Y）全部可能取到的值是有限对或可列无限多对，则称（X,Y）是离散型的随机变量。

设二维离散型随机变量（X,Y）所有可能取的值为（xi,yj）,i,j=1,2,…,记P{X=xi,Y=yj}=pij，i,j=1,2,…,则由概率的定义有

我们称P{X=xi, Y=yj}=pij，i,j=1,2,…为二维离散型随机变量（X,Y）的分布律，或随机变量X和Y的联合分布律。
我们也能用表格来表示X和Y的联合分布律，如下表所示。

例1：设随机变量X在1,2,3,4四个整数中等可能地取一个值，另一个随机变量Y在1~X中等可能地取一整数值，试求（X,Y）的分布律。
解：由乘法公式容易求得（X，Y）的分布律。易知{X=i,Y=j}的取值情况是：i=1,2,3,4,j取不大于i的正整数，且

于是（X,Y）的分布律为：

将（X,Y）看成一个随机点的坐标，由图3-2知道离散型随机变量X和Y的联合分布函数为：

其中和式是对一切满足xi<=x,yi<=y的i，j来求和的。

与一维随机变量相似，对于二维随机变量（X,Y）的分布函数F(x,y)，如果存在非负的函数f(x,y)使对于任意x，y有：

则称(X,Y)是连续型的二维随机变量，函数f(x,y)称为二维随机变量（X,Y）的概率密度，或称为随机变量X和Y的联合概率密度。

按定义，概率密度f(x,y)具有以下性质：
1、f(x,y)>=0.
2、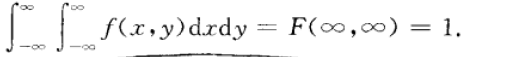
3、设G是xOy平面上的区域，点（X,Y）落在G内的概率为：

4、若f(x,y)在点(x,y)连续，则有

由性质4，在f(x,y)的连续点处有：

在几何上z=f(x,y)表示空间的一个曲面，由性质2知，介于它和xOy平面的空间区域的体积为1。由性质3，P{(X,Y)属于G}的值等于以G为底，以曲面z=f(x,y)为顶面的柱体体积。

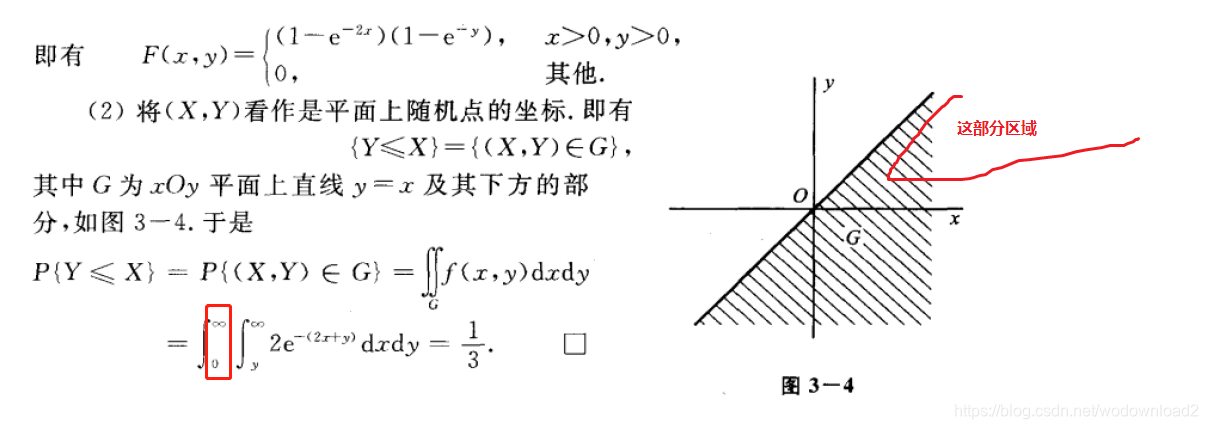
因为f(x,y)在x>0,y>0的概率密度函数不为0，其他为0。

2 边缘分布

二维随机变量(X,Y)作为一个整体，具有分布函数F(x,y)。而X和Y都是随机变量，各自也有分布函数，将它们分别记为Fx(X)，Fy(y)，依次称为二维随机变量（X,Y）关于X和关于Y的边缘分布函数。边缘分布函数可以由（X,Y）的分布函数F(x,y)所确定，事实上，

就是说，只要在函数F(x,y)中令y→∞就能得到Fx(x)。同理Fy(y)=F(∞,y).

对于离散型随机变量，由(1.2)、(2.1)式可得

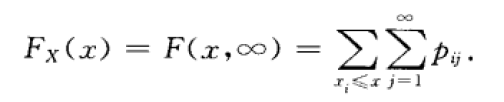
第二章(3.2)式比较，知道X的分布律为：

同样，Y的分布律为：

记：

分别称 pi. (i=1,2,…)和p.j (j=1,2,…)为(X,Y)关于X和Y的边缘分布律（注意，记号pi.中的"."表示pi. 是由pij关于j求和后得到的；同样，p.j是由pij关于i求和后得到的）。

对于连续型随机变量（X,Y），设它的概率密度为f(x,y)，由于

由第二章（4.1）式知道，X是一个连续型随机变量，且其概率密度为：

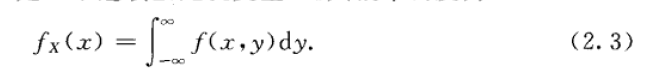
同样，Y也是一个连续型随机变量，其概率密度为：

分布称fx(x)，fy(y)为（X,Y）关于X和Y的边缘概率密度。

例1 一整数N等可能地在1,2,3，…，10个值中取一个值。设D=D(N)是能整除N的正整数的个数，F=F(N)是能整除N的素数的个数（注意1不是素数）。试写出D和F的联合分布律。并求边缘分布律。

解：先将试验的样本空间及D，F取值的情况列出如下：

D所有可能取的值为1,2,3,4; F所有可能取的值为0,1,2. 容易得到(D,F)取（i,j）,i=1,2,3,4,j=0,1,2的概率，例如：

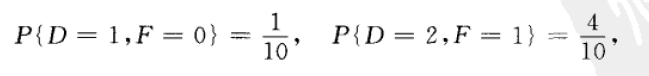
可得D和F的联合分布律及边缘分布律如下表所示：

即有边缘分布律：

我们常常将边缘分布律写在联合分布律表格的边缘上如上表所示。这就是“边缘分布律”这个名词的来源。

例2 设随机变量X和Y具有联合概率密度（图3-5）


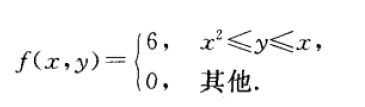
求边缘概率密度fx(x), fy(y).
解：

例3 设二维随机变量（X,Y）的概率密度为：
其中u1,u2,σ1,σ2,ρ都是常数，且σ1>0,σ2>0,-1<ρ<1。我们称(X,Y)为服从参数为u1,u2,σ1,σ2,ρ的二维正态分布（这五个参数的意义将在下一章说明），记为
试求二维正态随机变量的边缘概率密度。

这里补充说明下：

剩下的就是自己简化公式了。

我们看到二维正态分布的两个边缘分布都是一维正态分布，并且都不依赖于参数ρ，亦即对于给定的u1,u2,σ1,σ2，不同的ρ对应不同的二维正态分布，它们的边缘分布却都是一样的。这一事实表明，单由关于X和关于Y的边缘分布，一般来说是不能确定随机变量X和Y的联合分布的。

3 条件分布

我们由条件概率很自然地引出条件概率分布的概念。
设(X,Y)是二维离散型随机变量，其分布律为

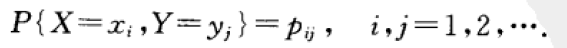
（X,Y）关于X和关于Y的边缘分布律分别为：

设p.j>0，我们来考虑在事件{Y=yj}已发生的条件下事件{X=xi}发生的概率，也就是来求事件

的概率。由条件概率公式，可得：

易知上述条件概率具有分布律的性质：

于是我们引入以下的定义。
定义：设（X,Y）是二维离散型随机变量，对于固定的j，若P{Y=yj}>0，则称

为在Y=yj，条件下随机变量X的条件分布律。

同样，对于固定的i，若P{X=xi}>0，则称：

为在X=xi条件下随机变量Y的条件分布律。

例1 在一汽车工厂中，一辆汽车有两道工序是由机器人完成的。其一紧固3只螺栓，其二是焊接2处焊点。以X表示由机器人紧固的螺栓紧固的不良的数目，以Y表示由机器人焊接的数目。据积累的资料知(X,Y)具有分布律。

（1）求在X=1的条件下，Y的条件分布律；
（2）求在Y=0的条件下，X的条件分布律；

解：边缘分布律已经求出列在上表中。在X=1的条件下，Y的条件分布律为：



例2 一射手进行射击，击中目标的概率为p(0<p<1)，射击直至击中目标两次为止。设以X表示首次击中目标所进行的射击次数，以Y表示总共进行的射击次数，试求X和Y的联合分布律及条件分布律。

相互独立的随机变量

本节我们将利用两个事件相互独立的概念引出两个随机变量相互独立的概念，这是一个十分重要的概念。
定义：设F(x,y)及Fx(x),Fy(y)分别是二维随机变量（X,Y）的分布函数及边缘分布函数。若对于所有x，y有：

则称随机变量X和Y是相互独立的。

设（X,Y）是连续型随机变量，f(x,y)，fx(x)，fy(y)分别为（X,Y）的概率密度和边缘概率密度，则X和Y相互独立的条件(4.2)等价于：等式：

在平面上几乎处处成立。

当（X,Y）是离散型随机变量时，X和Y相互独立的条件（4.2）式等价于：对于（X,Y）的所有可能取的值（xi,yj）有：

在实际中使用(4.3)式或(4.4)式要比使用(4.2)式方便。

例如第一节，例2中的随机变量X和Y，由于：

故有 f(x,y)=fx(x)fy(y)，因而X,Y是相互独立的。

下面考察二维正态随机变量（X,Y），它的概率密度为：

由第2节中的例3知道，其边缘概率密度fx(x)，fy(y)的乘积为：

两个随机变量的函数的分布

上一章5 中已经讨论过一个随机变量的函数的分布，本节讨论两个随机变量的函数的分布。我们只就下面几个具体的函数来讨论。

（一）Z=X+Y的分布
设(X,Y)是二维连续随机变量，它具有概率密度f(x,y)。则Z=X+Y仍为连续型随机变量，其概率密度为