一.回溯法(深度优先搜索)
1.剪枝函数
- 约束函数 --> 剪去不符合条件的分支
- 限界函数 --> 剪去得不到最优解的分支
2. 蒙特卡罗算法
简单来说，就是通过随机抽样，大量统计，得到一个相较精准的结果。
简单应用
例题：
- 蒙特卡洛法计算函数在[a,b]的定积分，选取矩形区域高为c，函数下方区域点数为N,整个矩形区域点数为T，请给出积分值的公式。
- 蒙特卡洛法计算圆周率π。
求解的个数
n皇后求解的个数:
两种状态空间树:
- 排序树 --> n个元素满足某排列 共n!个叶子节点
- 子集树 --> 满足某种性质的子集 2^n个叶子节点
3. n皇后问题
不可以放在一行，一列，同一对角线上
代码：
4.图着色，哈密顿环
图着色:把挨着的色块号都连上
哈密顿环:把图上的每个结点均只遍历一次就可以形成闭环，就是哈密顿环
5.01背包
生成一个结果向量<0,0,1> --> 代表1,2物品不装，3物品装。
- 约束：物品不超重
- 限界：展开后小于当前最大价值
(右结点一定能生成，所以要判断是否生成左子结点）
生成树：
代码：
6.装载问题
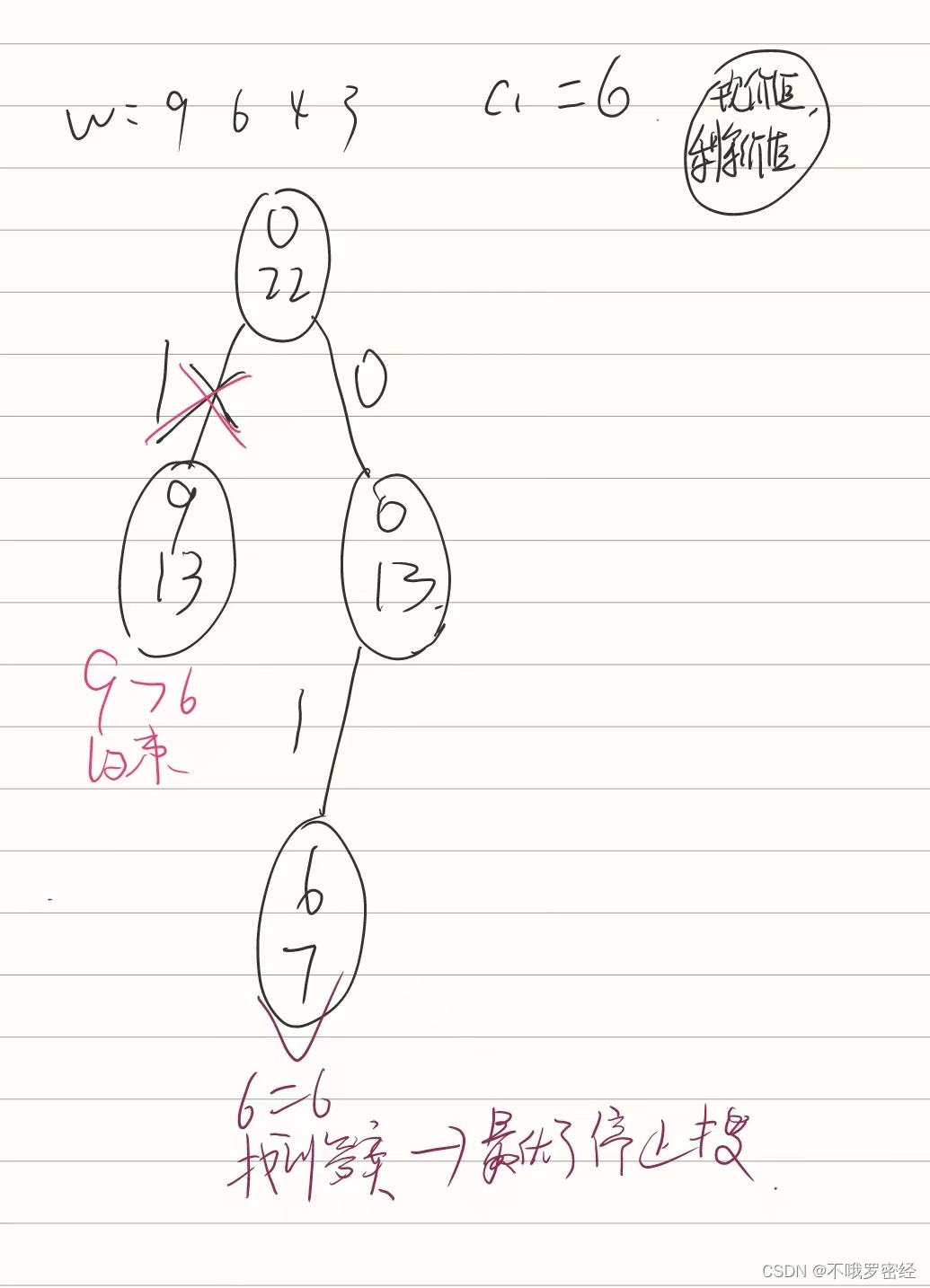
4个物品，重w：9 6 4 3，第一艘船载c1=6.写出回溯法的约束函数与限界函数，并画出解空间树的搜索过程。
- 约束函数 --> 物品不超重 当前物品总重量>船容量
- 限界函数 --> 现在的选择得到的价值加上剩余价值小于当前最大价值
生成树：
代码：
void backtrack (int i)
{//搜索第i层结点
if(i>n)//到达叶结点更新最优解bestx,bestw,return;
if(cw+w[i]<=c)//搜索左子树
r-=w[i];
x[i]=1;
cw+=w[i];
backtrack(i+1);
cw-=w[i];
r+=w[i]
if(cw+r-w[i]>bestw)/搜索右子树
r-=w[i];
x[i]=0;
backtrack(i+1);
r+=w[i];
}7.全排列
生成树：
伪代码：
if (已选择列表的长度 == 元素列表长度)
得到一个全排列
for 元素 in 元素列表
判断元素是否在可选列表
# 做选择 标志为1-->代表不可选
已选列表.add(元素)
backTrace(元素列表, 已选择列表)
# 撤销选择 标志恢复为0-->代表可选
已选列表.remove(元素) -->删除现在的元素，以后add在这个位置上
8.批处理作业调度(最优调度)
回溯法之批处理作业调度 - Thoughtful_z - 博客园 (cnblogs.com)
9.货郎问题
10.回溯算法的效率都与哪些因素有关
- (1)产生x[k]的时间；
- (2)满足显约束的x[k]值的个数
- (3)计算约束函数constraint的时间
- (4)计算限界函数bound的时间；
- (5)满足约束函数和限界函数约束的所有x[k]的个数。 好的剪枝函数能显著地减少所生成的结点数。但这样的剪枝函数往往计算量较大。因此，需要权衡(3)(4)跟(5)
- 回溯法的时间复杂度往往是指数级的。
二.分支限界(广度优先搜索)
1.分支限界法与回溯法的不同
- (1)求解目标：回溯法的求解目标是找出解空间树中满足约束条件的所有解(或一个最优解),而分支限界法的求解目标则是找出满足约束条件的一个解(或最优解)。
- (2)搜索方式的不同：回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
2.01背包
3.装载问题
队列式分支限界法
优先队列式分支限界法
当叶节点的优先级最高时，说明得到了最优解。
4.比较回溯与分支限界的异同点
1845
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
